立体匹配学习笔记3-step1代价计算

代价计算和代价聚合占据了立体匹配效果的7.8成江山啊！！所以很关键！

代价计算：

在代价计算前，我们通过极线矫正使得，代价计算的搜索范围从一张M ✖ N的图变为一个1 ✖ D的向量。如图1所示，D为视差范围，也就是图1右侧的红色长条的长度，x+dmax-x = dmax。

图1，Reference(R)为左视图，Target(T)为右视图

立体匹配算法的四个步骤中的代价聚合该如何理解？ - 知乎 (zhihu.com)图片来源： 立体匹配算法的四个步骤中的代价聚合该如何理解？ - 知乎 (zhihu.com)

代价计算方法有：

1. 平方差 Squared Differences （SD）也就是像素点之间灰度值差的平方。

参考图1对照着看哦，式子中的d是一个范围哦，d∈[0,dmax].

AD算法是基于单个像素点计算的匹配代价，受光照不均、图像噪声影响较大，但对纹理丰富区域有较好的匹配效果。

2. 绝对差 Absolute Differences （AD）灰度值差的绝对值

上面两种并不稳定，易受到噪声的干扰，一个像素点的鲁棒性相当低，和上面的效果和适用范围差不多。

 3. 截断绝对差Truncated Absolute Differences (TAD）

设置了一个条件，将绝对差限制在<=T的条件下，也不是很稳定~因为T需要自己设置。

因为！单个像素的鲁棒性极差更好的方式是通过计算所关注的像素点的邻域的整体情况，来提升信噪比，减少噪声的影响~所以出现了扩大代价计算范围的方法，以IR（x,y）像素为核心向外扩张。

第4点相当于是单个像素到矩阵的过渡↓。

4. Birchfield and Tomasi （BT），主要利用了IR（x,y）与IR（x-1/2,y）之间的亚像素

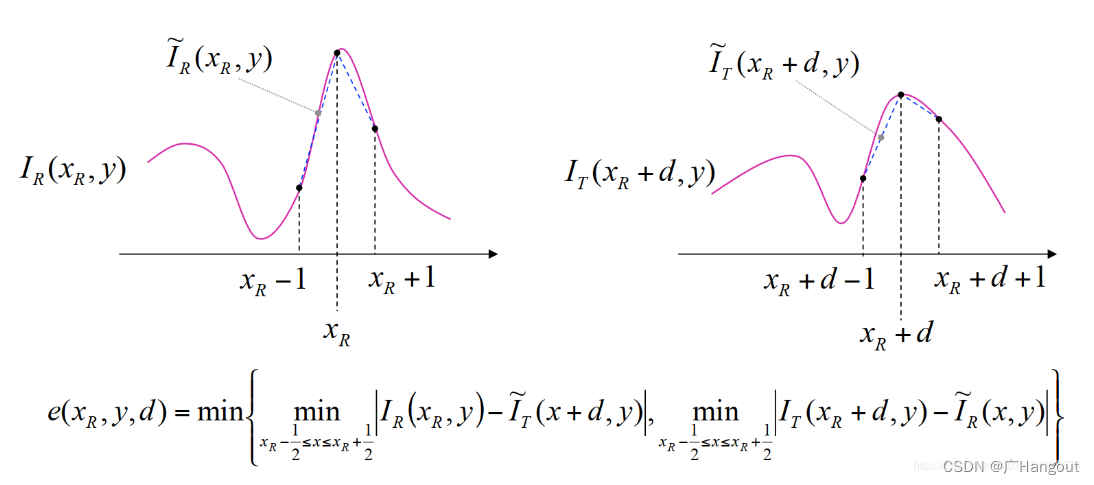
详细的原理可以看这篇： (69条消息) OpenCV中SGBM中BT代价计算_Tomorrow_Maple的博客-CSDN博客

 或者可以直接查文献。

接下来的都是矩阵之间的比较了~

5.Sum of absolute differences（SAD）

图2

 如图2所示，里面的绿色网格就是像素的邻域范围了，也被称为支持窗（Support Window），类似于卷积一样，两个支持窗=两个矩阵，矩阵的绝对差之和就是中心像素的代价了。

这个式子中的IR（x,y）和IT()都是矩阵，d表示视差范围，也就是比较的范围，同一行，不同列。

6.像素差值平方和Sum of Squared differences (SSD)以及像素差值平方和Sum of Squared differences (SSD)  同理

7.Cencus Transform（CT）

其主要思想是，分别对左右视图定义一个相同支持窗,例如[3x3]大小的八邻域。这个支持窗的作用是，让除了中心像素的其他邻域像素与中心像素进行比较。大于中心像素的记作1，小于等于记作0。然后将该邻域按顺时针(自己定义展开规则)展开为二进制码流（一维向量），记录在该中心像素处。

例如:左：[1 2 3;4 5 6;7 8 9]可转为[0 0 0 1 1 1 1 0]；

        右：[2 4 5;6 3 1;1 2 7]可转为[0 1 1 0 1 0 0 1]；

根据Hamming距离，也就是找码流的不同个数、上面的Hamming距离为6；

AD和SAD算法都对光照较为敏感，但Cencus变换则对图片的明暗变化并不敏感，因为Cencus算法是比较的相对灰度关系，所以即使左右影像亮度不一致，也能得到较好的匹配效果，因此它能够较好地检测出图像中的局部结构特征，如边缘、角点特征等。但是Cencus变换对重复区域的匹配效果不好。

因此可以将AD与CT结合 组成AD-Cencus算法。

双目立体匹配之匹配代价计算-云社区-华为云 (huaweicloud.com)

8.互信息Mutual Information（MI）被用于经典的SGM半全局匹配算法。

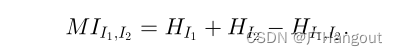
 上面公式为MI的计算公式，HI1和HI2分别为左右视图的熵等同于下面的H(X),H(Y)，HI1I2为两幅图的联合熵同于下面的H(X,Y)。

如果直接看文献中描述的MI代价计算，有点懵逼，，怎么一会儿是积分，然后又用泰勒展开，然后怎么后面又变啦~主要原因还是因为，MI在图像中熵(entropy)的表达方式原因。

这个H（X）描述的就是单个图像中熵的计算公式 。在

 其中，hi表示图像Y中灰度值为i的像素点总数（i∈[0,255]），N表示图像Y的灰度级数。显然Pi表示灰度i出现的概率，于是很自然的就会想到用灰度直方图来计算。matlab中可以用imhist()获得灰度直方图，也可以用entropy()直接获得单幅图的熵。

除了单幅图的熵外，MI还需要两幅图之间的联合熵，联合熵反映了图像X、Y的相关性。

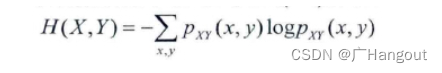
其中，Pxy(x,y)表示左图灰度值为x，同时右图灰度值为y时出现的概率。其联合的灰度直方图不再是2维的，而是3维的。 x轴和y轴分别代表左右图的灰度值，z轴代表该灰度值的累计数量。

MI值越大！相关性越大，联合熵HXY就越小！两幅图就越接近！

但是也出现了一个问题~这个MI值只是一个值，他的大小无从比较，到底多少算大，多少算小？

并且当模板与源图中的多个子图具有相似的灰度分布式，互信息容易出现误匹配的情况；互信息对两幅图像之间的重叠区域比较敏感，如果两幅图像的重叠区太小，互信息就会很小，配准精度随之降低。

所以提出了归一化互信息（Normalization Mutual Information，NMI）和熵相关系数（Entropy Corrleation Coefficient，ECC）

其中H(R)和H(F)分别为左视图和右视图的熵。Reference(R)为左视图，Target(T)为右视图。

[1]Heiko H. Stereo processing by semiglobal matching and mutual information.[J]. IEEE transactions on pattern analysis and machine intelligence,2008,30(2).

下面这篇文章有着MI，NMI，ECC的matlab复现的代码。

(69条消息) 【图像配准】基于互信息的图像配准算法：MI、EMI、ECC算法_qq_34057694的博客-CSDN博客

9.归一化互相关性（Normalized cross correlation，NCC）。

和MI一样~也是两幅图之间的比较。

注意：MI和NCC的图可大可小，因此在局部匹配时，是以某个像素为中心的支持窗为匹配的图像。

除数为两个

若NCC = −1则表示两个匹配窗口完全不相关，相反，若NCC=1时，表示两个匹配窗口相关程度非常高。

 来自链接：(70条消息) python计算机视觉——立体匹配与NCC算法_ncc立体匹配_-pufferflip的博客-CSDN博客