双曲线和直线联立公式_齐次化联立的进阶技巧

废柴的高三学生趁着寒假写第一篇文章...

齐次化联立是一种解决斜率定点问题的方法，但通过知乎上其他文章发现其有较多限制。笔者通过一点点研究将这种方法稍微一般化了一下，成功消除了一部分限制，然后发现大多数的这类问题都可以用此方法解决。

笔者学习这种方法首先是看了 @Dylaaan 大佬的一篇文章

Dylaaan：【解析几何】双联立（齐次化处理）解决定点问题​zhuanlan.zhihu.com

（本文是在这篇文章的基础上写的，建议没了解过这种方法的同学食用前先看一下Dylan的文章）

文章里用了齐次化联立后，相较于常规的联立+韦达定理直接计算，减少了很多计算量。但事实上对于这一类题，文章给出的例题本身就是计算量偏小的题目。

下面是一点对此方法的推广。Dylan在文末中提到一道计算量很大的题目，笔者也成功找出了齐次化联立解决的方法，而且计算量比常规计算小很多（应该吧，笔者太菜导致常规计算没算出来TAT，只能找奇技淫巧）下面也会提到。

刚看完后觉得很有意思，二次方程一消项，就变成了一次方程，从而得到对应的直线方程，很快能找出定点。

然后笔者就找了几道作业题想试一下，结果发现

根本消不掉！

于是就深入研究了一下这种方法。

---

先来描述一下这类问题：过圆锥曲线

上的一点

作两条直线

和

，两条直线的斜率

和

存在某种等量关系（和或积为某定值），两条直线又分别与

有另外两个交点

,

，则直线

过定点。

齐次化联立就是让两条直线合起来写为一个二次方程，让这个二次方程与圆锥曲线方程联立，所得到的方程再通过消项变为一次方程。只要这个消项过程中没有消去 点

或点

对应的解，所得到的一次方程也就仍然满足

的坐标。再由“两点确定一条直线”知所得一次方程即为直线

的方程。最后根据方程中的参数，整理后写为过定点的直线系方程即可求出定点。

在Dylan的文章中，最开始取的这个点

都是椭圆的顶点。而我们在平常做题时会发现，即使点

不是顶点，得到的直线

仍然是过定点的。但如果进行相同操作，会发现会有一次项和常数项被剩下来，导致无法进行消项。

但既然都是过定点直线，按理来说就应该有相应的方法来消项变为一次。我们先看一下消项的原理。

齐次化联立的第一步是把两条直线相乘得到双直线方程

。沿用上面的符号，由于一条直线与圆锥曲线（未退化）至多有两个交点，故这里

和

的所有交点即

,

和

。联立

和

所得到的方程应该能代入这三个点的坐标。而目标方程是直线

的方程，因此就需要消去点

的坐标对应的式子。

明白这一点后就可以有目的地处理方程，从而转化为直线方程。

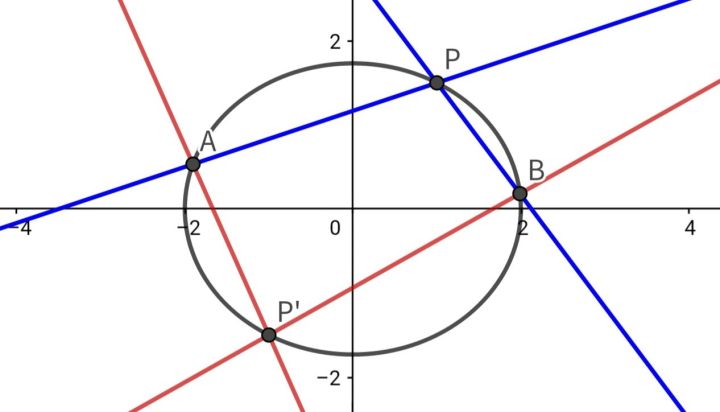
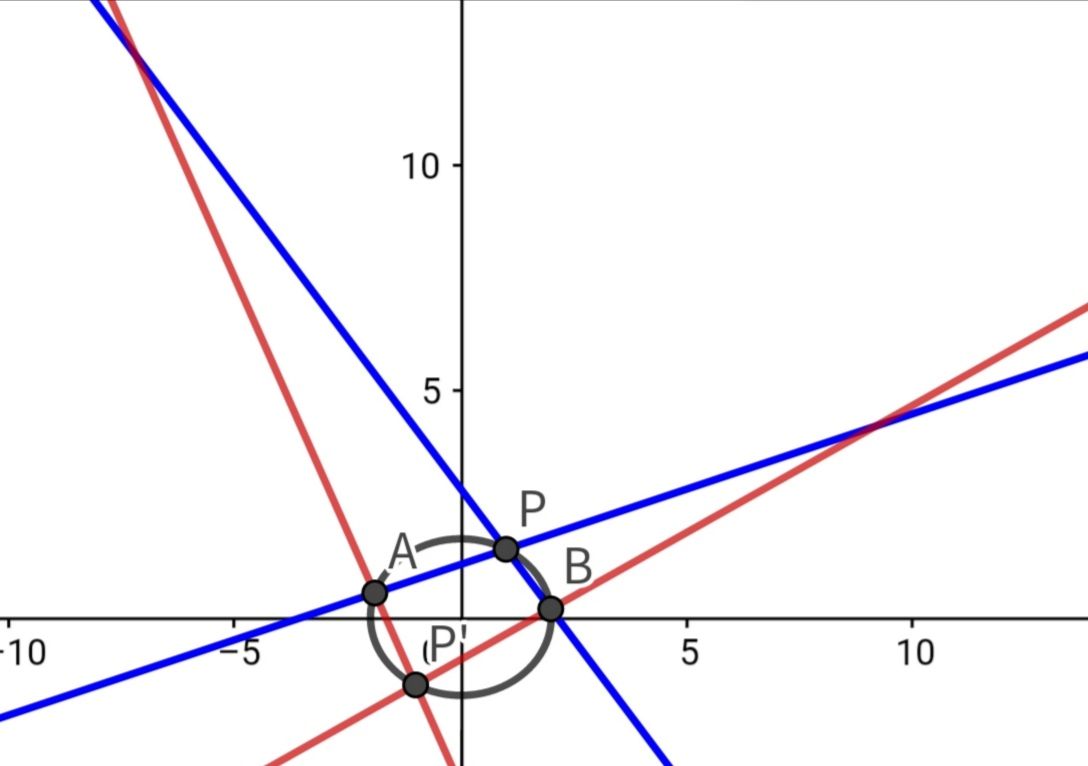
可以随手编一个例题来看一下

椭圆

上有一点

，

,

为

上的两点，直线

和直线

的斜率

满足

.求证：直线

过定点，并求出定点坐标。

首先得出直线

和

的方程分别为

和

相乘得到

但这里我们发现，不管是前面的

还是后面的

都带有一次项。由于椭圆方程不含一次项，导致无法消去一次项，也就无法消去

或是

.

此时我们就需要通过

找到一个关于

和

的关系式

对

简单变形，得到

,也就是

从而有

将其代入

的方程有

两边同乘以

并约去

得到

下面是比较神奇的一步，消去

项。对比这个方程和

当中

的系数我们先把第二项中的

化为

，方程变为

将此方程与双直线方程

相加得

注意到此时

和

的系数之比恰和椭圆方程中一样，故有

和

.代入即可消去所有二次项。整理得

从这里可以看出，

或

为定值时，方程变为直线系方程。对本题，由

得直线方程为

定点坐标解得

,故直线

过定点

。

---

这里需要补充一个引理

我们需要将椭圆和双曲线的第三定义对应的那个性质略作推广一下

椭圆

上一点和左右顶点连线的斜率乘积为定值

，对于双曲线

这一定值为

.

我们可以把左右顶点换为椭圆/双曲线上关于其中心对称的两点，且定值仍然不变。

只需注意到，方程

可以等价变形为

其中

为

上一点。这个方程可以由点差法证出，由于

都是常数，因此这个方程和

是等价的。

---

我们把上面最后与

联立的方程记为

，即

在得到这个方程时，我们消去了

并同乘了

.这意味着消去了点

又引入了

.事实上，这里的

是直线

和直线

所合成的双直线方程。而此时两个双直线的交点就不含点

和点

了。不过它们会有4个交点，其中有两个不在

上，而另外两个就是点

和点

（如下图）.

借助

与

的方程消去

后，由于剩余二次项系数恰成比例，我们也就成功地消去了所有的二次项，从而得到直线

的方程。

这就是最终得到直线方程的原理。虽然

的方程可以由

和

直接合成得到，但考试过程中如果直接引入这么一个对称点

会有点莫名其妙，因此我们可以假装它是由

和

直接联立得到的。

下面我们来写下一般情形，即点

是

上的任意一点时，直线

的方程。

先以椭圆为例。

椭圆

上有一点

.过点

作斜率分别为

的两条直线，各自与

交于另一点，记为点

和点

.则

相乘得

将

写为

，则

代入整理得

两方程相加，得

最后消去二次项，化简得

至此我们成功写出了直线

方程的一般表达式。

对于双曲线推导是类似的，大家可以自己尝试一下，对于双曲线

，其最终结果为

抛物线是无心二次曲线，没法找中心对称点，但对抛物线其实也有相同的结论。

对抛物线

，其他符号同上，一样有

将抛物线方程写为

，代入消去

得

此时，没有

项，直接将仅有的

换掉即得

即所求直线的方程。

最后来说下Dylan提到的难题。

椭圆

，过

作两条直线

、

交椭圆于

四点，两直线斜率满足：

，

和

分别是

和

的中点，求证：直线

过定点。

本题好像和上面的题并不相同，因为定点

并不在椭圆上。但我们应该注意一个东西，设原点为

，则由垂径定理，

,

结合上面对第三定义的推广，这告诉我们，B和C在某个椭圆上。这个椭圆的中心为

的中点，离心率为

.这也就解释了为什么直线

会过定点。

知道轨迹为椭圆只是保证我们能用此方法来求直线方程，如果考场上具体运算时无需说明。我们可以写出这个方程，为

.（考场上可以先说明一下点

和点

在该曲线上）

直线

,

组成的双直线方程为

由上面的椭圆方程得到

代入整理得

椭圆方程中无

项，故仍然要消去

，相加得

由椭圆方程有

.代入消去二次项得

再由

得到直线方程为

故直线

过定点

---

2.18补充一下

前几天在群里发现一些题目的直线不一定过定点，是斜率一定。

不过这种方法还是适用的，以椭圆为例，来看下出现定斜率直线的情形

最终得到的方程为

要定斜率的话，最终的

和

前面的系数就需要成固定比例。

对上式整理出

的系数为

的系数为

若已知

为常数，

为参数，两系数成定比需要

（此时分母为0的情况不符合条件，故不考虑）

注意到

，由合比定理知

或

，即

（舍去）

若

为常数，

为参数，两系数成定比需要

，即

（舍去）

或

，即

因此，当

或

成立时，直线不过定点，但斜率一定

对双曲线，推导是类似的，当

或

成立时，所得直线定斜率

对抛物线则只有

时直线定斜率。

以上推导过程可以无需记住，知道这些结论的作用是在一些题目中快速转化条件，譬如以下的 题。

椭圆

上有一点

.直线

与

交于

，

两点，且满足

.

是坐标原点，求

面积的最大值。(已修改删去第一问)

解：设

,

由

，

组成的双直线方程为

椭圆

的方程变形为

，即

两方程联立得

与

的方程相加得

即

整理后知直线

斜率为定值

.

设

联立

与

的方程得

,

,

故

.当且仅当

时等号成立

本题常规计算的计算量也不算大，但若没找到

斜率为定值

也很难算出来。

相比之下，若是直线过定点但题目中没有提示，常规计算及很不容易发现。下面是16年山东某校的题目（具体哪个学校忘了）.一样的，简单修改删去第一问。

双曲线

上有一点

.过

作两条互相垂直的直线，分别与

交于另两点

，

.求点

到直线

距离的最大值。

解：设

,

则两直线组成的双直线方程为

双曲线方程变形为

,即

与双直线方程联立得

与

的方程相减并代入

得

即

故直线

过定点

.不妨记为点

。

则

。当

，即

时等号成立。此时

，满足条件。

所以点

到直线

距离的最大值为

笔者第一次做到这题时设直线方程爆算，而且完全不知道直线过定点...然后到现在也懒得用常规方法算一遍（