本文是《现代物理有机化学》第七章的笔记，详细阐述了动力学的基础概念，如位能面、反应坐标图、活化络合物的本质。讨论了动态学与动力学的区别，重点介绍了位能面的概念，特别是鞍点在反应过程中的重要性，以及如何通过反应坐标图来理解反应路径和决速步。文章强调了动力学在研究反应机理中的核心地位，并指出动力学图的绘制和理解对于反应动力学研究至关重要。
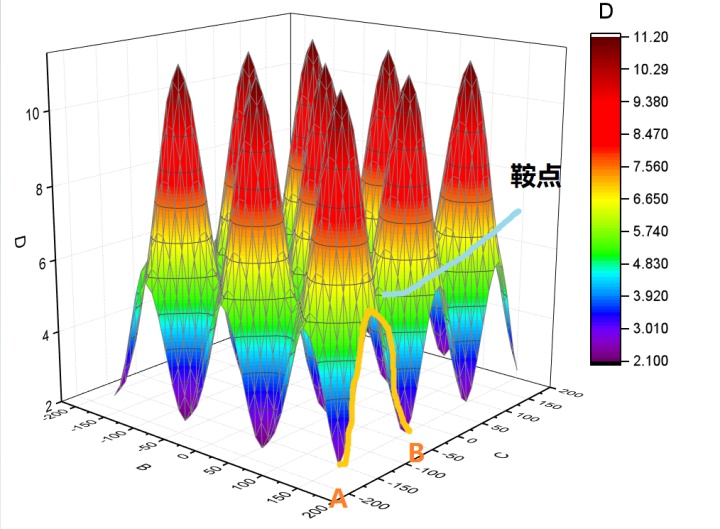
动力学是所有物理有机化学书的重点，它是研究反应机理的工具，本书在讲反应机理之前还是要谈一下动力学的，但是以本书的特点，本章有大量《物理化学》中的动力学内容，作者甚至一二三级反应都要推一遍，这又陷入了“懂的人看得烦，不懂的看了还是不懂”的怪圈。
有机机理中研究最深入的就是SN1，SN2反应，因此本书当然也还是这些例子。本章的重点在于动力学（ kinetics) 和动态学（dynamics)，即理解位能面、深入研究分子运动和碰撞、测定活化参数、测定速率常数、确定某个反应机理中一系列化学步骤的顺序、确定反应限速步或决速步。
作者说在学习完本章之后，读者们应当有能力设计一个动力学研究实验二一通过这个实验，可以得出关于 反应分子性( molecularity)的结论，在得到决速过渡态的基础上洞察始和惰的变化，并表明反应机理中的步骤顺序(即化学反应历程)。
但愿可以吧。本章就是一个机理动力学的归纳，没有刷机理题的乐趣但是也很重要。
重点：在很多基础教材中都会出现上面这种动力学示意图，并把它认为是正常的，本节讲的就是这种图的抽象过程，如何从超曲面到三维图，再到平面图的推导，后来讲了一些动力学基础，并没有什么重要的内容，甚至没什么例子。
7.1 位能面和相关概念
讨论了六章热力学问题，终于进入了动力学的范畴，因为高中化学动力学涉及微分方程讲的少，很多时候容易把热力学的思维带进来。另外，有的物理问题可以用能量守恒解释，也可以用动量计算解释，并不是说有一个解释不本质或者有一个解释更弱，只是角度不一样，能量守恒和动量有重叠部分也有各自擅长的，化学的热力学动力学也是如此。
热力学不讨论中间过程，动力学专门讨论反应中的时间尺度问题。
在我们讲到单个(或一小簇)分子通过一个明确定义的表面时，我们倾向于把这类分析叫做"动态学研究" (dynamics study) 。对真实反应体系宏观测定的讨论，则被称为"动力学"。
动力学最深入人心的概念就是“过渡态理论”和“能垒”，能垒(energy barrier) 这一概念意味着一个(分子在上面进行移动的)能面( surface) ，这个能面的概念使得分子的能量成为其结构的函数(或称应变量)。第二章中我们讨论过势能面的问题，本章将拓展这个概念。
7. 1. 1 位能面
看到这一段有人可能会好奇什么时候讲过，其实是在二面角能量分析的时候，书上没有怎么给图像而已。比如画一个丙烷研究键角和能力的关系，下面左边的二维图就是势能面。
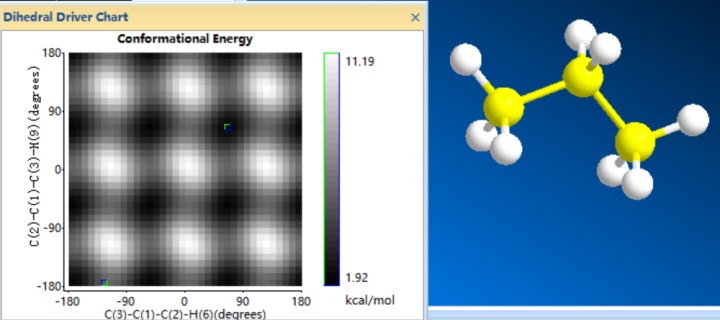
这种图可以画成下面的样子。
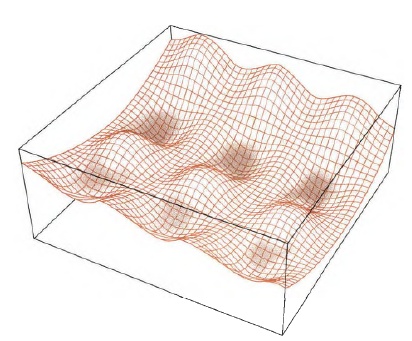
这种图就很明显能看到峰和谷，把他想象成是一个山区的等高图，一般人经过这种地形，大概率是走两个山中间，这就带来一个概念——鞍点(saddle point) 。对上面的丙烷而言，从一个最黑的低能量状态变化到另一个，走经过鞍点的变化花费的能量最少，所以概率最大。（当然能量够是可以爬个山玩一玩的）所以鞍点是研究的重点。
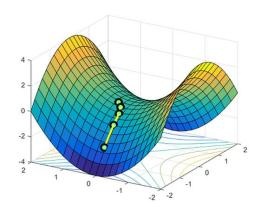
这里要说的是在微分方程中，沿着某一方向是稳定的，另一条方向是不稳定的奇点，叫做鞍点。在泛函中，既不是极大值点也不是极小值点的临界点，叫做鞍点。在矩阵中，一个数在所在行中是最大值，在所在列中是最小值，则被称为鞍点。在物理上要广泛一些，指在一个方向是极大值，另一个方向是极小值的点。这些概念本质上是一样，如此多的地方会涉及鞍点，说明它对过程研究的重要性，比如一些过程优化经常提及鞍点。我们最早接触到的鞍点应该是多元微积分里的鞍点，用偏导数判断极大极小值问题时，
把上面丙烷的图画成下面这样，鞍点的看起来就很明显了。
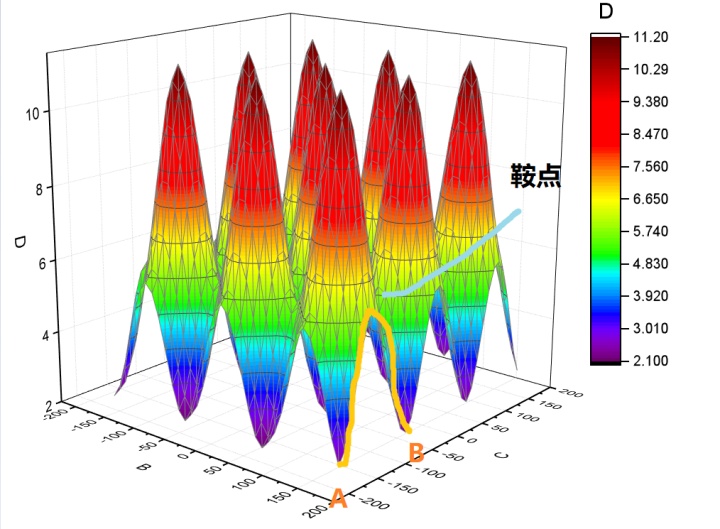
位能面不仅仅是三维的。能量轴只有一个，但是结构坐标处于3N-6 维空间内，其中N 表示分子自由度数。这就是超曲面( hypersurface)，超曲面比较难以在头脑中想象，所以出于方便讨论的目的，一般采用一维或二维几何坐标来表示结构轴(structural axe)，并不是说这种图只能是一维二维。
见上图，当一个反应发生时，分子的内能升高至一个顶点(鞍点)；然后内能随着分子落入相邻的山谷(位能谷〉而下落。在内能面上，与这个能量顶点相关联的分子结构就叫做活化络合物(activated complex) 。在曲线上的物理学意义上的一个点代表了活化络合物的结构，这一个点被叫做过渡态(transition state) 。"活化络合物"和"过渡态"这两个术语尽管从严格意义上来讲是不同的，但是这两个术语还是经常被相互替代使用。经过山的高度被称为反应能垒（barrier to the reaction) 或反应的活化能垒(activation barrier) 。达到过渡态所需的能量大小即为活化能(activation energy) 。
那谁给分子能量让他能“爬山”呢？物理上爬山是动能、内能和重力势能的变化，类似的这里分子获得的也是广义的动能和势能。
大部分化学反应是分子碰撞(参与反应的两个分子之间，或者溶剂分子与反应物之间)的结果。分子碰撞所产生的功能被吸收用于提高分子张力(分子扭曲)。当分子攀升到活化能垒时，它们的平动动能降低;也就是说，由于撞击它们慢了下来，这与台球在撞击时速度慢下来是一样的。与此同时，它们的势能却升高了，具体表现在(由于结构张力或扭曲，或者由于损失自由度所造成的)化学键变弱(见下面)。分子势能的升高可以与其振动模式(如扭转、弯曲、伸展)的激励( excitation) 密切相关。
另外，爬山变化的是高度，分子“爬山”变化的又是什么？z 轴可被最佳理解为以整个反应(包括反应物、中间体、产物、溶剂)的Gibbs 自由能形式表示的势能。但是， z轴也经常被认为是反应物、产物、过渡态、中间体的焓，所以要注意标注的物理量。
分子结构之间的Gibbs 自由能的标准变化可被认为类似于分子间相互转化的驱动力。于是，你会经常听到化学家说起反应的驱动力(driving force for a reaction），即该反应的放能程度(degree of exergonicity) 。比如第三章讲过的，为了降低整个溶液的Gibbs自由能， (溶质和溶剂之间)自发变化成为溶液的过程将会发生。在本章中我们将考虑导致Gibbs 自由能降低的途径，即自发的反应。Gibbs 自由能降低过程中的能垒存在于几乎所有化学反应中，跨越这一能垒的能力与分子的功能有关，因此也与溶液的温度有关。从本质上来讲，为了降低整个溶液的Gibbs 自由能，分子在位能面上到处移动，但是真正能让它们越过能垒的是热运动。
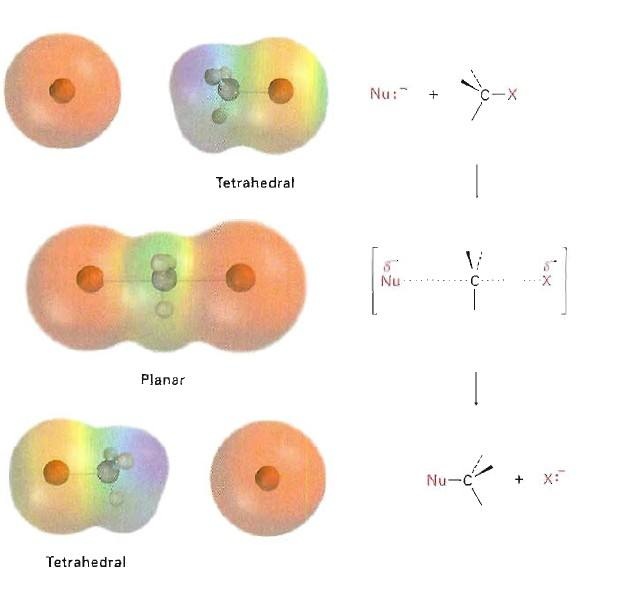
一个问题是很多时候讨论反应过程时只讨论焓，其实熵也有影响。如上图，一个SN2 反应不仅在过渡态中键强较弱，而且由于两个分子相互结合，熵也变得不利。与之相反，对于一个裂解反应来说，熵的增加使得反应(比单一根据键强变化来预测)更有利于进行。这些自由度的变化能够经常支配反应坐标上的Gibbs 自由能。总之，自由度是一个总括一切的术语，指分子所具有的不同运动形式。一个分子拥有越多的自由度，它的熵就越有利。我们会在以后的讨论中显示熵在焓位能面上被指定为位能阱(位能谷)和鞍点的宽度。
与不同的过渡态相关联的入口和出口通道可以有不同的形状。所有这些参数是以下三者的复杂函数:参与化学反应的分子结构、何种分子振动模式随着反应坐标而改变、分子实体有序或无序状态的变化量。
还要注意，上面的位能图中还有另外一维空间没有显示，而且这一维空间在山脉图像中没有相应类比物。这与分子振动状态有关。每个山谷和山埋都有各自相应的梯级，这就意味着能面还包含着许多层的分子振动状态，在每一层中存在着特定一节的分子。因此，真实情况下的位能面并不是如图里画的那么简单。
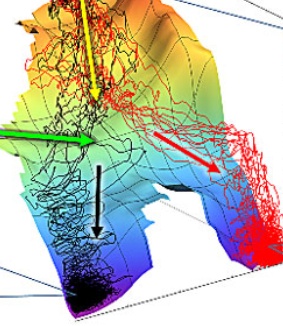
现在我们可以有足够理由说，当分子穿越某一特定能垒时，可以经由许多不同的小道或说是轨迹。根据分子的起始速度或动量，是否处于基态或激发态，目前处于几种构象中的哪一种，分子的各自振动状态等因素，每个分子会经由稍微不同的路径到达产物。这些中的许多路径并不属于绝对最小能量路径。这意味着所有的反应物并不经由某单一化学路径而变成产物，而是经由一组可能的路径。
有统计的思想，没有单一路径意味着我们所观察到的化学反应速率是所有不同可能路径的所有速率的加权平均值。所以动力学图像描绘了一个从理论观点上看来十分困难的场景，因为这里面存在着很多的变量。
为了简化，我们常常专注于从反应物到过技态的最低能量路径，或者代表所有路径加权平均值的一条单一路径。这样，我们可以把动力学图简化到一个可以处理的水平。这就出现了反应坐标图。于是这些反应坐标图表示了在反应机理里分子经由的所有路径的综合图。
当然，和电子不同，反应的分子是可以观察的，现在跟踪单一分子的动力学的技术已经被开发出来，用来考察单一分子的反应坐标，比如说飞秒化学。
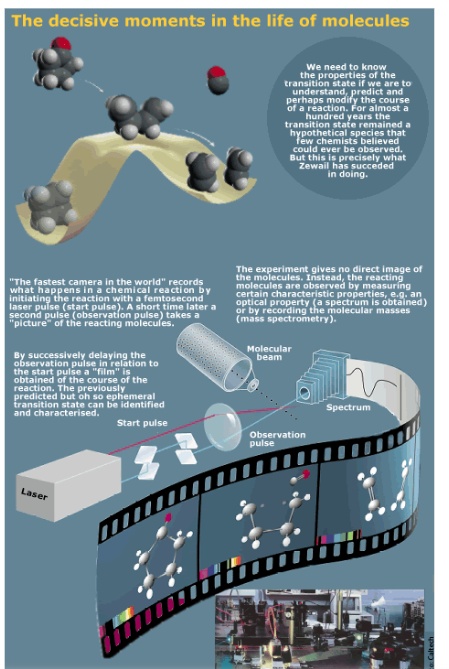
7. 1. 2 反应坐标图
最小能量路径，或者被我们描述为是所有路径的加权平均值的路径，被称为反应坐标。如果以二维图来描绘这一路径(其中一个变量是能量) ，就可以给出反应坐标图。
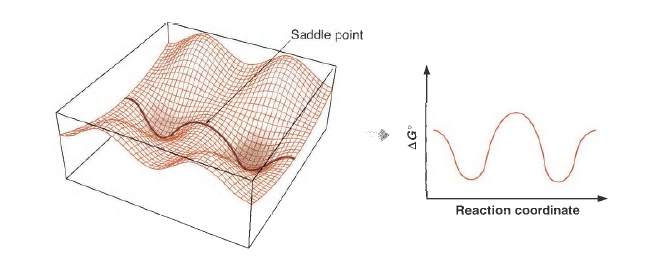
为了画一张反应坐标图，我们专注于其中的截面图，它以单一几何坐标作为x轴，而以能量作为y轴。这种二维图给出了一条表示最小能量路径的曲线，这些图对于定性讨论反应机理非常有用 。过渡态是(反应物与产物相互转换)的最小能量路径中的最高点。
反应坐标图显示了过渡态、稳定结构、瞬时中间体之间的明显区别。在反应坐标图中，一个相对稳定的结构以曲线中一个低能量的沉降(阱)表示，活泼中间体为高能量的浅阱，而过渡态则为峰状。任何存留时间比典型化学键振动时间(10^-14~10^-13s) 还要长的化学结构，就可以被认为是中间体。如果每个阱与阱之间的能垒越大，那么分子结构的存活寿命就越长，这以曲线的下降部分来表示。具体可以看下面这个例子，
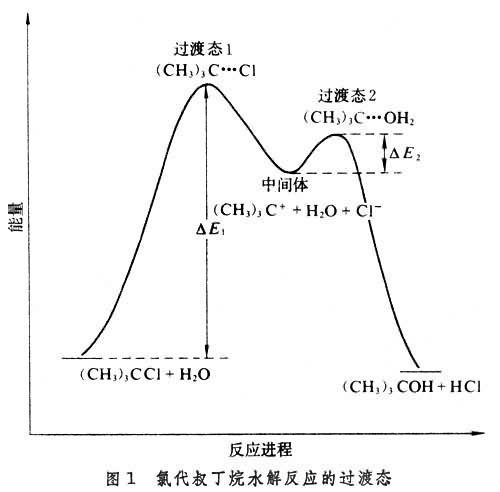
当反应涉及多个中间体就会有涉及到决速步的问题。有时也称限速步，控速步，在某些人的定义中可能三个词有区别，但这里我们认为三者同义。决速步指速率决定着产物形成的整体测得速率的一步，一般表现为最慢的一步，在能量上，一般是能垒最高的反应。但注意，能垒最高不一定是中间态能量最高的。下图中的F就是一个例子，第二步的能垒并不高，决速步是第一步。
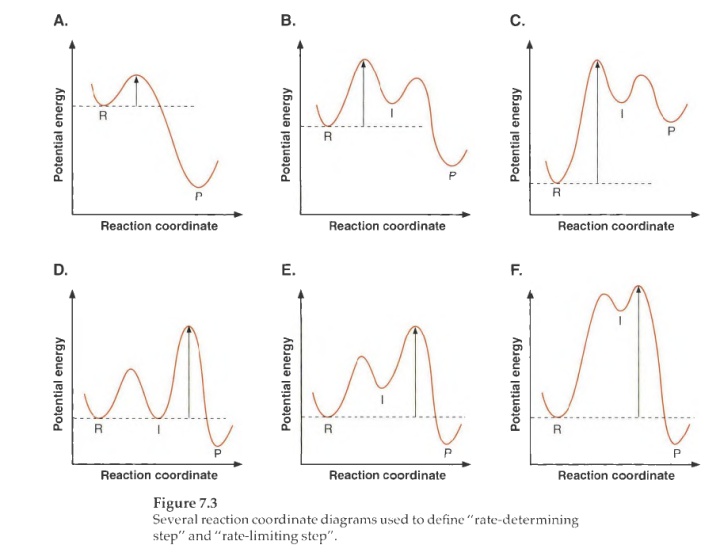
上图中还要注意的D和E，会出现这种中间体变回原料更容易的例子。
上面说了在势能面上“行走”可以有不同的路径，有时反应甚至会改变方向。而根据物理上鞍点的定义“一个方向是极大值，另一个方向是极小值的点”。鞍点是不容易改变方向的，而峰或谷则容易改变方向。又因为谷的能量低，分子停留的时间或者说“寿命”长，一般都是在谷的地方转向的。
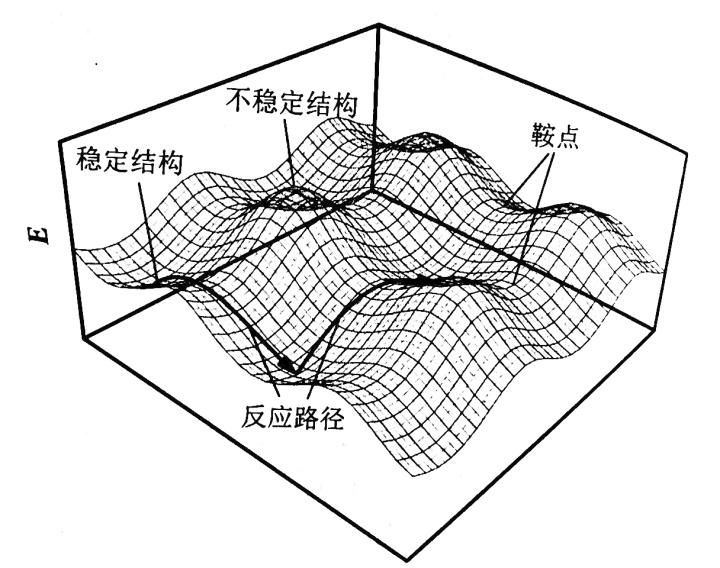
那开头提到平面图（反应坐标图）被化学家第一次勾画时式主要来自于直觉、反应自由能或焓的知识，以及是否存在中间体。
一条用于画复杂反应的反应坐标图的指导原则被叫做最小运动法则(principle of least motion) 。从反应物到产物、或从中间体到另一中间体或产物进行的有利反应，是那些原子核位置或电子构型变化最小的反应。也就是说虽然很多化学反应涉及原子核位置的显著变化，这些变化通常只是通过一些简单的反应而发生的。
当然，直觉不一定可靠，创建反应坐标图的严格方法也是存在的。
7. 1. 3 活化络合物/过渡态的本质
看到这个题目，没错，奇怪的内容要来了，这次不是哲学，不是物理，是数学，因为数学很普及，就不多说了。
活化络合物是指存留时间不长于分子振动时间的分子实体，这意味着存在着某种特定的原子运动使得活化络合物朝向产物或反应物方向移动。正如沿反应坐标上(终点除外)的所有结构一样，活化络合物是一种呈现既有反应物又有产物结构特征的物种。使得过渡态变得非常独特的原因在于它表示了反应坐标上代表化学反应过程中张力最大或不稳定的结构。
回忆第二章最后面的分子力学，那些分析表达式本质上表示一个体系的能量变化
能面上的驻点(stationary point) 是指没有施加作用力的一点。
作用力为一阶导数
书上接下来讲了Hessian 矩阵，这个在各种优化中挺常见的，了解了解也好，下图来自百度百科[1]。
- 简单来说，正定矩阵：矩阵特征值均为正。负定矩阵：矩阵特征值均为负。
- 半正定矩阵： 所有特征值为非负。半负定矩阵：所有特征值为非正。
- 不定矩阵：特征值有正有负。
这个在数学上其实挺好理解的，而且因为经常用在各种优化里，物理科普算法科普经常讲这个概念，看看也无所谓了，虽然我现在还不知道作者这里突然一个“过渡态数学本质”到底想表达什么。
比如
在第2~4 章中我们讨论了在反应热力学上加以数量化(即定量化)的方法。为了给反应坐标图上的峰和谷的相对能量加以数量化，化学家常常转向两种相关方法：过渡态理论(TST) 和Arrhenius 速率定律。速率常数在这两种方法的速率表达式中会被用到，因此我们需要扼要回顾一下速率、速率常数、速率表达式的概念。
7. 1. 4 速率和速率常数
我们规定对于反应 R→P，反应物浓度是[R]，产物浓度是[P]。
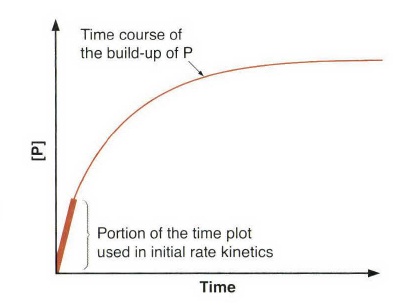
反应速率
从之前的定义我们知道，一个化学反应的速率应该依赖于需要爬越的能垒高度以及温度。在数学上，这种依赖关系可以表达为反应物浓度([R]) 和反应速率之间的一个比例常数，这被称为速率常数。速率常数用字母k来表示，有时写成kn，其中下标n表示反应级数或表示该速率常数是多步反应中哪一步的。
7. 1. 5 反应级数和速率定律
结合"反应速率应当依赖于速率常数和浓度两者"这一逻辑，就可以得出微分速率方程，也称为速率定律(rate law) 。
化学反应的分子性(molecularity) 是指反应过渡态所涉及的分子数目。这一术语只能应用于单步反应，也称为基元反应(elementary reaction) 。如果过渡态只涉及一个分子，那么这一反应就是单分子的。如果有两个分子参与，那么反应就是双分子的。三分子( termolecular) 过程涉及三个分子，这类反应比较少见，但也并不是从没出现过。
SN1，SN2，E1，E2中的1，2就是指单分子反应/双分子反应，他们在动力学方程上表现为反应级数不同。
本节很多补充来自清华的《物理有机化学》，这本书受《现代物理有机化学》一书影响极深，看目录就知道了，不喜欢具体例子和过多哲学思考的，可以翻一翻。
肖暄中：《现代物理有机化学》笔记 第七章（2）过渡态理论zhuanlan.zhihu.com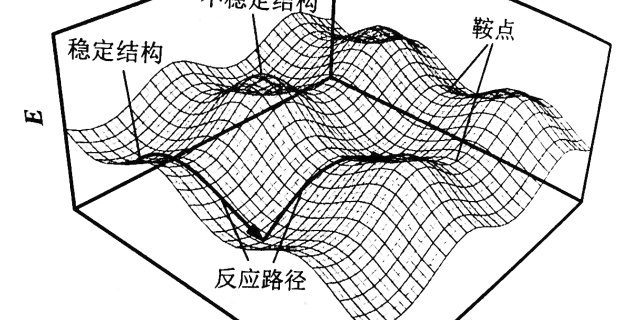
目录：
- 《现代物理有机化学》笔记 第一章 化学键基础（1）
- 《现代物理有机化学》笔记 第二章 张力和稳定性（1）
- 《现代物理有机化学》笔记 第三章 溶液和非共价结合力（1）
- 《现代物理有机化学》笔记 第五章 酸碱（1）
- 《现代物理有机化学》笔记 第六章 立体化学（1）
- 《现代物理有机化学》笔记 第七章 动力学（1）
- 《现代物理有机化学》笔记 第八章 机理相关实验（1）
- 《现代物理有机化学》笔记 第九章 催化（1）
- 《现代物理有机化学》笔记 第十章 机理（1）
- 《现代物理有机化学》笔记 第十一章 机理2（1）
- 《现代物理有机化学》笔记 附录五
参考
- ^https://baike.baidu.com/item/%E9%BB%91%E5%A1%9E%E7%9F%A9%E9%98%B5/2248782?fr=aladdin
扫一扫
3829
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
