二维空间
在二维空间中,旋转可以用一个单一的角$$\theta$$定义。作为约定,正角表示逆时针旋转。把笛卡尔坐标的列向量关于原点逆时针旋转  的矩阵是:
的矩阵是:
三维空间
在三维空间中,旋转矩阵有一个等于单位1的实特征值。旋转矩阵指定关于对应的特征向量的旋转(欧拉旋转定理)。如果旋转角是 θ,则旋转矩阵的另外两个(复数)特征值是 exp(iθ) 和 exp(-iθ)。从而得出 3 维旋转的迹数等于 1 + 2 cos(θ),这可用来快速的计算任何 3 维旋转的旋转角。
3 维旋转矩阵的生成元是三维斜对称矩阵。因为只需要三个实数来指定 3 维斜对称矩阵,得出只用三个是实数就可以指定一个 3 维旋转矩阵。
Roll, Pitch 和 Yaw
生成旋转矩阵的一种简单方式是把它作为三个基本旋转的序列复合。关于右手笛卡尔坐标系的 x-, y- 和 z-轴的旋转分别叫做 pitch, yaw 和 roll 旋转。因为这些旋转被表达为关于一个轴的旋转,它们的生成元很容易表达。
- 绕 x-轴的主动旋转定义为:
-
 这里的
这里的
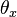 是 roll 角。
是 roll 角。
- 绕 y-轴的主动旋转定义为:
-
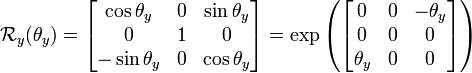 这里的
这里的
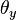 是 pitch 角。
是 pitch 角。
- 绕 z-轴的主动旋转定义为:
-
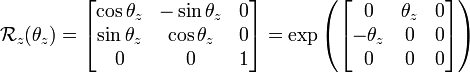 这里的
这里的
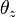 是 yaw 角。
是 yaw 角。
在飞行动力学中,roll, pitch 和 yaw 角通常分别采用符号  ,
,  , 和
, 和  ;但是为了避免混淆于欧拉角这里使用符号
;但是为了避免混淆于欧拉角这里使用符号 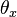 ,
, 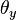 和
和 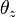 。
。
任何 3 维旋转矩阵 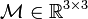 都可以用这三个角
都可以用这三个角 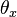 ,
, 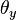 , 和
, 和 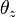 来刻画,并且可以表示为 roll, pitch 和 yaw 矩阵的乘积。
来刻画,并且可以表示为 roll, pitch 和 yaw 矩阵的乘积。
-
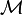 是在
是在
 中的旋转矩阵
中的旋转矩阵

在  中所有旋转的集合,加上复合运算形成了旋转群 SO(3)。这里讨论的矩阵接着提供了这个群的群表示。更高维的情况可参见 Givens旋转。
中所有旋转的集合,加上复合运算形成了旋转群 SO(3)。这里讨论的矩阵接着提供了这个群的群表示。更高维的情况可参见 Givens旋转。
角-轴表示和四元数表示
在三维中,旋转可以通过单一的旋转角  和所围绕的单位向量方向
和所围绕的单位向量方向  来定义。
来定义。
这个旋转可以简单的以生成元来表达:
在运算于向量 r 上的时候,这等价于Rodrigues旋转公式:
角-轴表示密切关联于四元数表示。依据轴和角,四元数可以给出为正规化四元数 Q:
这里的 i, j 和 k 是 Q 的三个虚部。
欧拉角表示
在三维空间中,旋转可以通过三个欧拉角  来定义。有一些可能的欧拉角定义,每个都可以依据 roll, pitch 和 yaw 的复合来表达。依据 "z-x-z" 欧拉角,在右手笛卡尔坐标中的主动旋转矩阵可表达为:
来定义。有一些可能的欧拉角定义,每个都可以依据 roll, pitch 和 yaw 的复合来表达。依据 "z-x-z" 欧拉角,在右手笛卡尔坐标中的主动旋转矩阵可表达为:
进行乘法运算生成:
因为这个旋转矩阵不可以表达为关于一个单一轴的旋转,它的生成元不能像上面例子那样简单表达出来。











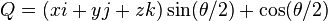
















 517
517











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








