定理:已知三角形△A1A2A3的顶点坐标Ai ( xi , yi ) ( i =1, 2, 3) 。则它的重心坐标为:
xg = (x1+x2+x3) / 3 ;
yg = (y1+y2+y3) / 3 ;
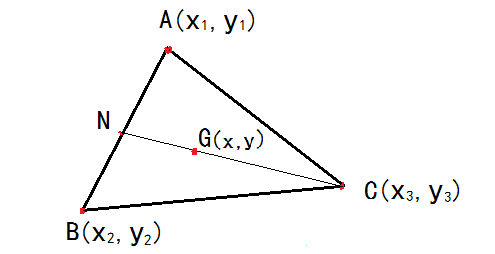
设三点为A(x1.y1)B(x2,y2)C(x3,y3)
重心G点坐标(x,y)
考虑xm
任取两点(不妨设为A和B),则重心G在以AB为底的中线(CN)上.
N点横坐标为(x1+x2)/2
重心G在CN距N点1/3处,即NG=1/3*CN
故重心横坐标为
xm=1/3*(x3-(x1+x2)/2)+(x1+x2)/2
=(x1+x2+x3)/3
同理,ym=(y1+y2+y3)/3























 2253
2253

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








