交互式变形是编辑几何模型的重要手段,目前出现了许多实时、直观的交互式变形方法。本文介绍一种利用线性混合蒙皮(Linear Blending Skinning,LBS)技术来实现网格变形的方法,线性混合蒙皮技术由于计算速度优势使得其成为商业应用中最主要的方法之一。蒙皮算法一般分两步:第一步用户在几何模型上选择一系列控制单元,并计算几何模型受这些控制单元的影响权重;第二步用户拖动控制单元,几何模型随控制单元发生相应变形。第一步中权重的计算决定了蒙皮算法的效果,如果想要几何模型发生自然、高质量的形变,必须得有一种高效准确的权重计算方法。
文章[Jacobson et al. 2011]介绍了一种有界双调和权重(Bounded Biharmonic Weights,BBW)的计算方法,该权重能使得几何模型发生平滑变形。定义控制单元为Hj∈Ω,j = 1, … , m,每个控制单元Hj的仿射变换为Tj,对于顶点p∈Ω,线性混合蒙皮算法给出变形后p’的位置为控制单元仿射变换Tj的加权线性组合:
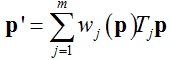
其中wj(p)为顶点p受控制单元Hj的权重影响。
对于有界双调和权重wj的计算方法,其数学表达式如下,最小化问题可以转化为求解对应的Euler-Lagrange方程,即双调和方程Δ2wj= 0,而其同时满足设定的限制条件,因此作者将这种权重命名为有界双调和权重。
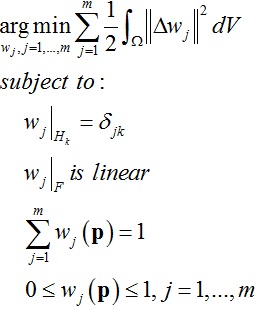









 本文介绍了线性混合蒙皮(LBS)技术在网格变形中的应用,重点讨论了有界双调和权重(BBW)的计算方法,用于实现平滑的几何模型变形。虽然精确的权重计算能避免一些问题,但皮肤塌陷仍然存在。通过对偶四元数的使用,解决了旋转矩阵导致的塌陷问题,能够同时表示空间旋转和平移。参考了Alec Jacobson等人的研究工作,探讨了对偶四元数在变形计算中的作用。
本文介绍了线性混合蒙皮(LBS)技术在网格变形中的应用,重点讨论了有界双调和权重(BBW)的计算方法,用于实现平滑的几何模型变形。虽然精确的权重计算能避免一些问题,但皮肤塌陷仍然存在。通过对偶四元数的使用,解决了旋转矩阵导致的塌陷问题,能够同时表示空间旋转和平移。参考了Alec Jacobson等人的研究工作,探讨了对偶四元数在变形计算中的作用。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








