中兴
之前看了 华为OD 和 小米 的薪资一览表,不少同学表示想看「中兴」相关的薪资爆料。
说到中兴,估计它已经被不少网友淡忘了,但其实中兴在通讯领域的地位仍然是举足轻重。
中兴在全球拥有 8.5W 件专利,光这些专利技术的价值就超过 450 亿人民币。
说起通讯领域,大家又容易想起另一家巨头:华为。
网传他们两家存在某种"不成文"的协议,就是相互不招对方的人,当然现在可能已经转为"成文"的竞业协议了。
扯得有点远,还是来看看「中兴」的职级和薪资吧。
中兴整体有三条职业发展跑道(2P+M),分别是 P(专业)序列、M(管理序列)以及 P(项目序列)。
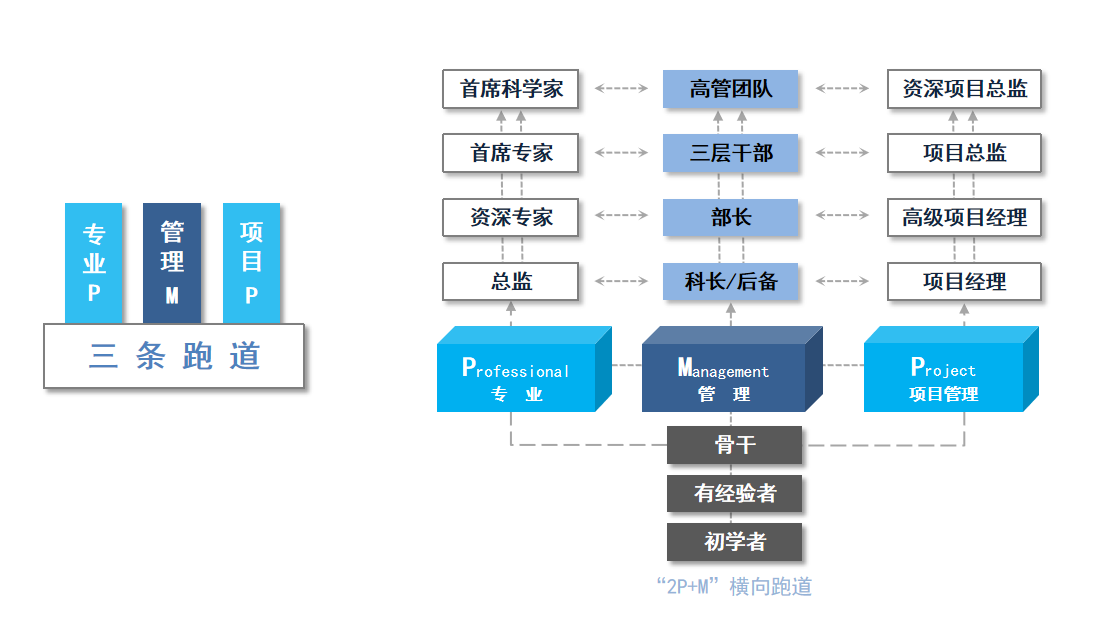
中兴采取 7*3 的职级积分晋升机制,每年两次晋升评级,员工可以通过「绩效贡献、项目贡献、关键事件贡献」三种形式进行积分,达到一定积分即可申请晋级加薪。
更具体的职级,是从1级到7级,7>6>5>4>3>2>1,然后每个级别分ABC,A>B>C。
对应的月薪标准为:
-
1级:6k ~ 9k -
2级:9k ~ 15k -
3级:12k ~ 18k -
4级:15k ~ 20k -
5级:20k ~ 80k -
6级:80k ~ 200k -
7级:200k ~ 500k
至于年终奖待遇,和所在部门关系很大,中位数一般在 2~4 个月。
除了基本薪资和常规的五险一金以外,中兴还会统一为员工提供免费的商业意外保险(出差海外的员工还有免费海外商旅险)、低价食堂、免费班车、通讯费补贴以及低价人才公寓(深圳、南京、三亚)。
对于「中兴」以及薪资,你有什么想说的,欢迎评论区交流。
...
回归主题。
来一道和秋招相关的算法题。
题目描述
平台:LeetCode
题号:74
编写一个高效的算法来判断 m x n 矩阵中,是否存在一个目标值。该矩阵具有如下特性:
-
每行中的整数从左到右按升序排列。 -
每行的第一个整数大于前一行的最后一个整数。
示例 1:
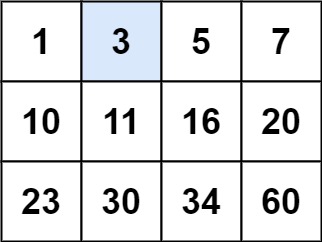
输入:matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
输出:true
示例 2:
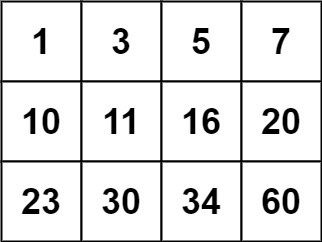
输入:matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
输出:false
提示:
二分(一)
由于二维矩阵固定列的「从上到下」或者固定行的「从左到右」都是升序的。
因此我们可以使用两次二分来定位到目标位置:
-
第一次二分:从第 0 列中的「所有行」开始找,找到合适的行 row -
第二次二分:从 row中「所有列」开始找,找到合适的列col
Java 代码:
class Solution {
public boolean searchMatrix(int[][] mat, int t) {
int m = mat.length, n = mat[0].length;
// 第一次二分:定位到所在行(从上往下,找到最后一个满足 mat[x]][0] <= t 的行号)
int l = 0, r = m - 1;
while (l < r) {
int mid = l + r + 1 >> 1;
if (mat[mid][0] <= t) l = mid;
else r = mid - 1;
}
int row = r;
if (mat[row][0] == t) return true;
if (mat[row][0] > t) return false;
// 第二次二分:从所在行中定位到列(从左到右,找到最后一个满足 mat[row][x] <= t 的列号)
l = 0; r = n - 1;
while (l < r) {
int mid = l + r + 1 >> 1;
if (mat[row][mid] <= t) l = mid;
else r = mid - 1;
}
int col = r;
return mat[row][r] == t;
}
}
C++ 代码:
class Solution {
public:
bool searchMatrix(vector<vector<int>>& mat, int t) {
int m = mat.size(), n = mat[0].size();
// 第一次二分:定位到所在行
int l = 0, r = m - 1;
while (l < r) {
int mid = l + r + 1 >> 1;
if (mat[mid][0] <= t) l = mid;
else r = mid - 1;
}
int row = r;
if (mat[row][0] == t) return true;
if (mat[row][0] > t) return false;
// 第二次二分:从所在行中定位到列
l = 0; r = n - 1;
while (l < r) {
int mid = l + r + 1 >> 1;
if (mat[row][mid] <= t) l = mid;
else r = mid - 1;
}
int col = r;
return mat[row][l] == t;
}
};
Python 代码:
class Solution:
def searchMatrix(self, mat, t):
m, n = len(mat), len(mat[0])
# 第一次二分:定位到所在行
l, r = 0, m - 1
while l < r:
mid = l + r + 1 >> 1
if mat[mid][0] <= t:
l = mid
else:
r = mid - 1
row = r
if mat[row][0] == t:
return True
if mat[row][0] > t:
return False
# 第二次二分:从所在行中定位到列
l, r = 0, n - 1
while l < r:
mid = l + r + 1 >> 1
if mat[row][mid] <= t:
l = mid
else:
r = mid - 1
col = r
return mat[row][l] == t
TypeScript 代码:
function searchMatrix(mat: number[][], t: number): boolean {
const m = mat.length, n = mat[0].length;
// 第一次二分:定位到所在行
let l = 0, r = m - 1;
while (l < r) {
const mid = l + r + 1 >> 1;
if (mat[mid][0] <= t) l = mid;
else r = mid - 1;
}
const row = r;
if (mat[row][0] == t) return true;
if (mat[row][0] > t) return false;
// 第二次二分:从所在行中定位到列
l = 0; r = n - 1;
while (l < r) {
const mid = l + r + 1 >> 1;
if (mat[row][mid] <= t) l = mid;
else r = mid - 1;
}
const col = r;
return mat[row][l] == t;
};
-
时间复杂度: -
空间复杂度:
二分(二)
当然,因为将二维矩阵的行尾和行首连接,也具有单调性。
我们可以将「二维矩阵」当做「一维矩阵」来做。
Java 代码:
class Solution {
public boolean searchMatrix(int[][] mat, int t) {
int m = mat.length, n = mat[0].length;
int l = 0, r = m * n - 1;
while (l < r) {
int mid = l + r + 1 >> 1;
if (mat[mid / n][mid % n] <= t) l = mid;
else r = mid - 1;
}
return mat[r / n][r % n] == t;
}
}
C++ 代码:
class Solution {
public:
bool searchMatrix(vector<vector<int>>& mat, int t) {
int m = mat.size(), n = mat[0].size();
int l = 0, r = m * n - 1;
while (l < r) {
int mid = l + r + 1 >> 1;
if (mat[mid / n][mid % n] <= t) l = mid;
else r = mid - 1;
}
return mat[l / n][l % n] == t;
}
};
Python 代码:
class Solution:
def searchMatrix(self, mat, t):
m, n = len(mat), len(mat[0])
l, r = 0, m * n - 1
while l < r:
mid = l + r + 1 >> 1
if mat[mid // n][mid % n] <= t:
l = mid
else:
r = mid - 1
return mat[l // n][l % n] == t
TypeScript 代码:
function searchMatrix(mat: number[][], t: number): boolean {
const m = mat.length, n = mat[0].length;
let l = 0, r = m * n - 1;
while (l < r) {
const mid = l + r + 1 >> 1;
if (mat[Math.floor(mid / n)][mid % n] <= t) l = mid;
else r = mid - 1;
}
return mat[Math.floor(l / n)][l % n] === t;
};
-
时间复杂度: -
空间复杂度:
抽象 BST
我们可以将二维矩阵抽象成「以右上角为根的 BST」:
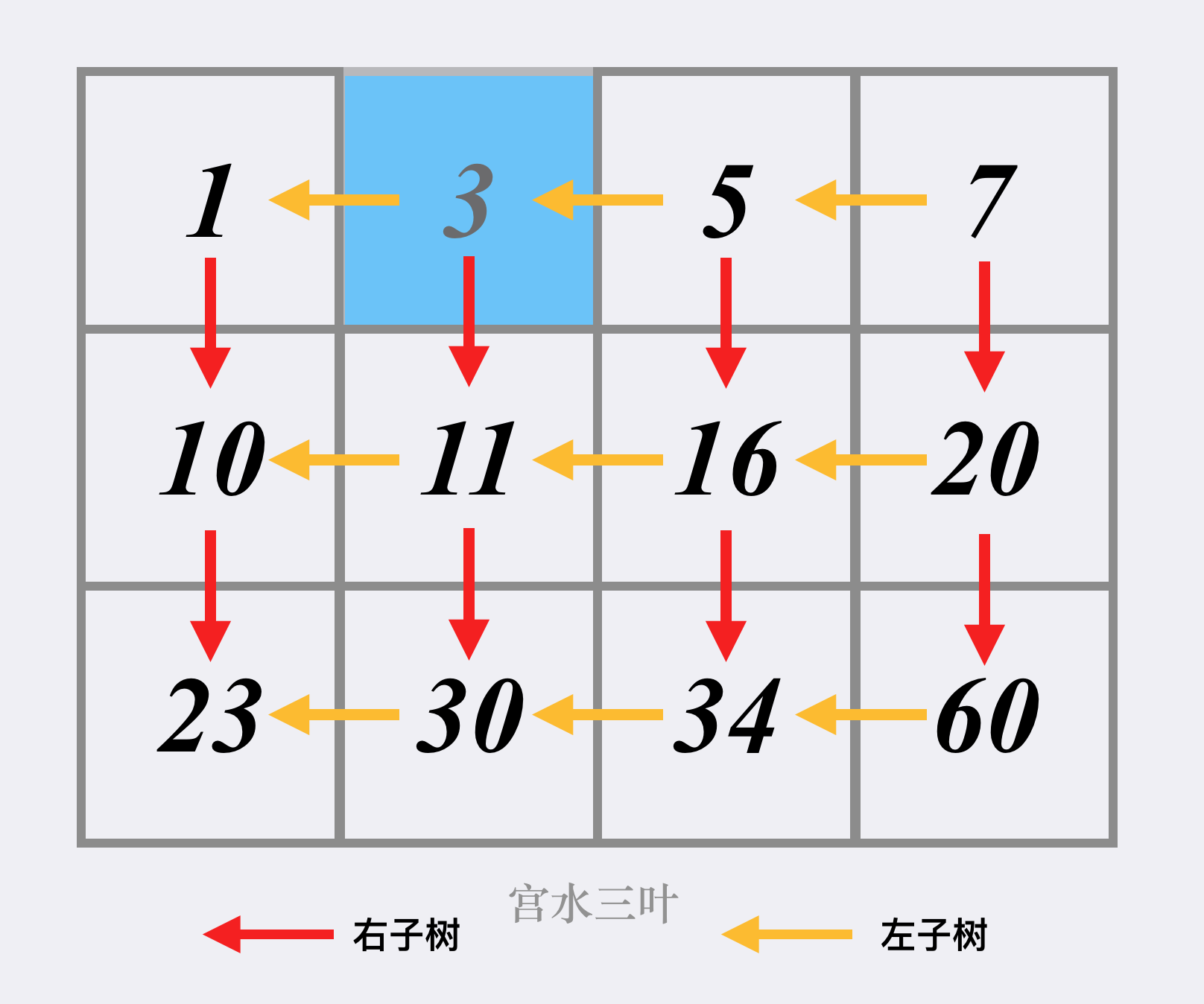
那么我们可以从根(右上角)开始搜索,如果当前的节点不等于目标值,可以按照树的搜索顺序进行:
-
当前节点「大于」目标值,搜索当前节点的「左子树」,也就是当前矩阵位置的「左方格子」,即 y-- -
当前节点「小于」目标值,搜索当前节点的「右子树」,也就是当前矩阵位置的「下方格子」,即 x++
Java 代码:
class Solution {
int m, n;
public boolean searchMatrix(int[][] mat, int t) {
m = mat.length; n = mat[0].length;
int x = 0, y = n - 1;
while (check(x, y) && mat[x][y] != t) {
if (mat[x][y] > t) y--;
else x++;
}
return check(x, y) && mat[x][y] == t;
}
boolean check(int x, int y) {
return x >= 0 && x < m && y >= 0 && y < n;
}
}
C++ 代码:
class Solution {
public:
int m, n;
bool searchMatrix(vector<vector<int>>& mat, int t) {
m = mat.size(); n = mat[0].size();
int x = 0, y = n - 1;
while (check(x, y) && mat[x][y] != t) {
if (mat[x][y] > t) y--;
else x++;
}
return check(x, y) && mat[x][y] == t;
}
bool check(int x, int y) {
return x >= 0 && x < m && y >= 0 && y < n;
}
};
Python 代码:
class Solution:
def searchMatrix(self, mat, t):
m, n = len(mat), len(mat[0])
x, y = 0, n - 1
while self.check(m, n, x, y) and mat[x][y] != t:
if mat[x][y] > t:
y -= 1
else:
x += 1
return self.check(m, n, x, y) and mat[x][y] == t
def check(self, m, n, x, y):
return 0 <= x < m and 0 <= y < n
TypeScript 代码:
function check(m: number, n: number, x: number, y: number): boolean {
return x >= 0 && x < m && y >= 0 && y < n;
}
function searchMatrix(mat: number[][], t: number): boolean {
const m = mat.length, n = mat[0].length;
let x = 0, y = n - 1;
while (check(m, n, x, y) && mat[x][y] !== t) {
if (mat[x][y] > t) y--;
else x++;
}
return check(m, n, x, y) && mat[x][y] === t;
};
-
时间复杂度: -
空间复杂度:
最后
巨划算的 LeetCode 会员优惠通道目前仍可用 ~
使用福利优惠通道 leetcode.cn/premium/?promoChannel=acoier,年度会员 有效期额外增加两个月,季度会员 有效期额外增加两周,更有超大额专属 🧧 和实物 🎁 福利每月发放。
我是宫水三叶,每天都会分享算法知识,并和大家聊聊近期的所见所闻。
欢迎关注,明天见。
更多更全更热门的「笔试/面试」相关资料可访问排版精美的 合集新基地 🎉🎉























 4万+
4万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








