Surface Normal Averaging
摘要Abstract:正确设置网格面上点的法向,对几何体在光照等情况下显示得更真实,这样就可以减少顶点数量,提高渲染速度。本文通过将OpenCascade中的形状离散成网格数据后在OpenSceneGraph中显示,及使用OSG的快速法向osgUtil::SmoothingVisitor优化与使用OpenCascade来计算正确的法向的结果的对比,说明面法向量的重要性。
关键字Key Words:OpenCascade, OpenSceneGraph, Normal Averaging, Triangulation Mesh
一、引言 Introduction
OpenGL中的顶点(Vertex)不是一个值,而由其空间坐标值、法向、颜色坐标、纹理坐标、雾坐标等所组成的一个集合。一个最基本的几何体对象至少需要设置一个合法的顶点数组,并记录顶点数据;如有必要,还可以设置颜色数组、法线数组、纹理坐标数组等多种信息。
在很多应用中,网格上的各点都需要一个表面法向量,它的作用非常广泛。例如可用来计算光照、背面剔除、模拟粒子系统在表面的“弹跳”效果、通过只需要正面而加速碰撞检测等。
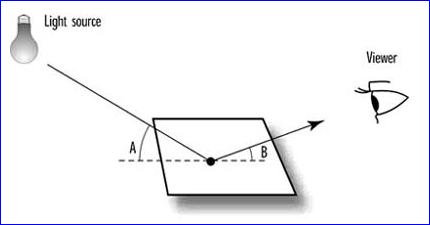
Figure 1.1 Lighting on a surface
Figure 1.2 Light is reflected off objects at specific angles
如上图所示,物体在光照情况下的反射光等的计算是与法向N有关的。
二、OpenCascade中面的法向计算 Finding Normal for OpenCascade Face
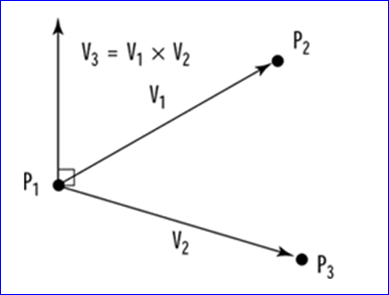
在OpenCascade中可以将拓朴形状转换成STL格式的文件进行模型的数据交换。其中STL结构中只保存了三角网格的顶点坐标和三角面的法向量。为了将拓朴数据转换成STL的网格数据,先将拓朴形状进行三角剖分,再将剖分的网格保存成STL即可。其中每个三角面的法向计算也是直接根据两个向量的叉乘得来。
Figure 2.1 A normal vector as cross product of two vectors
实现文件是RWStl.cxx,其中计算法向的程序代码如下所示:
//=====================================================================//function : WriteBinary //purpose : write a binary STL file in Little Endian format //===================================================================== Standard_Boolean RWStl::WriteBinary (const Handle(StlMesh_Mesh)& theMesh, const OSD_Path& thePath, const Handle(Message_ProgressIndicator)& theProgInd) { OSD_File aFile (thePath); aFile.Build (OSD_WriteOnly, OSD_Protection()); Standard_Real x1, y1, z1; Standard_Real x2, y2, z2; Standard_Real x3, y3, z3; // writing 80 bytes of the trash? char sval[80]; aFile.Write ((Standard_Address)sval,80); WriteInteger (aFile, theMesh->NbTriangles()); int dum=0; StlMesh_MeshExplorer aMexp (theMesh); // create progress sentry for domains Standard_Integer aNbDomains = theMesh->NbDomains(); Message_ProgressSentry aDPS (theProgInd, "Mesh domains", 0, aNbDomains, 1); for (Standard_Integer nbd = 1; nbd <= aNbDomains && aDPS.More(); nbd++, aDPS.Next()) { // create progress sentry for triangles in domain Message_ProgressSentry aTPS (theProgInd, "Triangles", 0, theMesh->NbTriangles (nbd), IND_THRESHOLD); Standard_Integer aTriangleInd = 0; for (aMexp.InitTriangle (nbd); aMexp.MoreTriangle(); aMexp.NextTriangle()) { aMexp.TriangleVertices (x1,y1,z1,x2,y2,z2,x3,y3,z3); //pgo aMexp.TriangleOrientation (x,y,z); gp_XYZ Vect12 ((x2-x1), (y2-y1), (z2-z1)); gp_XYZ Vect13 ((x3-x1), (y3-y1), (z3-z1)); gp_XYZ Vnorm = Vect12 ^ Vect13; Standard_Real Vmodul = Vnorm.Modulus (); if (Vmodul > gp::Resolution()) { Vnorm.Divide(Vmodul); } else { // si Vnorm est quasi-nul, on le charge a 0 explicitement Vnorm.SetCoord (0., 0., 0.); } WriteDouble2Float (aFile, Vnorm.X()); WriteDouble2Float (aFile, Vnorm.Y()); WriteDouble2Float (aFile, Vnorm.Z()); WriteDouble2Float (aFile, x1); WriteDouble2Float (aFile, y1); WriteDouble2Float (aFile, z1); WriteDouble2Float (aFile, x2); WriteDouble2Float (aFile, y2); WriteDouble2Float (aFile, z2); WriteDouble2Float (aFile, x3); WriteDouble2Float (aFile, y3); WriteDouble2Float (aFile, z3); aFile.Write (&dum, 2); // update progress only per 1k triangles if (++aTriangleInd % IND_THRESHOLD == 0) { if (!aTPS.More()) break; aTPS.Next(); } } } aFile.Close(); Standard_Boolean isInterrupted = !aDPS.More(); return !isInterrupted; }
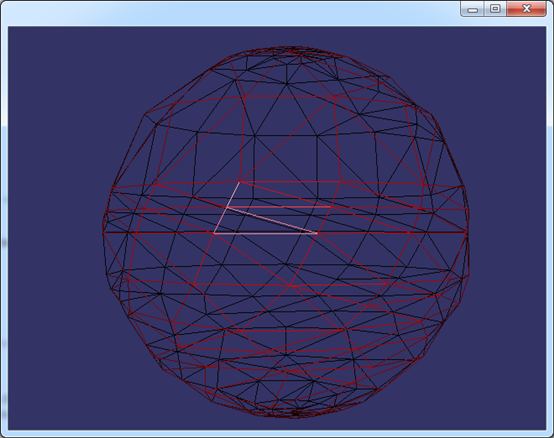
这种方式渲染的图形效果如下图所示:
Figure 2.2 A typical sphere made up of triangles
上面的球面是由三角形组成,由OpenCascade的三角剖分算法生成。如果将每个三角面的法向作为每个顶点的法向,则渲染效果如下图所示:
Figure 2.3 Specific the triangle face normal as the vertex normal of the trangle
如上图所示,在光照效果下每个三角面界限分明,感觉不是很光滑,面之间的过渡很生硬。
三、OpenSceneGraph中面的法向计算 Finding Normal for OpenSceneGraph Mesh
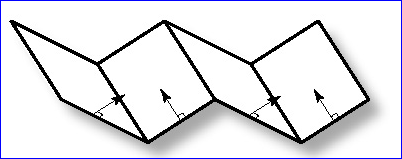
直接将网格顶点的法向设置成三角面的法向产生的效果不是很理想,通过改变顶点法向的方向可以让曲面更滑,这种技术称为法向平均(Normal Averaging)。利用法向平均技术可以产生一些有意思的视觉效果。如果有个面像下面图所示:
Figure 3.1 Jagged surface with the usual surface normals
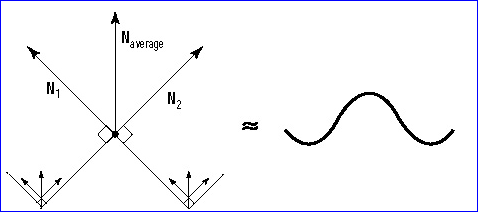
当我们考虑两个相连面的顶点处的法向为两相连面的法向的平均值时,那么这两个相连表面的连接处在OpenGL中渲染时看上去就不那么棱角分明了,如下图所示:
Figure 3.2 Averaging the normals will make sharp corners appear softer
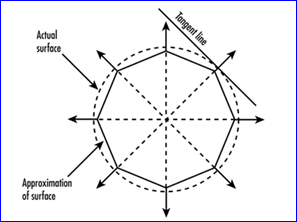
对于球面或更一般的自由曲面,法向平均的算法也是适用的。如下图所示:
Figure 3.3 An approximation with normals perpendicular to each face
Figure 3.4 Each normal is perpendicular to the surface itself
球面的法向计算还是相当简单的。但是对于一般的曲面就不是那么容易了。这种情况下需要计算多边形面片相连处的顶点的法向,将相连接处的顶点的法向设置为各相邻面的平均法向后,视觉效果还是很棒的,光滑。
The actual normal you assign to that vertex is the average of these normals. The visual effect is a nice, smooth, regular surface, even though it is actually composed of numerous small, flat segments.
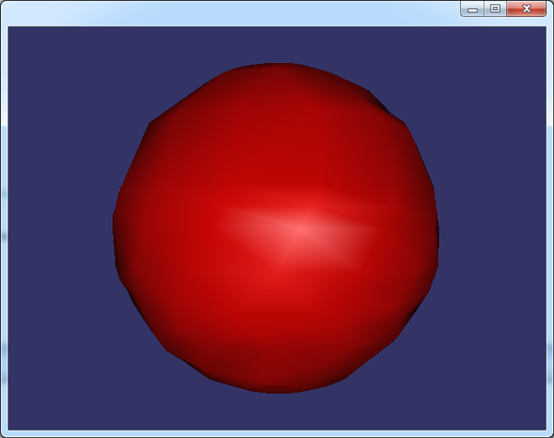
在OpenSceneGraph中生成顶点法向量的类是osgUtil::SmoothingVisitor,它使用了Visitor的模式,通过遍历场景中的几何体,生成顶点的法向量。对于上面同一个球的网格,使用osgUtil::SmoothingVisitor生成法向后在光照下的显示效果如下图所示:
Figure 3.5 Use osgUtil::SmoothingVisitor to generate normals for the sphere
四、计算正确的法向 Finding the Correct Normal for the Face
不管是STL中三角面的法向还是使用osgUtil::SmoothingVisitor来生成面的法向都是无奈之举,因为都是在离散的三角网格上找出法向,不精确,在光照下渲染效果都不是很理想。但是OpenCascade作为几何造型内核,提供了计算曲面法向的功能,因此有能力计算出顶点处的法向的精确值。
当计算网格曲面顶点的法向时,共享顶点处的法向最好设置为顶点各相连面的法向的平均值。对于参数化的曲面,是可以直接计算出每个顶点处的法向,就不需要再求法向平均值了,因为已经有了曲面法向数学定义的值。所以在OpenCascade中计算出来曲面中某个顶点的法向就是数学定义上面的法向。计算方法如下:
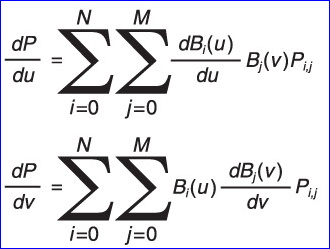
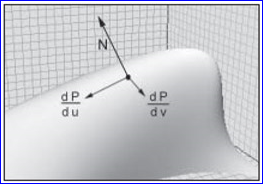
对顶点处的参数u,v分别求一阶导数,得出顶点处在u,v方向的切向量,如下图所示:
Figure 4.1 Derivatives with respect to u and v
Figure 4.1 Tangents on a surface
将u和v方向的切向量叉乘就得到了该顶点处的法向,计算方法如下所示:
叉乘后顶点处的法向如下图所示:
Figure 4.2 Normal on a surface
OpenCascade中计算曲面表面属性的类是BRepLProp_SLProps,计算法向部分程序如下所示:
Standard_Boolean LProp_SLProps::IsNormalDefined() { if (normalStatus == LProp_Undefined) { return Standard_False; } else if (normalStatus >= LProp_Defined) { return Standard_True; } // first try the standard computation of the normal. CSLib_DerivativeStatus Status; CSLib::Normal(d1U, d1V, linTol, Status, normal); if (Status == CSLib_Done ) { normalStatus = LProp_Computed; return Standard_True; } normalStatus = LProp_Undefined; return Standard_False; }
此类的使用方法如下所示:
const TopoDS_Face& theFace = TopoDS::Face(faceExp.Current()); BRepLProp_SLProps theProp(BRepAdaptor_Surface(theFace), 1, Precision::Confusion()); theProp.SetParameters(u, v); if (theProp.IsNormalDefined()) { gp_Vec theNormal = theProp.Normal(); }
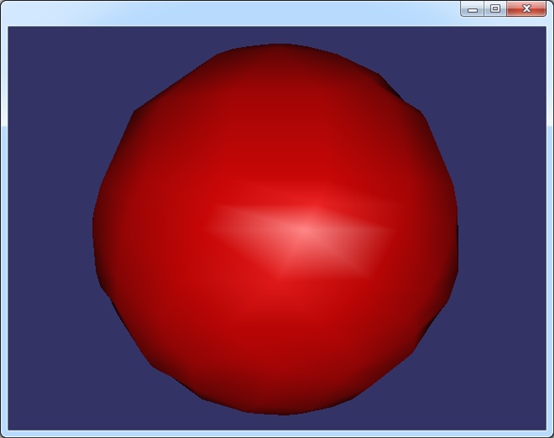
计算法向后渲染效果如下图所示:
Figure 4.3 Sphere vertex normals computed by BRepLProp_SLProps
由图可知,OpenCascade计算的面的法向在渲染时效果很好。
五、程序示例 Putting It All Together
将这三种情况产生的渲染效果放在一起来比较,程序代码如下所示:
/* * Copyright (c) 2014 eryar All Rights Reserved. * * File : Main.cpp * Author : eryar@163.com * Date : 2014-02-25 17:00 * Version : 1.0v * * Description : Learn the Normal Averaging from OpenGL SuperBible. * * Key Words : OpenCascade, OpenSceneGraph, Normal Averaging * */ // OpenCascade library. #define WNT #include <Poly_Triangulation.hxx> #include <TColgp_Array1OfPnt2d.hxx> #include <TopoDS.hxx> #include <TopoDS_Face.hxx> #include <TopoDS_Shape.hxx> #include <TopExp_Explorer.hxx> #include <BRep_Tool.hxx> #include <BRepAdaptor_Surface.hxx> #include <BRepLProp_SLProps.hxx> #include <BRepMesh.hxx> #include <BRepPrimAPI_MakeBox.hxx> #include <BRepPrimAPI_MakeCone.hxx> #include <BRepPrimAPI_MakeSphere.hxx> #pragma comment(lib, "TKernel.lib") #pragma comment(lib, "TKMath.lib") #pragma comment(lib, "TKG3d.lib") #pragma comment(lib, "TKBRep.lib") #pragma comment(lib, "TKMesh.lib") #pragma comment(lib, "TKPrim.lib") #pragma comment(lib, "TKTopAlgo.lib") // OpenSceneGraph library. #include <osg/MatrixTransform> #include <osg/Material> #include <osgGA/StateSetManipulator> #include <osgViewer/Viewer> #include <osgViewer/ViewerEventHandlers> #include <osgUtil/SmoothingVisitor> #pragma comment(lib, "osgd.lib") #pragma comment(lib, "osgDBd.lib") #pragma comment(lib, "osgGAd.lib") #pragma comment(lib, "osgUtild.lib") #pragma comment(lib, "osgViewerd.lib") #pragma comment(lib, "osgManipulatord.lib") /** * @breif Build the mesh for the OpenCascade TopoDS_Shape. * @param [in] TopoDS_Shape theShape OpenCascade TopoDS_Shape. * @param [in] Standard_Boolean bSetNormal If set to true, will set the vertex normal correctly * else will set vertex normal by its triangle face normal. */ osg::Geode* BuildMesh(const TopoDS_Shape& theShape, Standard_Boolean bSetNormal = Standard_False) { Standard_Real theDeflection = 0.1; BRepMesh::Mesh(theShape, theDeflection); osg::ref_ptr<osg::Geode> theGeode = new osg::Geode(); for (TopExp_Explorer faceExp(theShape, TopAbs_FACE); faceExp.More(); faceExp.Next()) { TopLoc_Location theLocation; const TopoDS_Face& theFace = TopoDS::Face(faceExp.Current()); const Handle_Poly_Triangulation& theTriangulation = BRep_Tool::Triangulation(theFace, theLocation); BRepLProp_SLProps theProp(BRepAdaptor_Surface(theFace), 1, Precision::Confusion()); if (theTriangulation.IsNull()) { continue; } osg::ref_ptr<osg::Geometry> theMesh = new osg::Geometry(); osg::ref_ptr<osg::Vec3Array> theVertices = new osg::Vec3Array(); osg::ref_ptr<osg::Vec3Array> theNormals = new osg::Vec3Array(); for (Standard_Integer t = 1; t <= theTriangulation->NbTriangles(); ++t) { const Poly_Triangle& theTriangle = theTriangulation->Triangles().Value(t); gp_Pnt theVertex1 = theTriangulation->Nodes().Value(theTriangle(1)); gp_Pnt theVertex2 = theTriangulation->Nodes().Value(theTriangle(2)); gp_Pnt theVertex3 = theTriangulation->Nodes().Value(theTriangle(3)); gp_Pnt2d theUV1 = theTriangulation->UVNodes().Value(theTriangle(1)); gp_Pnt2d theUV2 = theTriangulation->UVNodes().Value(theTriangle(2)); gp_Pnt2d theUV3 = theTriangulation->UVNodes().Value(theTriangle(3)); theVertex1.Transform(theLocation.Transformation()); theVertex2.Transform(theLocation.Transformation()); theVertex3.Transform(theLocation.Transformation()); // find the normal for the triangle mesh. gp_Vec V12(theVertex1, theVertex2); gp_Vec V13(theVertex1, theVertex3); gp_Vec theNormal = V12 ^ V13; gp_Vec theNormal1 = theNormal; gp_Vec theNormal2 = theNormal; gp_Vec theNormal3 = theNormal; if (theNormal.Magnitude() > Precision::Confusion()) { theNormal.Normalize(); theNormal1.Normalize(); theNormal2.Normalize(); theNormal3.Normalize(); } theProp.SetParameters(theUV1.X(), theUV1.Y()); if (theProp.IsNormalDefined()) { theNormal1 = theProp.Normal(); } theProp.SetParameters(theUV2.X(), theUV2.Y()); if (theProp.IsNormalDefined()) { theNormal2 = theProp.Normal(); } theProp.SetParameters(theUV3.X(), theUV3.Y()); if (theProp.IsNormalDefined()) { theNormal3 = theProp.Normal(); } if (theFace.Orientation() == TopAbs_REVERSED) { theNormal.Reverse(); theNormal1.Reverse(); theNormal2.Reverse(); theNormal3.Reverse(); } theVertices->push_back(osg::Vec3(theVertex1.X(), theVertex1.Y(), theVertex1.Z())); theVertices->push_back(osg::Vec3(theVertex2.X(), theVertex2.Y(), theVertex2.Z())); theVertices->push_back(osg::Vec3(theVertex3.X(), theVertex3.Y(), theVertex3.Z())); if (bSetNormal) { theNormals->push_back(osg::Vec3(theNormal1.X(), theNormal1.Y(), theNormal1.Z())); theNormals->push_back(osg::Vec3(theNormal2.X(), theNormal2.Y(), theNormal2.Z())); theNormals->push_back(osg::Vec3(theNormal3.X(), theNormal3.Y(), theNormal3.Z())); } else { theNormals->push_back(osg::Vec3(theNormal.X(), theNormal.Y(), theNormal.Z())); theNormals->push_back(osg::Vec3(theNormal.X(), theNormal.Y(), theNormal.Z())); theNormals->push_back(osg::Vec3(theNormal.X(), theNormal.Y(), theNormal.Z())); } } theMesh->setVertexArray(theVertices); theMesh->setNormalArray(theNormals); theMesh->setNormalBinding(osg::Geometry::BIND_PER_VERTEX); theMesh->addPrimitiveSet(new osg::DrawArrays(osg::PrimitiveSet::TRIANGLES, 0, theVertices->size())); theGeode->addDrawable(theMesh); } // Set material for the mesh. osg::ref_ptr<osg::StateSet> theStateSet = theGeode->getOrCreateStateSet(); osg::ref_ptr<osg::Material> theMaterial = new osg::Material(); theMaterial->setDiffuse(osg::Material::FRONT, osg::Vec4(1.0f, 0.0f, 0.0f, 1.0f)); theMaterial->setSpecular(osg::Material::FRONT, osg::Vec4(1.0f, 1.0f, 1.0f, 1.0f)); theMaterial->setShininess(osg::Material::FRONT, 100.0f); theStateSet->setAttribute(theMaterial); return theGeode.release(); } osg::Node* BuildScene(void) { osg::ref_ptr<osg::Group> theRoot = new osg::Group(); // 1. Build a sphere without setting vertex normal correctly. TopoDS_Shape theSphere = BRepPrimAPI_MakeSphere(1.6); osg::ref_ptr<osg::Node> theSphereNode = BuildMesh(theSphere); theRoot->addChild(theSphereNode); // 2. Build a sphere without setting vertex normal correctly, but will // use osgUtil::SmoothingVisitor to find the average normals. osg::ref_ptr<osg::MatrixTransform> theSmoothSphere = new osg::MatrixTransform(); osg::ref_ptr<osg::Geode> theSphereGeode = BuildMesh(theSphere); theSmoothSphere->setMatrix(osg::Matrix::translate(5.0, 0.0, 0.0)); // Use SmoothingVisitor to find the vertex average normals. osgUtil::SmoothingVisitor sv; sv.apply(*theSphereGeode); theSmoothSphere->addChild(theSphereGeode); theRoot->addChild(theSmoothSphere); // 3. Build a sphere with setting vertex normal correctly. osg::ref_ptr<osg::MatrixTransform> theBetterSphere = new osg::MatrixTransform(); osg::ref_ptr<osg::Geode> theSphereGeode1 = BuildMesh(theSphere, Standard_True); theBetterSphere->setMatrix(osg::Matrix::translate(10.0, 0.0, 0.0)); theBetterSphere->addChild(theSphereGeode1); theRoot->addChild(theBetterSphere); return theRoot.release(); } int main(int argc, char* argv[]) { osgViewer::Viewer viewer; viewer.setSceneData(BuildScene()); viewer.addEventHandler(new osgViewer::StatsHandler()); viewer.addEventHandler(new osgViewer::WindowSizeHandler()); viewer.addEventHandler(new osgGA::StateSetManipulator(viewer.getCamera()->getOrCreateStateSet())); return viewer.run(); }
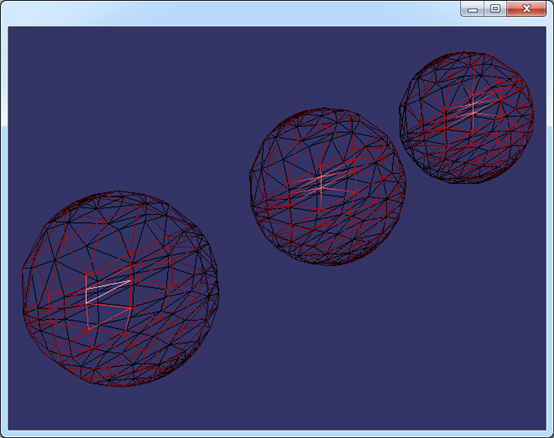
生成效果图如下所示:
Figure 5.1 Same sphere triangulation mesh
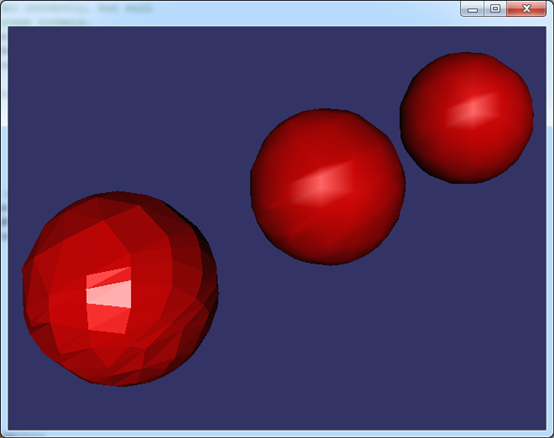
Figure 5.2 Same sphere mesh with different vertex normals
由上图可知,相同的球面网格,当顶点的法向为三角面的法向时,在有光照的情况下,渲染效果最差。使用osgUtil::SmoothingVisitor法向生成算法生成的顶点法向与使用类BRepLProp_SLProps计算出的法向,在光照情况下显示效果相当。
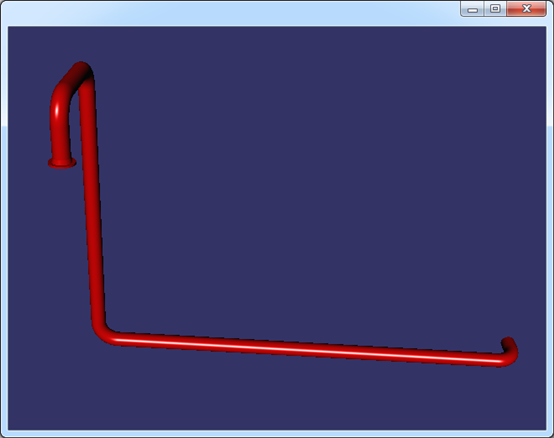
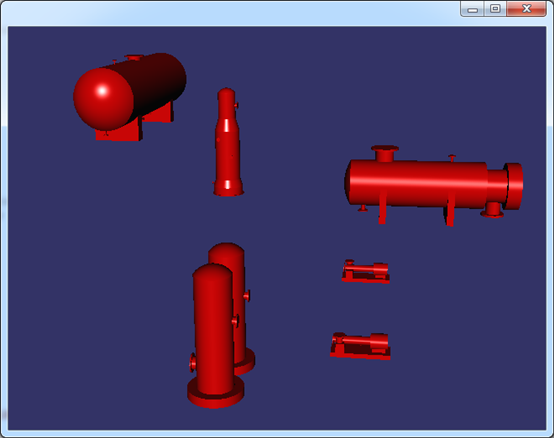
Figure 5.3 Pipe and equipments with correct vertex normals
六、结论 Conclusion
正确设置网格面顶点的法向可以在光照环境中看上去更光滑真实。利用法向平均算法或使用曲面的参数方程求解曲面顶点上法向,可以在满足显示效果基本相同的条件下减少网格顶点的数量,可以提高渲染速度。
七、参考资料 References
1. Waite group Press, OpenGL Super Bible(1st), Macmillan Computer Publishing, 1996
2. Richard S. Wright Jr., Benjamin Lipchak, OpenGL SuperBible(3rd), Sams Publishing, 2004
3. vsocc.cpp in netgen
4. Kelly Dempski, Focus on Curves and Surfaces, Premier Press, 2003
5. 王锐,钱学雷,OpenSceneGraph三维渲染引擎设计与实践,清华大学出版社
6. 肖鹏,刘更代,徐明亮,OpenSceneGraph三维渲染引擎编程指南,清华大学出版社
PDF Version: Surface Normal Averaging




























 605
605

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








