收敛区间 收敛域_函数族的一致收敛及其性质

此两者，同出而异名，同谓之玄。 ----老子《道德经》

高数学到了函数项级数和含参积分这一块，觉得教科书把本来统一优美的过程处理得杂乱而不清晰，有种只见树木不见森林的感觉。故以大家喜闻乐见的“一致收敛”为线索，写下此文以做总结和复习。内容上主要参考了卓里奇第二卷^[1]，并加上了一些我自己的粗浅思考。本人并非数学专业，数学水平也十分有限，如有错漏敬望海涵。（题图为Bernstein多项式一致收敛于

)

一致收敛的定义

首先从我们熟悉的函数列

和

语言开始：

定义：对于定义在

上的函数列

，我们定义 (逐点)收敛和一致收敛如下：

注意到量词位置的不同导致了两个定义的区别：前者的

依赖于

，而后者则没有。

命题：

证明：由定义可直接验证。
Remark: 如果对

上的函数空间引入Chebyshev度量

,那么

等价于

作为一个整体在Chebyshev度量下收敛于

。这也是所谓“一致”(uniform)的来源。回忆一致连续的概念，是不是有这种感觉？

^[2]从几何直观的角度来说，给定一个曲线簇和目标曲线，对任意

，总能找到曲线簇中的一条，它以及它的所有后继曲线与目标曲线之间的“竖直方向误差上限”小于

。逐点收敛则没有这样直观自然的整体和几何意义，从泛函分析的角度看是不够"好"的。

我们再来看同样熟悉的含参瑕积分

(以a为瑕点)和

语言:

定义：对于定义在

上的含参积分

，我们定义对应的瑕积分的(逐点)收敛和一致收敛如下：

很难不注意到此定义与函数列之间的相似性。事实上，我们先前对函数列的Remark对含参瑕积分完全成立，只用将离散极限过程

改为连续极限过程

即可。

我们还可以如法炮制地写出函数项级数和含参广义积分的(逐点)收敛以及一致收敛的定义，其结果大同小异，其核心都在于参数的极限过程是否依赖于自变量的选择。这种结构上的惊人相似启示着其背后很可能存在更加普适的深层结构，我们刚刚研究的含参积分和函数列只是其导出的特例而已。

普适的代价是抽象。为了统一各种极限过程，并严谨叙述之前得到的定性发现，我们将使用滤子基(filter base)来对其进行描述。由于篇幅所限，在此不对其进行详细介绍。简而言之，滤子基抓住了极限过程的拓扑本质，并可以描述包括求导,Riemann积分在内的各种建立在极限上的微积分算子，同时把极限从

等较好空间推广到了任何定义了相应滤子基的拓扑空间。感兴趣的读者可以参看卓里奇第一卷第三章的相关部分以及这篇介绍

^[3]：

那么坐好，我们加速了：

定义：设

是度量空间，称二元函数

为

依赖于参数t的函数族,记为

Remark: 1.开始举的两个例子中，参数域

分别为

，由此可见函数列和含参广义积分都是依赖于参数的函数族 。2.这里甚至不要求

是完备的，不过

不完备时一致收敛的Cauchy准则不再成立。3.参数域和定义域是对偶的，选取哪个作为参数域都可以。

定义：设

为

的一个滤子基，

在

上关于

(逐点)收敛和一致收敛定义为：

Remark: 同样地，我们可以引入Chebyshev度量

，一致收敛仍然等价于

该度量下关于

收敛至

。

定理(Cauchy准则)：设

为依赖于参数

的函数族，

为

的一个滤子基，

是完备度量空间，那么在

上：

证明: 必要性： 由一致收敛的定义显然。充分性：给定

,

作为

的函数满足单元函数对

的Cauchy准则。即

。

,在表达式

中取

,得

，

由此可推出

成立。

Remark: 注意到在函数极限的Cauchy准则充分性的证明中也用到了在不等式中取极限这一操作，并将问题继续转化为Cauchy列是否是收敛的充分条件。对

完备性的要求便来自这一步。

一致收敛函数族的性质

我们刚刚研究了参数域上的极限过程

。一个问题是我们所关心的：如果函数族中的每个函数都携带着自身定义域上的极限过程

，它们之间是否可交换？下面介绍函数族的核心定理，它提供了这两个极限过程可交换的判定条件。（物理系狂喜）

定理: （极限交换基本原理）^[4]设

为度量空间，

为依赖于参数

的函数族，

,

为

,

的滤子基。如果 :

那么

关于

的两个累次极限存在，且有：

举一个大家更加熟悉的例子予以说明：若定义在

上的函数项级数在

上满足

那么有：

和

呈现出了一种对偶关系。如果我们视

为参数，将收敛变成

关于

一致

的：

此定理告诉我们

式仍然成立。

下面给出定理的证明：

证明：由

，

，由Cauchy准则的必要性不难得出：

由于

，固定

，有

，使得:

分别在

和

式中对

在

和

上取极限得：

由以上三个不等式，有：

得证。

Remark：如果

作为度量空间是完备的，那么条件

是不需要的。对

式关于

取极限，结合Cauchy准则即可得到

和

式。

有趣的是，这个定理还可以表示为一个diagram：黑线表示条件，蓝线表示结论。这个图是可交换的，也就是说从左上角到右下角的结果不依赖于取极限的具体顺序。^[5]

LaTeX新手实在是搞不出交换图，遂手绘之

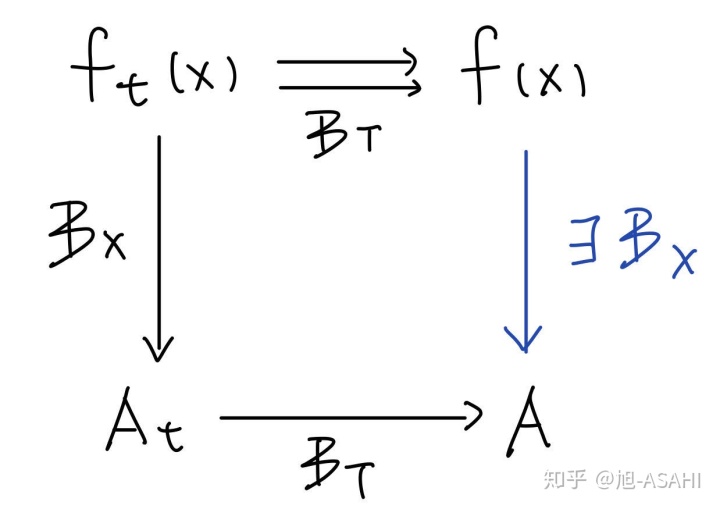
下面我们将用极限交换基本原理来导出函数族的一些重要性质。

定理：(连续性与极限过渡) 设

为度量空间，

为依赖于参数

的函数族，

为

的滤子基。如果

，且每个函数

在

连续，那么

在

处也连续。

证明：令

为过程

,对照极限交换基本原理得证。

定理：(积分法与极限过渡)^[6]设

为依赖于参数

的函数族，

是一个完备的赋范线性空间，

,

为

的滤子基，在

上有

，那么：

证明: 令

为

上所有带标志点分划的集合，考虑

,

的Riemann和

因为

，

,

时：

因此在

上有

。在

中取我们熟悉的滤子基

:

, Riemann和

在此基下的极限便是Riemann积分

。对照极限交换基本原理，交换图上的蓝线便是定理的结论。

定理：(微分法与极限过渡) 设

是一个线性赋范空间中的有界凸子集，

是一个完备的线性赋范空间。

为依赖于参数

的函数族，

是

中的基。如果

在

上可微，

,且

。那么

证明： 由有限增量定理，

由

和

可知：

由函数族一致收敛的Cauchy准则，这证明了

。再做以下估计：

对于固定的

，定义

以及函数族

由

,

易知：

注意到

是由

的可微性诱导出来的，在

中存在我们于微分学中熟悉的滤子基

,自然地，有

和

成立。对照极限交换基本原理，交换图上的蓝线便证明了

的可微性以及

。

总结：

一致收敛是一个很奇妙的概念。内涵上，它蕴含了某种整体性质；外延上，它出现在函数列，函数项级数以及含参广义积分等看似不相关联的对象之中。本文从这个角度出发，进行了两层抽象。第一层抽象将用含参函数族这一概念统一了这些不同对象，极大地方便了后续的讨论；第二层抽象则抛弃了传统的实数域，通过滤子基，度量等语言尽量减少内涵，从而最大程度地增加外延，最终将一致收敛的概念拓展至更加抽象的空间中。文章的后半部分在保留了这种抽象性的基础上证明了一致收敛的结构性定理：极限交换基本原理，(还发现了一张好看的交换图)。最后用三个传统换序问题的抽象空间版本展示了极限交换基本定理的强大威力，在较为现代的语言描述下^[7]，我们能够更清晰地看到古典分析学的本质。

参考

1. ^《数学分析（第二卷）》B.A.卓里奇著
2. ^事实上，一致连续和一致收敛之间是有联系的。参考常义瑕积分的相关定理的证明就可以发现这一点。
3. ^https://zhuanlan.zhihu.com/p/112680689
4. ^这个名字是在谢惠民上看到的。
5. ^由于我对范畴论等知识实在不甚了解，不清楚其背后有无更加深刻的意义。
6. ^本定理及证明中延续卓里奇第一卷第六章中的记号。
7. ^不足之处是没有对它们进行很好的介绍，我下次会注意这一点的。