四元数左乘右乘_使用OpenCV的四元数

作者：单晨琪 孔良潜 王龙步（华为开源能力中心）

在新发布的OpenCV 4.5.1中，我们为OpenCV贡献了四元数的功能。本文对此功能进行介绍。

四元数简介

四元数由爱尔兰数学家W.R.Hamilton在1843年提出并建立相关理论。它可以表示三维空间的旋转。

四元数可以通过如下五种方式进行定义：

四元数的创建：

1.通过旋转轴和旋转角创建四元数

轴角的含义是绕某个轴旋转一定角度，围绕单位旋转轴u以旋转角θ进行旋转的四元数：

using namespace cv; 
double angle = CV_PI; 
Vec3d axis = {0, 0, 1}; //旋转轴不需要用户单独执行归一化操作
Quatd q = Quatd::createFromAngleAxis(angle, axis);

2.通过四个实数w, x, y, z创建四元数

Quatd q(1, 2, 3, 4);

3.使用4维Vector创建四元数

Vec4d vec{1, 2, 3, 4}; 
Quatd q(vec); //[1,2,3,4]
Vec4f vec{1, 2, 3, 4}; 
Quatf q(vec); //[1,2,3,4]

4 . 通过旋转矩阵R创建四元数

Quatd q = Quatd::createFromRotMat(R)

四元数的计算

在这里的函数基本上都可以通过func(obj)的形式进行操作，例如exp(q)，而无需写成不容易阅读的形式q.exp()。当你确定在操作中的四元数是一个归一化的四元数时，可以通过添加枚举类QuatAssumeType中的QUAT_ASSUME_UNIT参数来加速运算，当然不加也不会有影响。

1.四元数取值：

共有三种方式获取四元数的实数部分：

Quatf q(1,2,3,4); 
std::cout << q.w << std::endl; // w=1, x=2, y=3, z=4 
std::cout << q[0] << std::endl; // q[0]=1, q[1]=2, q[2]=3, q[3]=4 
std::cout << q.at(0) << std::endl;// 1

2.叉乘 crossProduct

Quatd q{1,2,3,4}; 
Quatd p{5,6,7,8}; 
p.crossProduct(q);//Quat [0,-4,8,-4]

3.点乘 dot

Quatd q(1,2,3,4); 
Quatd p(5,6,7,8); 
p.dot(q);//70

4.指数计算

四元数指数计算公式：

Quatd q{1,2,3,4}; 
cout << q.exp() << endl;//Quat [1.69392, -0.78956, -1.184634, -1.57912]

//or
exp(q);

5.计算旋转角

Quatd q(1,2,3,4); 
q.getAngle(); //2.77438
QuatAssumeType assumeUnit = QUAT_ASSUME_UNIT; 
q.normalize().getAngle(assumeUnit);//与q.getAngle()相同。用户也可以先将四元数进行归一化，再求旋转角

6.计算旋转轴：

Quatd q(1,2,3,4); 
q.getAxis(); //[0.371391, 0.557086, 0.742781]
QuatAssumeType assumeUnit = QUAT_ASSUME_UNIT; 
q.normalize().getAxis(assumeUnit);//same as q.getAxis()

7.求逆运算

Quatd q(1,2,3,4); 
q.inv(); //Quat [0.0333333, -0.0666667, -0.1, -0.133333]
QuatAssumeType assumeUnit = QUAT_ASSUME_UNIT;
q = q.normalize(); 
q.inv(assumeUnit); //Quat [0.182574, -0.365148, -0.547723, -0.730297]
                   //参数assumeUnit 表示 p 是已经归一化的四元数

8.求sin, cos值

Quatd q(1,2,3,4); 
q.sin(); //Quat [91.7837, 21.8865, 32.8297, 43.773]
//or
sin(q);
q.cos(); //Quat [58.9336, -34.0862, -51.1293, -68.1724]
//or
cos(q);

9.其他部分运算

本文列出四元数的常用基本运算，更多详情可见https://docs.opencv.org/master/da/d4a/classcv_1_1Quat.html

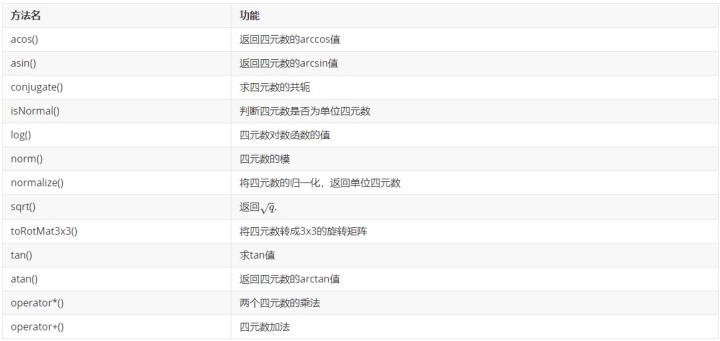
四元数的应用

利用四元数，将坐标上的点进行旋转：

对于坐标上的点 , 根据四元数q进行旋转，得到新的坐标

double angle = CV_PI;
Vec3d axis{0,0,1};
Quatd q_unit = Quatd::createFromAngleAxis(angle, axis);
//假设旋转点(1,0,1)
Mat pointsA = (Mat_<double>(1, 3) << 1,0,1);
//change the shape
pointsA = pointsA.t();
// 将两个点围绕z轴旋转180度
// 1.通过将四元数转换为旋转矩阵后，再求解新的坐标
Mat new_point1 = q_unit.toRotMat3x3() * pointsA;
// 打印结果
cout << new_point1 << endl; //[-1; 1.224646799147353e-16; 1]
//2. 将坐标转化为四元数，在通过四元数的乘法求解新的坐标
Mat new_point2 =  q_unit * pointsA * (q_unit.inv());
cout << new_point2 << endl; //Quat [0, -1, 1.22465e-16, 1]

参考文献：http://en.wikipedia.org/wiki/Quaternion

OpenCV中国团队于2019年9月由深圳市人工智能与机器人研究院支持成立，非营利目的，致力于OpenCV的开发、维护和推广工作。

长按下方QR码关注我们获取最新动态