【控制】《复杂运动体系统的分布式协同控制与优化》-方浩老师-第2章-基于速度估计的多欧拉-拉格朗日系统分布式控制-CSDN博客

本文链接：https://blog.csdn.net/weixin_36815313/article/details/112344828

第1章	回到目录	第3章

第2章-基于速度估计的多欧拉-拉格朗日系统分布式控制

2.1 引言

2.2 模型与问题描述

2.2.1 欧拉-拉格朗日系统

2.2.2 问题描述

2.3 动态领航者状态估计器设计

滑模估计器

滑模估计器

2.5 仿真验证

设计估计器，利用公式（2.5a、2.5b、2.5c）进行领航者状态估计

% 函数

clear

% 领航者状态：Q0
% 领航者速度：V0
% 领航者加速度：A0
% 跟随者估计位置：P_EsX、P_EsY


Q0 = [0 0]';
V0 = [0 0]';
A0 = [0 0]';

P_EsX_t0 = [pi/7*1, pi/7*2, pi/7*3, pi/7*4];
P_EsY_t0 = [pi/8*1, pi/8*2, pi/8*3, pi/8*4];

V_EsX_t0 = [0, 0, 0, 0];
V_EsY_t0 = [0, 0, 0, 0];

A_EsX_t0 = [0, 0, 0, 0];
A_EsY_t0 = [0, 0, 0, 0];

% 时间参数
tBegin = 0;
tEnd   = 10;
dT     = 0.1;

% 关系参数
alpha1 = 1.5;
alpha2 = 1.5;
alpha3 = 1.5;
% 跟随者之间关系矩阵
L = [0  0  0  0;
    -1  1  0  0;
     0 -1  1  0;
     0  0 -1  1;];
% 与领航者关系矩阵
B = [1;
     0;
     0;
     0;];

[TP, P_EsX] = ode45(@(t,P_EsX) -alpha1 .* sign( L*P_EsX + B.*(P_EsX-( sin(t))) ), [tBegin,tEnd], P_EsX_t0);
[TPY,P_EsY] = ode45(@(t,P_EsY) -alpha1 .* sign( L*P_EsY + B.*(P_EsY-(-sin(t))) ), [tBegin,tEnd], P_EsY_t0);
P_EsX(:,5) =  sin(TP);
P_EsY(:,5) = -sin(TPY);

[TV, V_EsX] = ode45(@(t,V_EsX) -alpha2 .* sign( L*V_EsX + B.*(V_EsX-( cos(t))) ), [tBegin,tEnd], V_EsX_t0);
[TVY,V_EsY] = ode45(@(t,V_EsY) -alpha2 .* sign( L*V_EsY + B.*(V_EsY-(-cos(t))) ), [tBegin,tEnd], V_EsY_t0);
V_EsX(:,5) =  cos(TV);
V_EsY(:,5) = -cos(TVY);

[TA, A_EsX] = ode45(@(t,A_EsX) -alpha3 .* sign( L*A_EsX + B.*(A_EsX-(-sin(t))) ), [tBegin,tEnd], A_EsX_t0);
[TAY,A_EsY] = ode45(@(t,A_EsY) -alpha3 .* sign( L*A_EsY + B.*(A_EsY-( sin(t))) ), [tBegin,tEnd], A_EsY_t0);
A_EsX(:,5) = -sin(TA);
A_EsY(:,5) =  sin(TAY);

% 绘制结果图
figure(1)

subplot(2,1,1)
plot(TP,P_EsX(:,1), TP,P_EsX(:,2), TP,P_EsX(:,3), TP,P_EsX(:,4), TP,P_EsX(:,5),'linewidth',1.5 ); 
legend('运动体1','运动体2', '运动体3','运动体4', '运动体0'); title('机械臂位置估计'); 
xlabel('t/s'); ylabel('q_{i(1)}/rad');
grid on

subplot(2,1,2)
plot(TPY,P_EsY(:,1),TPY,P_EsY(:,2),TPY,P_EsY(:,3),TPY,P_EsY(:,4),TPY,P_EsY(:,5),'linewidth',1.5 ); 
legend('运动体1','运动体2', '运动体3','运动体4', '运动体0'); title('机械臂位置估计'); 
xlabel('t/s'); ylabel('q_{i(2)}/rad');
grid on

figure(2)

subplot(2,1,1)
plot(TV,V_EsX(:,1), TV,V_EsX(:,2), TV,V_EsX(:,3), TV,V_EsX(:,4), TV,V_EsX(:,5),'linewidth',1.5 ); 
legend('运动体1','运动体2', '运动体3','运动体4', '运动体0'); title('机械臂速度估计'); 
xlabel('t/s'); ylabel('q_{i(1)}/rad');
grid on

subplot(2,1,2)
plot(TVY,V_EsY(:,1),TVY,V_EsY(:,2),TVY,V_EsY(:,3),TVY,V_EsY(:,4),TVY,V_EsY(:,5),'linewidth',1.5 ); 
legend('运动体1','运动体2', '运动体3','运动体4', '运动体0'); title('机械臂速度估计'); 
xlabel('t/s'); ylabel('q_{i(2)}/rad');
grid on

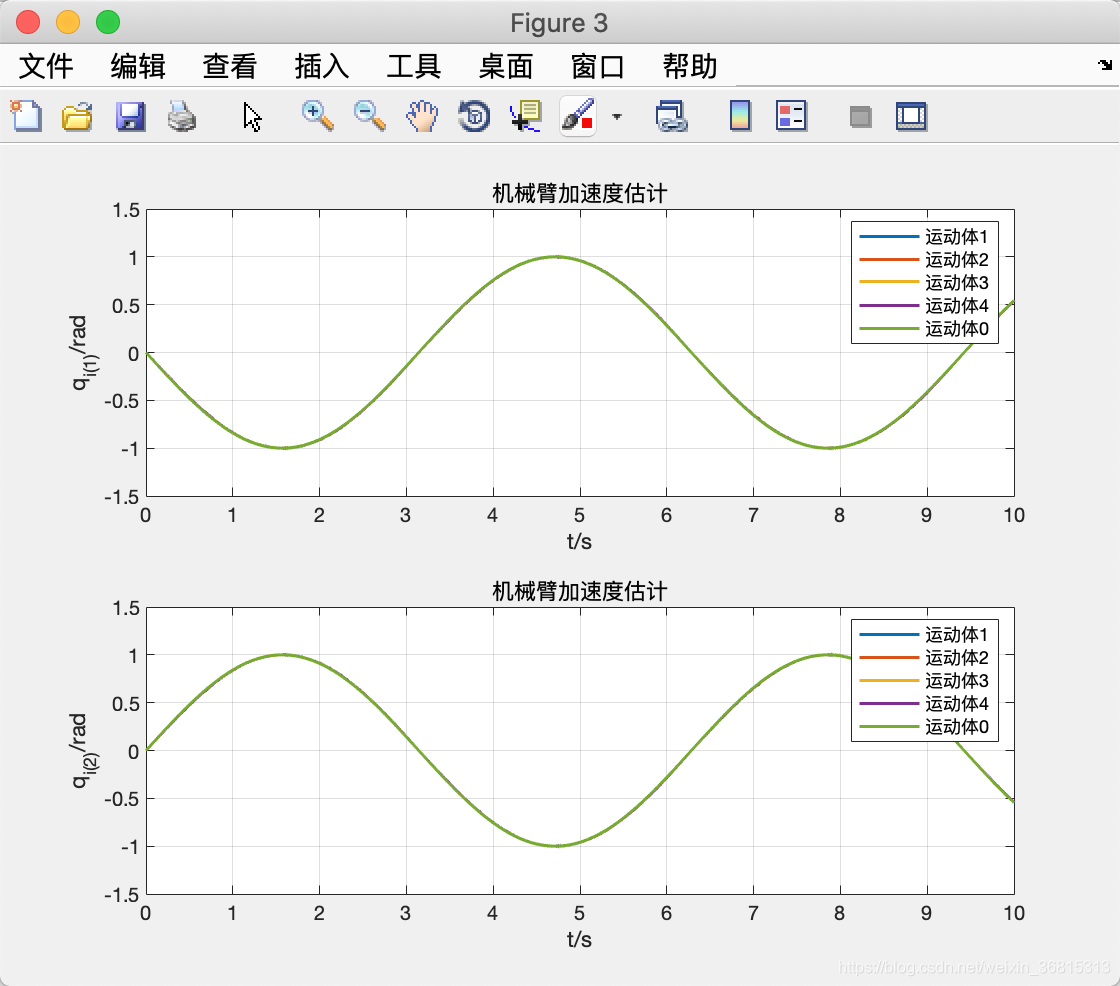
figure(3)

subplot(2,1,1)
plot(TA,A_EsX(:,1), TA,A_EsX(:,2), TA,A_EsX(:,3), TA,A_EsX(:,4), TA,A_EsX(:,5),'linewidth',1.5 ); 
legend('运动体1','运动体2', '运动体3','运动体4', '运动体0'); title('机械臂加速度估计'); 
xlabel('t/s'); ylabel('q_{i(1)}/rad');
grid on

subplot(2,1,2)
plot(TAY,A_EsY(:,1),TAY,A_EsY(:,2),TAY,A_EsY(:,3),TAY,A_EsY(:,4),TAY,A_EsY(:,5),'linewidth',1.5 ); 
legend('运动体1','运动体2', '运动体3','运动体4', '运动体0'); title('机械臂加速度估计'); 
xlabel('t/s'); ylabel('q_{i(2)}/rad');
grid on

在这里插入图片描述