【Matlab】dde23解时滞时延微分方程

最新推荐文章于 2024-04-05 12:00:00 发布

原创最新推荐文章于 2024-04-05 12:00:00 发布 · 5.3k 阅读

52 ·

CC 4.0 BY-SA版权

Simulink/Matlab 专栏收录该内容

49 篇文章

订阅专栏

本文介绍如何将具有特定时滞的DDE（延迟微分方程）模型转换为一阶和二阶常时滞系统，并通过Matlab的dde23函数进行求解。首先演示了将原始DDE方程简化为y1' = y1(t-0.1)和y2' = y2(t-0.5)，然后扩展到包含y2' = -2和y4' = -2的二阶系统。

文章目录

具有常时滞的 DDE

具有常时滞的 DDE

举例为如下方程
$\begin{aligned} y_1'(t) &= y_1(t-1) \\ y_2'(t) &= y_1(t-1) + y_2(t-0.2) \\ y_3'(t) &= y_2(t-1) \\ \end{aligned}$

编写时滞代码

%% 测试求解常时滞微分方程
% Author: Zhao-Jichao
% Date: 2021-07-05
clear
clc

%% Define Time-Delay
lags = [1 0.2];

tspan = [0 5];
sol = dde23(@ddefun, lags, @history, tspan);

%% Draw Results
plot(sol.x,sol.y,'-o')
xlabel('Time t');
ylabel('Solution y');
legend('y_1','y_2','y_3','Location','NorthWest');

%% DDE Function
function dydt = ddefun(t,y,Z) % equation being solved
  ylag1 = Z(:,1);
  ylag2 = Z(:,2);

  dydt = [ylag1(1); 
          ylag1(1)+ylag2(2); 
          y(2)];
end
%-------------------------------------------
function s = history(t) % history function for t <= 0
  s = ones(3,1);
end
%-------------------------------------------

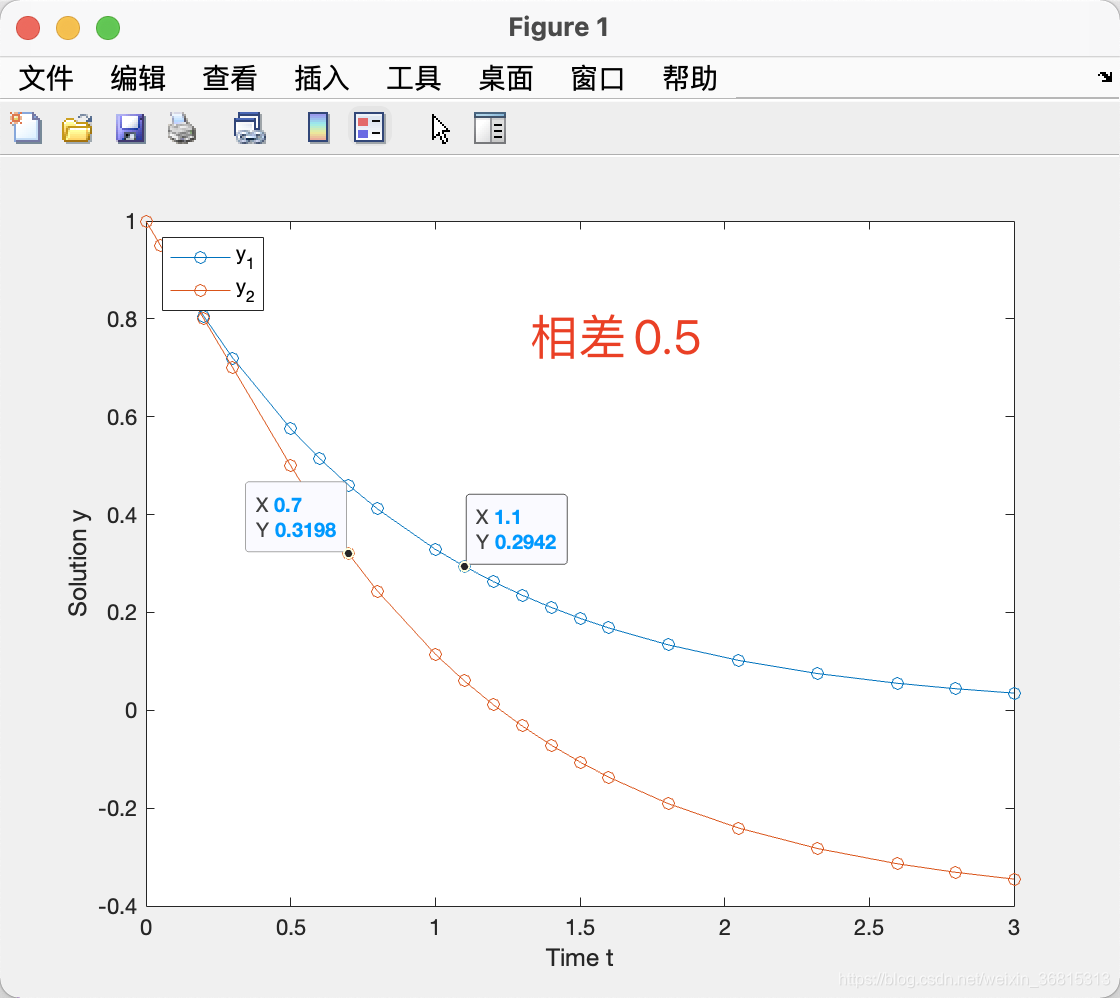
在这里插入图片描述

修改成自用的一阶系统微分方程

$\begin{aligned} y_1'&=y_1(t-0.1) \\ y_2'&=y_2(t-0.5) \\ \end{aligned}$

写成了两个并列的形式，方便对比最终的效果。

代码如下

%% 测试求解常时滞微分方程
% Author: Zhao-Jichao
% Date: 2021-07-05
clear
clc

%% Define Time-Delay
lags = [0.1 0.5];

tspan = [0 5];
sol = dde23(@ddefun, lags, @history, tspan);

%% Draw Results
plot(sol.x,sol.y,'-o')
xlabel('Time t');
ylabel('Solution y');
legend('y_1','y_2','y_3','Location','NorthWest');

%% DDE Function
function dydt = ddefun(t,y,Z) % equation being solved
  ylag1 = Z(:,1);
  ylag2 = Z(:,2);

  dydt = [-ylag1(2); 
          -ylag2(2)];
end
%-------------------------------------------
function s = history(t) % history function for t <= 0
  s = ones(2,1);
end
%-------------------------------------------

在这里插入图片描述

再改一个二阶的

方程为：
$\begin{aligned} y_1' &= y_2(t-0.1) \\ y_2' &= -2 \\ y_3' &= y_4(t-0.5) \\ y_4' &= -2 \\ \end{aligned}$

%% 测试求解常时滞微分方程
% Author: Zhao-Jichao
% Date: 2021-07-05
clear
clc

%% Define Time-Delay
lags = [0.1 0.5];

tspan = [0 3];
sol = dde23(@ddefun, lags, @history, tspan);

%% Draw Results
plot(sol.x,sol.y)
xlabel('Time t');
ylabel('Solution y');
legend('y_1','y_2','y_3','y_4','Location','NorthWest');

%% DDE Function
function dydt = ddefun(t,y,Z) % equation being solved
  ylag1 = Z(:,1);
  ylag2 = Z(:,2);

  dydt = [ylag1(2); 
          -2;
          ylag2(4); 
          -2;];
end
%-------------------------------------------
function s = history(t) % history function for t <= 0
  s = ones(4,1);
end
%-------------------------------------------

在这里插入图片描述