原文:Lidar Odometry and Mapping in Real-time
简介:
-提出了一种低速、低计算量的算法
-将定位问题划分为定位问题和映射问题
-有两种算法:1:高频低精度用来估计雷达速度 2.运行速度低精度高的点云匹配和配对
-当有imu时,可以使用imu用来解决高频运动(非必要)
-需要提取尖锐的边和平面,平且用于匹配边缘线段和平面片
-在计算映射时,通过检验对应局部点簇的集合分布的特征向量和特征值来确定相应关系
-解决往分解问题之间欧就可以通过ICP问题求解
-采用并行计算结构,保证实时性,
-因为运动估计的频率足够高,地图有足够的精度、合并特征点。
相关:
-当雷达频率远高于外部运动,雷达内部的运动畸变可以忽略
-文中提出了种两步去除噪声方法:基于ICP估计速度、在使用估计出来的速度补偿运动畸变。但是使用雷达估计的速度,在扫描过低时误差较大,需要其他传感器提供速度测量值来去除误差(比如VIO)。当存在GPS/INS和轮式里程计时,通常使用扩展kalman和粒子滤波器求解里程。
预设条件
-
雷达的速度和角度是一直平滑且连续的
-
使用IMU
-
k : 表 示 扫 表 扫 描 周 期 , k ∈ Z + , P k : 表 示 在 周 期 k 内 接 收 到 的 所 有 点 k:表示扫表扫描周期,k\in Z^+,P_k:表示在周期k内接收到的所有点 k:表示扫表扫描周期,k∈Z+,Pk:表示在周期k内接收到的所有点
-
{ } : 表 示 坐 标 系 , { L } : 雷 达 坐 标 系 , 中 心 为 雷 达 的 几 何 中 心 , x : 指 向 左 边 , i ∈ P k , y : 指 向 上 方 z : 指 向 前 方 , 点 i 在 雷 达 坐 标 系 表 示 为 X k , i L { W } : 世 界 坐 标 系 : { L } : 的 初 始 坐 标 , i ∈ P k , 点 i 在 世 界 坐 标 系 表 示 为 X k , i W \{\}:表示坐标系,\\ \{L\}:雷达坐标系,中心为雷达的几何中心,x:指向左边,i\in P_k,y:指向上方 z:指向前方,点i在雷达坐标系表示为X^L_{k,i}\\ \{W\}:世界坐标系:\{L\}:的初始坐标,i\in P_k,点i在世界坐标系表示为X^W_{k,i} {}:表示坐标系,{L}:雷达坐标系,中心为雷达的几何中心,x:指向左边,i∈Pk,y:指向上方z:指向前方,点i在雷达坐标系表示为Xk,iL{W}:世界坐标系:{L}:的初始坐标,i∈Pk,点i在世界坐标系表示为Xk,iW

-
问题假设:给定点云 P k , k ∈ Z + P_k,k\in Z^+ Pk,k∈Z+计算激光雷达在每次扫描过程中的运动,并使用 P k P_k Pk建立一张扫描过的地图。
系统概述
- 雷达
Hokuyo UTM-30LX:
| 属性 | 数值 |
|---|---|
| 范围 | 180 。 : ^。: 。:-90~90 |
| 扫描速度 | 40线/秒 |
| 分辨率 | 0.25 |
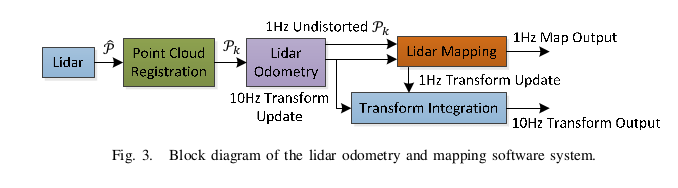
lidar:雷达
Point Cloud Registration:雷达点云匹配
lidar Odometry:雷达里程计
lidar Mapping:雷达建图/映射
transform integration:积分
雷达里程计
- 特帧点提取
-
如何选择特征点?(具有尖锐边或者平面面片)
i ∈ P k i \in P_k i∈Pk
S : 点 i S:点i S:点i在同一雷达扫描期间的连续点集,因为雷达会顺时针在逆时针旋转,所以雷达会包含点i每侧的信息,且两点之间的间隔为0.25 -
曲面平滑度公式
S : 点 i S:点i S:点i在同一雷达扫描期间的连续点集
c : 平 滑 度 c:平滑度 c:平滑度
X k , i L : i 坐 标 在 k 次 扫 描 的 点 集 X_{k,i}^L:i坐标在k次扫描的点集 Xk,iL:i坐标在k次扫描的点集c = 1 ∣ S ∣ ∗ ∣ ∣ X k , i L ∣ ∣ ∣ ∣ ∑ j ∈ S , j ≠ i ( X k , i L − X k , j L ) ∣ ∣ c=\frac{1}{|S|*||X_{k,i}^L||}||\sum_{j\in S,j\neq i}(X^L_{k,i}-X^L_{k,j})|| c=∣S∣∗∣∣Xk,iL∣∣1∣∣j∈S,j=i∑(Xk,iL−Xk,jL)∣∣
-
edge points:C的最大值,边缘点
-
planar points:C的最小值,平面点
-
将一次扫描分为4个区域,每个区域最多可提供2个edge points和4个planar points
-
当点的数量没有达到最大数量,可以通过设置指定阈值获取特征点
-
为了避免旋转特征点周围的点被选中,或选中局部平面,如下图:这些点并不可靠

(a):
A:位于与激光束(橙色虚线)成一定角度的曲面片
B:点B位于大致平行于曲面的曲面片上激光束。我们将B视为不可靠的激光返回,而不将其选为a特征点,
(B):
A:位于݆遮挡区域的边界(橙色虚线段),并可检测为边缘点。但是,如果从不同的角度,遮挡区域会发生变化并变得可见。文中不选则此类点作为特征点。 -
为了解决不合理的特征点,重新约束的集合 S : S: S: 仅当S未形成大致平行于激光束的曲面片,且S中没有遮挡见图(b):B
- 特征点匹配

-
t k : 雷 达 k 次 扫 描 开 始 的 扫 描 时 间 P k : 雷 达 k 次 扫 描 到 的 雷 达 点 P ‾ k : 重 投 影 到 世 界 坐 标 系 的 雷 达 位 置 , 时 间 为 t k + 1 P k + 1 : 新 一 帧 雷 达 扫 描 t_k:雷达k次扫描开始的扫描时间\\ P_k:雷达k次扫描到的雷达点\\ \overline P_k:重投影到世界坐标系的雷达位置,时间为t_{k+1}\\ P_{k+1}:新一帧雷达扫描 tk:雷达k次扫描开始的扫描时间Pk:雷达k次扫描到的雷达点Pk:重投影到世界坐标系的雷达位置,时间为tk+1Pk+1:新一帧雷达扫描
使 用 P k + 1 与 P ‾ k 估 计 相 机 运 动 使用P_{k+1}与\overline P_k估计相机运动 使用Pk+1与Pk估计相机运动
(1):对于 P k + 1 P_{k+1} Pk+1使用第一节介绍的方法找到雷达的特征点:
ξ k + 1 : 边 缘 特 征 点 集 , H k + 1 : 平 面 特 征 点 集 \xi_{k+1}:边缘特征点集,H_{k+1}:平面特征点集 ξk+1:边缘特征点集,Hk+1:平面特征点集
(2):从 P ‾ k \overline P_k Pk查找 ξ k + 1 , H k + 1 : \xi_{k+1},H_{k+1}: ξk+1,Hk+1:的对应值。- 因为在一开始扫描时 ξ k + 1 , H k + 1 \xi_{k+1},H_{k+1} ξk+1,Hk+1为空,并且随时间增加,所以进行迭代求解
- ξ k + 1 , H k + 1 \xi_{k+1},H_{k+1} ξk+1,Hk+1的数值需要映射到到以 t k + 1 t_{k+1} tk+1为原点的局部坐标系 ξ k + 1 ′ , H k + 1 ′ \xi_{k+1}', H_{k+1}' ξk+1′,Hk+1′
- 对于 ξ k + 1 ′ , H k + 1 ′ \xi_{k+1}', H_{k+1}' ξk+1′,Hk+1′中的每一个值,在 P ‾ k \overline P_k Pk查找对应值
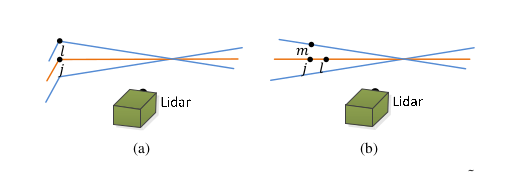
(a)在 P ‾ k \overline P_k Pk找到边缘线,作为 ξ k + 1 ′ \xi_{k+1}' ξk+1′的边缘点对应关系
(b)在 P ‾ k \overline P_k Pk找到指定平面,作为 ξ k + 1 ′ \xi_{k+1}' ξk+1′的平面点对应关系- j: ξ k + 1 ′ \xi_{k+1}' ξk+1′特征点对应 P ‾ k \overline P_k Pk中最临近点,
- 橙色线表示j对应的雷达光束
- 蓝色线表示连续两次扫描
- 在 ( a ) (a) (a), l l l:为了找到边缘线需要找到点 l l l,在蓝线上,边缘点对应关系用 ( j , l ) (j,l) (j,l)表示
- 在 ( b ) (b) (b)中,需要找到m在蓝线上,找到 l l l在橙线上,对应关系用 ( j , l , m ) (j,l,m) (j,l,m)表示
(3):找到边缘线(指定参数说明见上图)
- <1>: i ∈ ξ k + 1 ′ i\in\xi_{k+1}' i∈ξk+1′,找到与其最相近的点 j ∈ P ‾ k j\in\overline P_k j∈Pk
- <2>:l:为包含j的两个扫描连续扫描中与i最近的 l ∈ P k + 1 l\in P_{k+1} l∈Pk+1,得到边缘线 ( j , l ) (j,l) (j,l)
- <3>:使用曲率公式计算确保 j , l j,l j,l均为局部曲面特征点,并且确保j,l不再同一个扫描线上(只有一个例外,边缘线在扫描平面上。如果是这样,则边缘线退化并在扫描平面上显示为一条直线,所以不应首先提取边缘线)。
(4):找到平面补丁,作为量平面之间的映射关系
- <1>: i ∈ H k + 1 ′ ′ i\in H_{k+1}'' i∈Hk+1′′,找到与其最相近的点 j ∈ P ‾ k j\in\overline P_k j∈Pk
- <2>:找到 j j j对应的雷达光束 l ∈ P k + 1 l\in P_{k+1} l∈Pk+1,
- <3>:为了保证 l , m , j l,m,j l,m,j三点不共线,令m在同一激光的蓝线上,l,在橙线上
- <4>:使用曲率公式计算确保 j , l j,l j,l均为局部平面面特征点
- 雷达位姿估计
-
点到直线距离方程:
i ∈ ξ k + 1 ′ ; ( j , l ) ∈ P ‾ k i\in\xi_{k+1}';(j,l)\in\overline P_k i∈ξk+1′;(j,l)∈Pk为对应的边缘线
X k + 1 , i L : i 在 雷 达 坐 标 系 下 的 值 X^L_{k+1,i}:i在雷达坐标系下的值 Xk+1,iL:i在雷达坐标系下的值
X k , j L : j 在 雷 达 坐 标 系 下 的 值 X^L_{k,j}:j在雷达坐标系下的值 Xk,jL:j在雷达坐标系下的值
X k , l L : l 在 雷 达 坐 标 系 下 的 值 X^L_{k,l}:l在雷达坐标系下的值 Xk,lL:l在雷达坐标系下的值
d ξ = ∣ ( X k + 1 , i L − X k , j L ) × ( ( X k + 1 , i L − X k , l L ) ∣ ∣ X k , j L − X k , l L ∣ d\xi=\frac{|(X^L_{k+1,i}-X^L_{k,j})×((X^L_{k+1,i}-X^L_{k,l})|}{|X^L_{k,j}-X^L_{k,l}|} dξ=∣Xk,jL−Xk,lL∣∣(Xk+1,iL−Xk,jL)×((Xk+1,iL−Xk,lL)∣ -
点到平面距离方程
X k , m L : m 在 雷 达 坐 标 系 下 的 值 X^L_{k,m}:m在雷达坐标系下的值 Xk,mL:m在雷达坐标系下的值:
i ∈ H k + 1 ′ ; ( j , l , m ) ∈ P ‾ k i\in H_{k+1}';(j,l,m)\in\overline P_k i∈Hk+1′;(j,l,m)∈Pk为对应的边缘线
X k + 1 , i L : i 在 雷 达 坐 标 系 下 的 值 X^L_{k+1,i}:i在雷达坐标系下的值 Xk+1,iL:i在雷达坐标系下的值
X k , j L : j 在 雷 达 坐 标 系 下 的 值 X^L_{k,j}:j在雷达坐标系下的值 Xk,jL:j在雷达坐标系下的值
X k , l L : l 在 雷 达 坐 标 系 下 的 值 X^L_{k,l}:l在雷达坐标系下的值 Xk,lL:l在雷达坐标系下的值
d H = [ X k + 1 , i L − X k , j L ( X k , j L − X k , l L ) × ( X k , j L − X k , m L ) ] ∣ ( X k , j L − X k , l L ) × ( X k , j L − X k , m L ) ∣ d_H=\frac{\left[\begin{matrix}X^L_{k+1,i}-X^L_{k,j}\\(X^L_{k,j}-X^L_{k,l})×(X^L_{k,j}-X^L_{k,m})\end{matrix}\right]}{|(X^L_{k,j}-X^L_{k,l})×(X^L_{k,j}-X^L_{k,m})|} dH=∣(Xk,jL−Xk,lL)×(Xk,jL−Xk,mL)∣[Xk+1,iL−Xk,jL(Xk,jL−Xk,lL)×(Xk,jL−Xk,mL)] -
这里雷达的速度和加速度模型均为常量
t : 时 间 戳 t:时间戳 t:时间戳
t k + 1 : 当 前 扫 描 开 始 时 间 t_{k+1}:当前扫描开始时间 tk+1:当前扫描开始时间
T k + 1 L = [ t x , t y , t z , θ x , θ y , θ z ] : t k + 1 到 t 的 转 换 矩 阵 T_{k+1}^L=[t_x,t_y,t_z,\theta_x,\theta_y,\theta_z]:t_{k+1}到t的转换矩阵 Tk+1L=[tx,ty,tz,θx,θy,θz]:tk+1到t的转换矩阵
t : 位 移 , θ 指 定 轴 旋 转 , 遵 守 右 手 定 则 t:位移,\theta 指定轴旋转,遵守右手定则 t:位移,θ指定轴旋转,遵守右手定则
给 定 点 i ∈ P k + 1 , t i 为 其 时 间 戳 , T k + 1 , i L : 为 [ t k + 1 , t i ] 之 间 的 转 换 矩 阵 , 在 通 过 线 性 差 值 计 算 T k + 1 L 给定点i\in P_{k+1},t_i为其时间戳,T^L_{k+1,i}:为[t_{k+1},t_i]之间的转换矩阵,在通过线性差值计算T^L_{k+1} 给定点i∈Pk+1,ti为其时间戳,Tk+1,iL:为[tk+1,ti]之间的转换矩阵,在通过线性差值计算Tk+1L
T k + 1 , i L = t i − t k + 1 t − t k + 1 T k + 1 L T^L_{k+1,i}=\frac{t_i-t_{k+1}}{t-t_{k+1}}T^L_{k+1} Tk+1,iL=t−tk+1ti−tk+1Tk+1L -
从上式再得到
ξ k + 1 , H k + 1 \xi_{k+1},H_{k+1} ξk+1,Hk+1:边缘点集和平面特征点集
ξ k + 1 ′ , H k + 1 ′ \xi_{k+1}',H_{k+1}' ξk+1′,Hk+1′:特征点映射到 k + 1 k+1 k+1次扫描开始时间 t k + 1 t_{k+1} tk+1
得到如下公式:
X k + 1 , i L : i ∈ ξ k + 1 / H k + 1 X^L_{k+1,i}:i\in \xi_{k+1}/H_{k+1} Xk+1,iL:i∈ξk+1/Hk+1
T k + 1 , i L ( a : b ) : T k + 1 , i L 表 示 第 a 到 b 行 T^L_{k+1,i}(a:b):T^L_{k+1,i}表示第a到b行 Tk+1,iL(a:b):Tk+1,iL表示第a到b行
X k + 1 , i ′ L : i 的 对 应 点 在 ξ k + 1 ′ / H k + 1 ′ X'^L_{k+1,i}:i的对应点在\xi_{k+1}'/H_{k+1}' Xk+1,i′L:i的对应点在ξk+1′/Hk+1′
X k + 1 , i L = R X k + 1 , i ′ L + T k + 1 , i L ( 1 : 3 ) X^L_{k+1,i}=RX'^L_{k+1,i}+T^L_{k+1,i}(1:3) Xk+1,iL=RXk+1,i′L+Tk+1,iL(1:3) -
R = I + w sin θ + w 2 ( 1 − cos θ ) : 旋 转 矩 阵 ( 根 据 罗 德 里 格 旋 转 公 式 得 到 ) R=I+w\sin\theta+w^2(1-\cos\theta):旋转矩阵(根据罗德里格旋转公式得到) R=I+wsinθ+w2(1−cosθ):旋转矩阵(根据罗德里格旋转公式得到)
θ = ∣ ∣ T k + 1 , i L ( 4 : 6 ) ∣ ∣ \theta=||T^L_{k+1,i}(4:6)|| θ=∣∣Tk+1,iL(4:6)∣∣
w = T k + 1 , i L ( 4 : 6 ) ∣ ∣ T k + 1 , i L ( 4 : 6 ) ∣ ∣ w=\frac{T^L_{k+1,i}(4:6)}{||T^L_{k+1,i}(4:6)||} w=∣∣Tk+1,iL(4:6)∣∣Tk+1,iL(4:6) -
通过点到平面的距离公式和点到线的距离公式构建最小二乘,在利用信赖区域法联合求解,得到姿态的最优解。
ξ k + 1 与 ξ k + 1 ′ \xi_{k+1}与\xi_{k+1}' ξk+1与ξk+1′对应点构建的最小二乘为(9):
f ξ ( X k + 1 , i L , T k + 1 L ) = d ξ , i ∈ ξ k + 1 f_\xi(X^L_{k+1,i},T^L_{k+1})=d_\xi,i\in \xi_{k+1} fξ(Xk+1,iL,Tk+1L)=dξ,i∈ξk+1
H k + 1 与 H k + 1 ′ H_{k+1}与H_{k+1}' Hk+1与Hk+1′对应点构建的最小二乘为(10):
f H ( X k + 1 , i L , T k + 1 L ) = d H , i ∈ H k + 1 f_H(X^L_{k+1,i},T^L_{k+1})=d_H,i\in H_{k+1} fH(Xk+1,iL,Tk+1L)=dH,i∈Hk+1
综合上述两式得到(11):
f ( T k + 1 L ) = d T k + 1 L − ( J T J + λ d i a g ( J T J ) ) − 1 J T d − > T k + 1 L f(T^L_{k+1})=d\\ T^L_{k+1}-(J^TJ+\lambda diag(J^TJ))^{-1}J^Td->T^L_{k+1} f(Tk+1L)=dTk+1L−(JTJ+λdiag(JTJ))−1JTd−>Tk+1L
- 雷达里程计算方法
(1):
P
‾
k
,
P
k
+
1
,
T
k
+
1
L
\overline P_k,P_{k+1},T^L_{k+1}
Pk,Pk+1,Tk+1L
(2):
P
‾
k
+
1
,
最
新
的
T
k
+
1
L
\overline P_{k+1},最新的T_{k+1}^L
Pk+1,最新的Tk+1L
(3):
T
k
+
1
L
T^L_{k+1}
Tk+1L
(4):
ξ
k
+
1
\xi_{k+1}
ξk+1
(5):
H
k
+
1
H_{k+1}
Hk+1
(6):
P
k
+
1
P_{k+1}
Pk+1
(7):
f
(
T
k
+
1
L
)
=
d
f(T^L_{k+1})=d
f(Tk+1L)=d
(8):
T
k
+
1
L
−
(
J
T
J
+
λ
d
i
a
g
(
J
T
J
)
)
−
1
J
T
d
−
>
T
k
+
1
L
T^L_{k+1}-(J^TJ+\lambda diag(J^TJ))^{-1}J^Td->T^L_{k+1}
Tk+1L−(JTJ+λdiag(JTJ))−1JTd−>Tk+1L
(9):
P
‾
k
+
1
\overline P_{k+1}
Pk+1
(10):
T
k
+
1
L
T^L_{k+1}
Tk+1L
输入:(1)
输出:(2)
begin
if 本次扫描刚开始
式(3)=0
end
在式(6)中边缘点和平面特征点(4),(5)
for 迭代计算 do
for 对于每一个在式(4)中边缘点 do
找到边缘线作为对应关系,然后计算点到直线的距离,让后存入栈内供式(7)使用
end
for 每一个在时(5)中的平面点 do
找到每一个平面点对应的相应平面,然后计算点到平面的最小句子,压入栈 供式(7)使用
end
计算式(7)每行的双平方权重
迭代更新式(3)通过式(8)
if 非线性迭代收敛 then
break
end
end
if 本次扫描的最后一帧 then
重映射式(6)中的所有点到t_(k+2),得到新的点集(9),并且返回(9)(10)
end
else
返回更新值(3)
end
endconverges
雷达建图(映射)
-
每次扫描仅调用一次
-
每次扫描结束后: P ‾ k + 1 , T k + 1 L \overline P_{k+1},T^L_{k+1} Pk+1,Tk+1L [ t k + 1 , t k + 2 ] [t_{k+1},t_{k+2}] [tk+1,tk+2]之间的连续运动。
-
mapping 就是将 P ‾ k + 1 \overline P_{k+1} Pk+1映射到 { W } \{W\} {W}世界坐标系

Q K : 直 到 扫 描 k 之 前 , 点 云 上 的 地 图 Q_K:直到扫描k之前,点云上的地图 QK:直到扫描k之前,点云上的地图
T k W : 雷 达 在 k 次 之 前 , 在 地 图 上 的 位 姿 T_k^W:雷达在k次之前,在地图上的位姿 TkW:雷达在k次之前,在地图上的位姿
t k + 1 : 在 k 次 扫 描 结 束 时 的 时 间 t_{k+1}:在k次扫描结束时的时间 tk+1:在k次扫描结束时的时间
Q ‾ k + 1 : P ‾ k + 1 映 射 到 时 世 界 坐 标 系 { W } \overline Q_{k+1}:\overline P_{k+1}映射到时世界坐标系\{W\} Qk+1:Pk+1映射到时世界坐标系{W} -
算法:地图映射将: T k W 从 t k + 1 T_k^W从t_{k+1} TkW从tk+1扩展到 t k + 2 t_{k+2} tk+2,获得新的 T k + 1 W T_{k+1}^W Tk+1W,并将 P ‾ k + 1 \overline P_{k+1} Pk+1映射到时世界坐标系 { W } \{W\} {W},得到 Q ‾ k + 1 \overline Q_{k+1} Qk+1,在用 Q ‾ k + 1 \overline Q_{k+1} Qk+1与 Q k Q_k Qk进行优化操作得到雷达位姿 T k + 1 W T^W_{k+1} Tk+1W。
-
特征点的提取与与雷达状态估计与上边状态估计一致,但是特征点是状态估计时的10倍
-
存储 10 m 3 10m^3 10m3的大小的点云到map: Q k Q_k Qk
-
Q k Q_k Qk中,与 Q ‾ k + 1 \overline Q_{k+1} Qk+1相关的部分,存储在一个3D KD树结构中,
-
S ′ S' S′: Q k Q_k Qk中特征点周围的点集
-
S ′ S' S′对于边缘点,只包含边缘线上的点,对于平面点只保留平面片上的点
-
M : M: M: S ′ S' S′的协防差矩阵
-
V , E V,E V,E: M M M的特征值和特征向量
-
当 S ′ S' S′中分布位于边缘线,V中有一个特征值显著大于其余其他两个,E中对应最大值的特征向量表示边缘线的方向。
-
当 S ′ S' S′中分布位于平面片上,V有有两个大的特征向量和一个较小的,E中对应最小值的特征向量表示面片的方向
-
边缘线的位置和平面面片的位置由 S ′ S' S′的几何中心确定
-
计算距离进行优化:选择两个点在边缘线,选择三个点在平面面片,在使用相应方式计算距离,然后构建最小二乘,在进行 Q ‾ k + 1 \overline Q_{k+1} Qk+1与地图点使用信赖区域法求解,为了使用这些点均匀分布需要进行体素滤波5cm的立方体。

蓝 色 区 域 为 雷 达 到 地 图 ( 起 始 点 ) 的 位 姿 : T k W 蓝色区域为雷达到地图(起始点)的位姿:T_k^W 蓝色区域为雷达到地图(起始点)的位姿:TkW
橙 色 区 域 为 雷 达 进 行 一 次 扫 描 估 计 的 位 姿 : T k + 1 L 橙色区域为雷达进行一次扫描估计的位姿:T_{k+1}^L 橙色区域为雷达进行一次扫描估计的位姿:Tk+1L
























 2678
2678

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








