机器学习实战之路 —— 1 线性回归 (一)

近期自己准备将之前在机器学习方面做的一些学习及研究工作，重新稍加整理成稿发出来，权当记录分享。俗话说，好记性不如烂笔头，有时候自己理解是一个层次，而写出来给别人看，往往需要站在受众的角度去思考，进而希望更好的传达自己的观点和想法，所以在文章构思及落笔成文时，已经加深了自己对原本问题和相关知识的理解，这是比仅仅自己理解更深入的一个层次。回顾自己求学及工作中整理撰写各类论文及报告时，莫不如此。分享不仅是对自己过往学习的一个回顾，一定程度上也是驱动进一步学习的动力。

1. 线性回归

回归问题和分类问题的区别仅仅在于设定的目标值得类型不同。分类设定的目标值是离散的，意义是“类别”；而回归设定的目标值是连续的，意义是某种“数值”。由于仅仅是目标值不同，所以对于大部门的机器学习模型而言，一般都有对应的“分类版”模型实现和“回归版”模型实现。相对应的分类模型和回归模型在实现思路上非常相近，一般而言，两者的主要区别在于：
*目标数值的类型不同（离散值 vs 连续值）
*损失函数设计不同
*评估指标选择不同
——《机器学习之路》$P_{61}$

线性模型形式简单、易于建模，但却蕴涵着机器学习中一些重要的基本思想。许多功能更为强大的非线性模型 (nonlinear model)可在线性模型的基础上通过引入层级结构或高维映射而得。此外，由于 ω 直观表达了各属性在预测中的重要性，因此线性模型有很好的可解释性 (comprehensibility)。
——《机器学习-周志华》$P_{53}$

优点：结果易于理解，计算上不复杂。
缺点：对非线性的数据拟合不好。
适用数据类型：数值型和标称型数据。
——《机器学习实战》$P_{136}$

回归的一般方法：

1. 收集数据：采用任意方法收集数据。
2. 准备数据：回归需要数值型数据，标称型数据将被转成二值型数据。
3. 分析数据：绘出数据的可视化二维图将有助于对数据做出理解和分析，在采用缩减法求得新回归系数之后, 可以将新拟合线绘在图上作为对比。
4. 训练算法：找到回归系数。
5. 测试算法：使用$R^2$或者预测值和数据的拟合度，来分析模型的效果。
6. 使用算法：使用回归，可以在给定输入的时候预测出一个数值，这是对分类方法的提升，因为这样可以预测连续型数据而不仅仅是离散的类别标签。
   ——《机器学习实战》$P_{137}$

2. 标准线性回归

2.1 方程组求解

在此首先将以线性回归为例，介绍回归算法和模型。回归分析是迄今为止数值型数据建模最常用的方法，可以适用几乎所有的数据，且提供了变量与结果之间强度与大小的估计。在线性回归的学习过程中，在此也将会展开论述其中的推导过程。

对于给定数据集 D = { ( x 1 , y 1 ) , ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . . . . , ( x m , y m ) } D=\{ (x_1,y_1),(x_1,y_1),(x_2,y_2),......,(x_m,y_m)\} D={(x1​,y1​),(x1​,y1​),(x2​,y2​),......,(xm​,ym​)}，其中$x_i=(x_{i}1,x_{i}1,......,x_{i}d)$, $y_i\in R$，线性回归(linear regression)试图学得一个线性模型$f(x_i)=\omega \ast x_i+b$，以尽可能准确地预测实值输出标记$f(x_i)\approx y_i$。

回归任务中常使用均方误差来衡量 f(x) 与 y 之间的差别。使均方误差最小化得到的 ω, b 即我们所求。基于均方误差来进行模型求解的方法称为最小二乘法：

$$\begin{array}{rl}L(\omega ,b)& =\sum _{i=1}^m(y_i-f(x_i){)}^2\\ & =\sum _{i=1}^m(y_i-(\omega \ast x_i+b){)}^2(2.1)\end{array}$$
L(ω,b)是关于ω和b的凸函数，当它关于ω和b导数均为0时，可得到ω和b的最优解。

求解 b，将L(ω,b)对b求偏导令其等于零：
$$\begin{array}{rl}\frac{\partial L(\omega ,b)}{\partial b}=2\ast (\sum _{i=1}^m(y_i-(\omega \ast x_i+b)))\ast (-1)& =0\\ \sum _{i=1}^m{y}_i& =\sum _{i=1}^m(\omega \ast x_i+b)\\ \sum _{i=1}^m{y}_i& =\omega \sum _{i=1}^m{x}_i+m\ast b\\ \frac{1}{m}\sum _{i=1}^m{y}_i& =\frac{1}{m}\ast \omega \sum _{i=1}^m{x}_i+b\\ \overline{y_i}& =\omega \ast \overline{x_i}+b\\ b& =\overline{y_i}-\omega \ast \overline{x_i}\end{array}$$

b的表达式为:
$$b=\overline{y_i}-\omega \ast \overline{x_i}(2.2)$$
其中：$\overline{x}=\frac{1}{m}\ast {\sum }_{i=1}^m{x}_i$，$\overline{y}=\frac{1}{m}\ast {\sum }_{i=1}^m{y}_i$
求解ω，将L(ω,b)对ω求导令其等于零：
$$\begin{array}{rl}\frac{\partial L(\omega ,b)}{\partial \omega }=2\ast (\sum _{i=1}^m(y_i-(\omega \ast x_i+b)))\ast (-x_i)& =0\\ (\sum _{i=1}^m(y_i\ast x_i))& =\omega \sum _{i=1}^m{x}_i^2+\sum _{i=1}^{m}b\ast x_i\end{array}$$
将$b=\overline{y_i}-\omega \ast \overline{x_i}$带入上式：
$$\begin{array}{rl}\sum _{i=1}^m{y}_i\ast x_i& =\omega \sum _{i=1}^m{x}_i^2+\sum _{i=1}^m(\overline{y_i}-\omega \ast \overline{x_i})\ast x_i\\ \sum _{i=1}^m{y}_i\ast x_i& =\omega \sum _{i=1}^m{x}_i^2+\overline{y_i}\sum _{i=1}^m{x}_i-\omega \ast \overline{x_i}\sum _{i=1}^m{x}_i\\ \omega \ast (\sum _{i=1}^m{x}_i^2-\overline{x_i}\sum _{i=1}^m{x}_i)& =\sum _{i=1}^m{y}_i\ast x_i-\overline{y_i}\sum _{i=1}^m{x}_i\\ \omega & =\frac{{\sum }_{i=1}^m{y}_i\ast x_i-\overline{y_i}{\sum }_{i=1}^m{x}_i}{{\sum }_{i=1}^m{x}_i^2-\overline{x_i}{\sum }_{i=1}^m{x}_i}(2.3)\end{array}$$
上式(2.3)中：
$$\begin{array}{rl}\overline{y_i}\sum _{i=1}^m{x}_i& =\frac{1}{m}\sum _{i=1}^m{y}_i\sum _{i=1}^m{x}_i\\ & =\frac{1}{m}\sum _{i=1}^m{x}_i\sum _{i=1}^m{y}_i\\ & =\overline{x_i}\sum _{i=1}^m{y}_i\\ \overline{y_i}\sum _{i=1}^m{x}_i=\overline{x_i}\sum _{i=1}^m{y}_i(2.4)& \end{array}$$
此外：
$$\begin{array}{rl}\overline{y_i}\sum _{i=1}^m{x}_i& =m\ast \frac{1}{m}\ast \overline{y_i}\sum _{i=1}^m{x}_i\\ & =m\ast \overline{y_i}\ast \overline{x_i}\\ & =\sum _{i=1}^m\overline{y_i}\ast \overline{x_i}\\ \overline{y_i}\sum _{i=1}^m{x}_i=\sum _{i=1}^m\overline{y_i}\ast \overline{x_i}(2.5)& \end{array}$$
联立(2.4)和(2.5)，可得式(2.6)及推广(2.7)：
$$\begin{array}{r}\overline{y_i}\sum _{i=1}^m{x}_i=\overline{x_i}\sum _{i=1}^m{y}_i=\sum _{i=1}^m\overline{y_i}\ast \overline{x_i}(2.6)\\ \overline{x_i}\sum _{i=1}^m{x}_i=\overline{x_i}\sum _{i=1}^m{x}_i=\sum _{i=1}^m{\overline{x_i}}^2(2.7)\end{array}$$
同样推导可得：
$$\begin{array}{rl}\overline{x_i}\sum _{i=1}^m{x}_i& =\frac{1}{m}\sum _{i=1}^m{x}_i\sum _{i=1}^m{x}_i\\ & =\frac{1}{m}(\sum _{i=1}^m{x}_i{)}^2\\ \overline{x_i}\sum _{i=1}^m{x}_i=\frac{1}{m}(\sum _{i=1}^m{x}_i{)}^2(2.8)& \end{array}$$
将式(2.5) $\overline{y_i}{\sum }_{i=1}^m{x}_i=\overline{x_i}{\sum }_{i=1}^m{y}_i$和式(2.8) $\overline{x_i}{\sum }_{i=1}^m{x}_i=\frac{1}{m}({\sum }_{i=1}^m{x}_i{)}^2$带入式(2.3)即可得式(2.9)：
$$\begin{array}{rl}\omega & =\frac{{\sum }_{i=1}^m{y}_i\ast x_i-\overline{y_i}{\sum }_{i=1}^m{x}_i}{{\sum }_{i=1}^m{x}_i^2-\overline{x_i}{\sum }_{i=1}^m{x}_i}\\ & =\frac{{\sum }_{i=1}^m{y}_i\ast x_i-\overline{x_i}{\sum }_{i=1}^m{y}_i}{{\sum }_{i=1}^m{x}_i^2-\frac{1}{m}({\sum }_{i=1}^m{x}_i{)}^2}\\ & =\frac{{\sum }_{i=1}^m{y}_i\ast (x_i-\overline{x_i})}{{\sum }_{i=1}^m{x}_i^2-\frac{1}{m}({\sum }_{i=1}^m{x}_i{)}^2}(2.9)\end{array}$$
联立ω和b表达式(2.9)，(2.2)，即可得ω，b的第一种表达形式 (2.10)：
$$\begin{array}{rl}\omega & =\frac{{\sum }_{i=1}^m{y}_i\ast (x_i-\overline{x_i})}{{\sum }_{i=1}^m{x}_i^2-\frac{1}{m}({\sum }_{i=1}^m{x}_i{)}^2}b=\overline{y_i}-\omega \ast \overline{x_i}(2.10)\end{array}$$
将$\overline{x}=\frac{1}{m}\ast {\sum }_{i=1}^m{x}_i$和$\overline{y}=\frac{1}{m}\ast {\sum }_{i=1}^m{y}_i$带入式(2.10)，整理即可得ω，b的第二种表达形式(2.11)：
$$\begin{array}{r}\omega =\frac{m\ast {\sum }_{i=1}^m{y}_i\ast x_i-{\sum }_{i=1}^m{y}_i{\sum }_{i=1}^m{x}_i}{m\ast {\sum }_{i=1}^m{x}_i^2-({\sum }_{i=1}^m{x}_i{)}^2}b=\frac{{\sum }_{i=1}^m{x}_i^2{\sum }_{i=1}^m{y}_i-{\sum }_{i=1}^m{x}_i{\sum }_{i=1}^m{x}_i\ast y_i}{m\ast {\sum }_{i=1}^m{x}_i^2-({\sum }_{i=1}^m{x}_i{)}^2}(2.11)\end{array}$$
将式(2.6) 和式(2.7)带入式(2.9)即可得式(2.12)：
$$\begin{array}{rl}\omega & =\frac{{\sum }_{i=1}^m{y}_i\ast x_i-\overline{y_i}{\sum }_{i=1}^m{x}_i}{{\sum }_{i=1}^m{x}_i^2-\overline{x_i}{\sum }_{i=1}^m{x}_i}\\ & =\frac{{\sum }_{i=1}^m{y}_i\ast x_i-\overline{y_i}{\sum }_{i=1}^m{x}_i-\overline{x_i}{\sum }_{i=1}^m{y}_i+{\sum }_{i=1}^m\overline{y_i}\ast \overline{x_i}}{{\sum }_{i=1}^m{x}_i^2-\overline{x_i}{\sum }_{i=1}^m{x}_i-\overline{x_i}{\sum }_{i=1}^m{x}_i+{\sum }_{i=1}^m{\overline{x_i}}^2}\\ & =\frac{{\sum }_{i=1}^m(x_i-\overline{x_i})(y_i-\overline{y_i})}{{\sum }_{i=1}^m(x_i-\overline{x_i}{)}^2}\\ & =\frac{cov(x,y)}{var(x)}(2.12)\end{array}$$
联立可得ω，b的第三种表达形式：
$$\begin{array}{r}\omega =\frac{cov(x,y)}{var(x)}=\frac{{\sum }_{i=1}^m(x_i-\overline{x_i})(y_i-\overline{y_i})}{{\sum }_{i=1}^m(x_i-\overline{x_i}{)}^2}b=\overline{y_i}-\omega \ast \overline{x_i}(2.13)\end{array}$$

2.2 矩阵求解

除了上述方程组的求解方法，还可以利用矩阵方法来求解。对于原拟合函数，同样可写成：
$$\begin{array}{rl}y& =\omega \ast x_i+b\\ & ={\omega }_0+{\omega }_1\ast x\end{array}$$
对于m个样本，则相应的矩阵表达式为：
$$\begin{array}{rl}Y& =X\omega \end{array}$$
式中：
$$\begin{array}{r}Y=\left[\begin{array}{c}{y}_1\\ y_2\\ ⋮\\ y_m\end{array}\right]X=\left[\begin{array}{cc}1& x_1\\ 1& x_2\\ ⋮& \\ 1& x_m\end{array}\right]\omega =\left[\begin{array}{c}{\omega }_0\\ {\omega }_1\end{array}\right]\end{array}$$
进而可得：
$$\begin{array}{rl}L& =\sum _{i=1}^m(y_i-x_i^T\omega {)}^2\\ & =(Y-X\omega {)}^T(Y-X\omega )\\ & =(Y-X\omega {)}^{T}Y-(Y-X\omega )X\omega \\ & =Y^{T}Y-{\omega }^T{X}^{T}Y-Y^{T}X\omega +{\omega }^T{X}^{T}X\omega (2.14)\end{array}$$
根据矩阵求导的几个重要公式及性质：
$$\begin{array}{r}\frac{\partial X^{T}AX}{\partial X}=2AX\frac{\partial X^{T}A}{\partial X}=A\frac{\partial AX}{\partial X}=A^T\end{array}$$
则式对(2.14)求导可得:
$$\begin{array}{rl}\frac{\partial L}{\partial \omega }& =\frac{\partial Y^{T}Y-{\omega }^T{X}^{T}Y-Y^{T}X\omega +{\omega }^T{X}^{T}X\omega }{\partial \omega }\\ & =-2X^{T}Y+2X^{T}X\omega \end{array}$$
令该导数为零，当$X^{T}X$可逆，则有：
$$\begin{array}{rl}-2X^{T}Y+2X^{T}X\omega & =0\\ X^{T}X\omega & =X^{T}Y\\ \omega & =(X^{T}X{)}^{-1}{X}^{T}Y(2.15)\end{array}$$

2.3 模型评估

基于线性回归拟合得到的模型之后，很重要的一点就是如何评估该线性回归模型对给定数据的拟合程度？
关于该问题，在回归算法通常采用决定系数（coefficient ofdetermination）$R^2$来评估。以下给出$R^2$的相关概念定义。
总平方和 $SS{R}_{tot}$：$SS{R}_{tot}={\sum }_{i=1}^m(y_i-\overline{y_i})$
回归平方和$SS{R}_{reg}$：$SS{R}_{reg}={\sum }_{i=1}^m(f(x_i)-\overline{y_i})$
残差平方和$SS{R}_{res}$：$SS{R}_{reg}={\sum }_{i=1}^m(y_i-f(x_i))$
决定系数$R^2$：$R^2=1-\frac{SS{R}_{res}}{SS{R}_{tot}}$
$SS{R}_{res}$表征的是真实数据和回归数据的误差，$SS{R}_{tot}$表征的是真实数据和其平均值的误差，$SS{R}_{res}$一般情况下比 $SS{R}_{tot}$小，其比值一般在0-1之间。当回归拟合越准确，则$SS{R}_{res}$越小，$R^2$越接近于1；当拟合越不准确，则$SS{R}_{res}$越大，$R^2$越接近于0。
$R^2$表征了自变量x对因变量y的解释程度，当自变量引起的变动占总变动的百分比高，则观察点在回归直线附近越密集，也就是回归拟合度越好。

3. 实战

问题描述：
假设某披萨店的披萨价格和披萨直径之间有下列数据关系：

ID	Diameter	Price
1	6	7.0
2	8	9.0
3	10	13.0
4	14	17.5
5	18	18.0

其中 Diameter 为披萨直径，单位为“英寸”；Price 为披萨价格，单位为“美元”。
根据以上训练数据，来预测任一直径的披萨的价格。

要分析该问题，我们首先可以使用 matplotlib 画出数据的散点图，x 轴表示披萨直径，y 轴表示披萨价格。由此可以直观的查看和分析数据信息。

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression

# 读取数据
pizza = pd.read_csv("pizza.csv", index_col='Id')
pizza.head()

# 定义绘图
def runplt():
    plt.figure()
    plt.scatter(dia, price, c='r', marker='o')  # 绘制散点图
    plt.title("Pizza price plotted against diameter")
    plt.xlabel("Diameter")
    plt.ylabel("Price")
    plt.grid(True)
    plt.xlim(0,25)
    plt.ylim(0,25)
    return plt
	
# 获取pizza尺寸、价格数据
dia = pizza.loc[:,'Diameter'].values 
price = pizza.loc[:,'Price'].values

# 绘制散点图
plt = runplt()
plt.show()

绘制得到的数据视图如下：

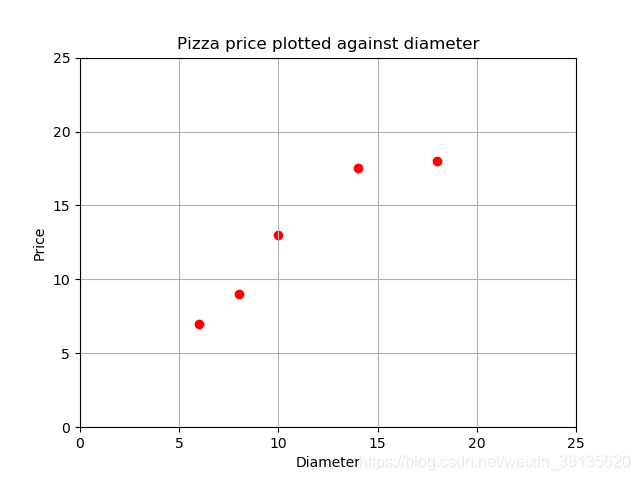
基于以上训练数据散点图可容易看出，其分布具备线性关系，由此我们可以假设披萨的直径和价格关系可用线性回归模型表示： $f(x)=\omega \ast x+b$，这里 x 指披萨的直径，f(x) 为预测的披萨的价格。根据2.1章节的方程组推导公式，求解参数ω，b。
实现代码如下：

# 解法一 公式(2.10) ：
# w = np.sum(price * (dia - np.mean(dia))) / (np.sum(dia**2) - (1/dia.size) * (np.sum(dia))**2)
# b = (1 / dia.size) * np.sum(price - w * dia)

#解法二 公式(2.13)：
variance = np.var(dia, ddof=1)  # 计算方差，doff为贝塞尔（无偏估计）校正系数
covariance = np.cov(dia, price)[0][1]  # 计算协方差
w = covariance / variance
b = np.mean(price) - w * np.mean(dia)
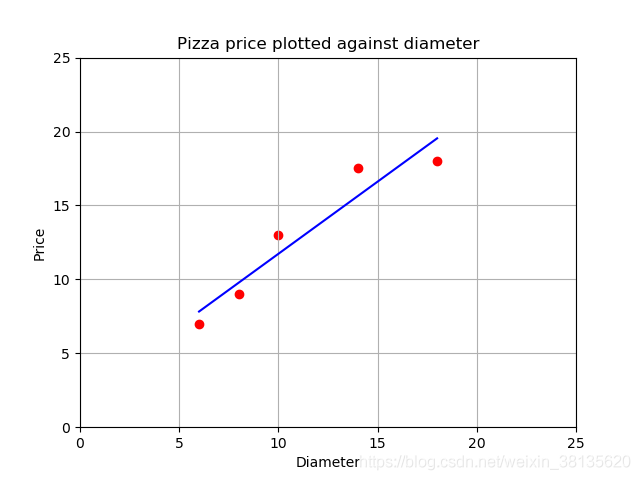
print("w = %f\nb = %f" % (w, b))
y_pred = w * dia + b # 拟合曲线
# 拟合曲线
plt = runplt()
plt.plot(dia, y_pred, 'b-')
plt.show()

输出结果如下：

w= 0.976293
b= 1.965517

绘图如下：

也可以根据2.2章节的矩阵求解推导公式，求解回归系数。

# 解法三：矩阵求解
def standRegres(xArr,yArr):
    xMat = mat(xArr); yMat = mat(yArr).T
    xTx = xMat.T*xMat
    if linalg.det(xTx) == 0.0:
        print("矩阵为奇异矩阵,不能求逆")
        return
    # 计算回归系数
    ws = xTx.I * (xMat.T*yMat)
    return ws
dia1 = np.vstack([np.ones(len(dia)), dia]).T # 增加单位1的首列
regrescoeff = standRegresMatirx(dia1,price)  # 回归系数
print(regrescoeff)

输出结果如下：

 [[1.96551724]
 [0.9762931 ]]

易知矩阵解法和方程组求解获得同样的回归系数。

也可以直接调用sklearn库，使用linear_model中线性回算法模型，关键代码如下：

解法四：sklearn.linear_model 线性回归模型求解
model = LinearRegression() #创建模型
x_train = dia.reshape((-1,1)) # 数据转换成1列
y_train = price
model.fit(x_train,y_train) # 用训练集来训练出线型回归模型
print("回归系数：", model.coef_, "   截距：", model.intercept_)

x_test = [[0], [10], [22]] # 取3个预测值
y_pred2 = model.predict(x_test) # 进行预测
print("预测值:",y_pred2)

plt = runplt()
plt.plot(x_test, y_pred2, 'g-',label='sklearn') #绘制拟合曲线
plt.plot(dia, y_pred, 'b--',label='standRegres')
plt.legend(loc='upper left')
plt.show()

# 模型评估
x_test = [[8], [9], [11], [16], [12]]
y_test = [[11], [8.5], [15], [18], [11]]

print("======== 模型评价 R^2 ========")
print("Training R^2 = ", model.score(x_train, y_train))
print("Test R^2 = ", model.score(x_test, y_test))

输出结果如下：

回归系数： [0.9762931]    截距： 1.965517241379315
预测值: [ 1.96551724 11.72844828 23.44396552]
======== 模型评价 R^2 ========
Training R^2 =  0.9100015964240102
Test R^2 =  0.6620052929422553

由于该回归模型本身基于训练数据集拟合得来，所以可以看到该回归模型对训练数据拟合较好，但对测试数据的拟合程度并没那么好。
输出的绘图如下：

可以看到两条拟合直线重合，即我们之前求解回归系数得到的回归模型与使用sklearn库求出的回归模型是相同的。

4. 参考学习的书目及论文

本人在学习过程中，主要参考的相关书籍等材料在此也列出并标注相应章节，由于本人来自汽车行业，知识技术的学习及理解运用的目的始终是希望围绕联系具体的自身业务领域，所以也给出阅读学习的一些汽车方面相关机器学习的硕博论文以作参考。

1. 机器学习算法视频 - 邹博
2. 《线性回归分析导论》机械工业出版社
3. 《线性代数 - 吴传生》第3章 矩阵的运算
4. 《机器学习实战》第8章 预测数值型数据：回归
5. 《机器学习之路》第2章 机器学习进阶：调试模型
6. 《机器学习 - 周志华》第3章 线性模型
7. 《基于机器学习方法的打车需求量预测研究》魏楷聪 2019 硕士论文 - 第4章 基于线性回归和样条曲线的变化趋势提取

=文档信息=
本学习笔记由博主整理编辑，仅供非商用学习交流使用
由于水平有限，错误和纰漏之处在所难免，欢迎大家交流指正
如本文涉及侵权，请随时留言博主，必妥善处置
版权声明：非商用自由转载-保持署名-注明出处
署名(BY) ：zhudj
文章出处：https://zhudj.blog.csdn.net/