本文探讨了控制系统对单位阶跃信号的响应，重点关注了一阶和二阶系统的性能。二阶系统在欠阻尼情况下的阶跃响应特性包括上升时间、峰值时间和超调量。系统的响应速度与逼近预期响应的程度存在冲突，阻尼比和系统频率影响这些性能指标。此外，高阶系统可以通过二阶系统近似分析，并通过观测调节期间的振荡次数来识别阻尼。对于反馈控制系统，稳态误差取决于开环传递函数的积分器数量，而系统型数与跟踪误差直接相关。
控制系统本质上是时域系统
常见的标准测试信号有单位脉冲信号（测试系统对冲击的抵抗能力），阶跃信号（测试系统对输入的响应能力），斜坡信号和抛物线信号（测试系统对一阶和二阶轨迹的跟随能力）。
二阶系统的性能
一个典型的二阶系统如图所示
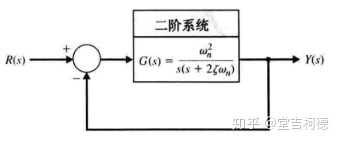
输入输出关系为
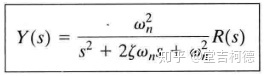
考虑单位脉冲函数的输入（拉普拉斯变换为1），系统输出为
对应的瞬态响应为
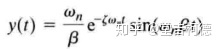
二阶控制系统的典型阶跃响应如下图所示（欠阻尼系统）
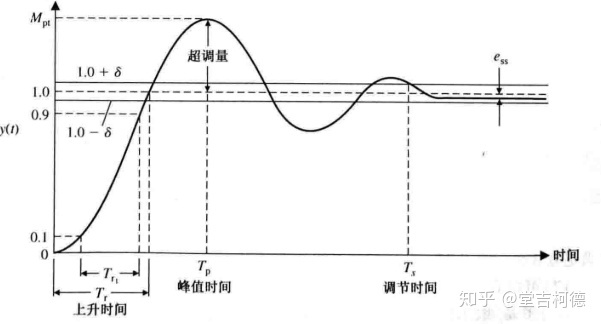
系统的瞬态响应性能主要体现在以下两个方面
- 响应的快速性：由上升时间和峰值时间表征
- 实际相应对预期响应的逼近程度：由超调量和调节时间表征
这些量的计算公式如下，通过公式可以看到系统瞬态响应性能的两个方面是相互冲突的。
一些结论：
- 误差要求为2%时，调节时间约为时间常数的4倍
- 阻尼比越大，超调量越小-->系统对乐器响应的逼近程度越好；同时峰值时间增加-->系统响应的快速性减弱
- 给定阻尼比，当系统频率增加时，系统响应变快，且超调量不变
- 给定系统频率，阻尼比越小，系统响应速度越快，但是逼近程度减小
高阶系统的简化分析
- 具有一堆主导极点的高阶系统，可用和高阶系统具有相同主导极点的二阶系统近似，以避免复杂的运算。
- 系统同时收到零点的影响，具有零点的二阶及更高阶的系统需要另行分析
系统阻尼的简单辨识
二阶系统在调节时间内可观测到的振荡的次数约为
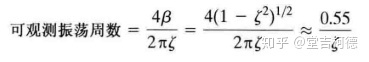
可以以此来对系统阻尼进行粗略辨识。
反馈控制系统的稳态误差
忽略测量噪声和干扰信号时，单位负反馈系统的跟踪误差为
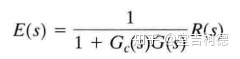
由终值定理得，稳态跟踪误差为
可以看到，稳态误差完全由开环传递函数决定。
若开环传递函数中有N个积分器，则该系统得型数为N
可将阶跃信号视为0次曲线，斜坡信号视为1次曲线，抛物线信号视为2次曲线。
若系统型数大于信号的次幂数，则系统稳态误差为0，若系统型数等于信号的次幂数，则系统稳态误差为常数；若系统型数小于信号的次幂数，则系统稳态误差为无穷大
对应关系如下表。该表中阶跃响应的稳态误差和其他两个信号不同，因为阶跃信号不连续
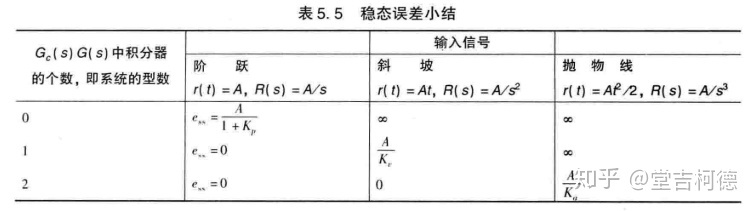
位置误差常数、速度误差常数和加速度误差常数很有规律，分别为
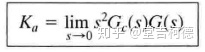
综合性能指标
综合性能指标包括误差平方积分指标，误差绝对值积分指标，时间误差积积分指标，时间误差平方积积分指标
扫一扫
6198
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
