一、RCM和因果图
RCM和因果图是等价的,但是RCM更加准确,因果图更加直观。
二、RCM基本概念
潜在结果指的是一个个体如果接受了某种处理会怎样,也就是指如果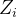 取某种值时(比如1或者0)对应结果
取某种值时(比如1或者0)对应结果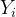 取值会如何。我们用
取值会如何。我们用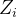 表示个体i的处理,
表示个体i的处理,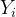 表示个体i的所能观测到的结果变量,
表示个体i的所能观测到的结果变量, 表示个体i的潜在结果(假设对个体的处理只有0或1两种,更多处理时可以进行扩展为多种)。
表示个体i的潜在结果(假设对个体的处理只有0或1两种,更多处理时可以进行扩展为多种)。
个体因果效应:
显然这个个体因果效应是不能计算的,因为不能同时对个体i进行多种操作(我们只能对个体i做一种操作,比如吃药或者不吃药)。幸运的是我们可以通过随机化试验计算平均因果效应。
平均因果效应:

接下来看一下这个公式怎么计算,使用
 表示整体的潜在结果,
表示整体的潜在结果,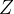 表示整体的取值,
表示整体的取值,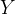 表示整体的观测结果:
表示整体的观测结果:
2式使用的是期望算法的线性展开。
3式用到了随机化,这里有一个强假设,用处理值为1的试验组的期望代替了所有数据潜在结果
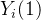 的期望,用处理值为0的对照组的期望代替了所有数据潜在结果
的期望,用处理值为0的对照组的期望代替了所有数据潜在结果
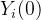 的期望。
的期望。
4式代表的为观测到的期望,所有最后计算转化为了观测数据的计算。
强假设:可以看出上面的计算有一个严重的问题,数据是否随机化的,我们的假设是否能够成立。
在实际中,很多数据都不是随机的,也就是上面的假设不能成立。比如:个体属性(性别),个体处理(是否吸烟),个体结果(是否的癌症)。可以看出性别对癌症是有影响的,不能直接通过吸烟的随机化试验结果代替所有人员吸烟的潜在结果。所以这里面性别是不可忽略的。那
我们的处理方法就是讲个体属性也纳入随机化试验,比如吸烟组同不吸烟组有着相同的男女比例构成。
我们用
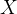 表示整体的属性(信息,混杂因素),则上式就转化成了下式:
表示整体的属性(信息,混杂因素),则上式就转化成了下式:

![=E_{X}[E_{Y(1))}(Y(1)|X)] - E_{X}[E_{Y(0)}(Y(0)|X)] -----2](https://latex.csdn.net/eq?%3DE_%7BX%7D%5BE_%7BY%281%29%29%7D%28Y%281%29%7CX%29%5D%20-%20E_%7BX%7D%5BE_%7BY%280%29%7D%28Y%280%29%7CX%29%5D%20-----2)
![=E_{X}[E_{Y(1)}(Y(1)|X,Z=1)]-E_{X}[E_{Y_(0)}(Y(0)|X,Z=0)] --3](https://latex.csdn.net/eq?%3DE_%7BX%7D%5BE_%7BY%281%29%7D%28Y%281%29%7CX%2CZ%3D1%29%5D-E_%7BX%7D%5BE_%7BY_%280%29%7D%28Y%280%29%7CX%2CZ%3D0%29%5D%20--3)
![=E_{X}[E_{Y}(Y|X,Z=1)]-E_{X}[E_{Y}(Y|X,Z=0)] ---4](https://latex.csdn.net/eq?%3DE_%7BX%7D%5BE_%7BY%7D%28Y%7CX%2CZ%3D1%29%5D-E_%7BX%7D%5BE_%7BY%7D%28Y%7CX%2CZ%3D0%29%5D%20---4)
但是在实际处理中,仍然存在一些问题,通常是由于混杂因素的维度很高,控制相同取值的样本可能数量很少,导致期望估计不准确。针对这一问题,研究者们提出了多种解决方案.常见的方法有基于倾向性得分的估计方法、基于回归的估计方法以及两者相结合的方法。
三、倾向性得分估计
倾向性得分其实是一个降维的过程。
倾向性得分(propensity score
)指的是给定混杂变量X的情况下获得处理Z=1的概率,即P(Z=1|X),可以使用机器学 习模型或者概率进行建模。然后根据倾向性得分估计平均因果效应,可以采用分层加权或者逆概加权。
四、回归估计
其思想是 使用机器学习模型建模给定处理Z和混杂变量Z时结果Y的期望,即 ,然后用这回归模型进行干预,即可得到平均因果效应的估计值。
,然后用这回归模型进行干预,即可得到平均因果效应的估计值。








 文章探讨了RCM(潜在结果框架)和因果图的关系,强调RCM在因果效应分析中的准确性。介绍了个体和平均因果效应的概念,以及在非随机化数据中遇到的挑战。倾向性得分和回归估计被提出作为处理混杂因素和估计平均因果效应的方法,其中倾向性得分是给定混杂变量下处理获得的概率,而回归估计则利用机器学习模型来建模结果的期望。
文章探讨了RCM(潜在结果框架)和因果图的关系,强调RCM在因果效应分析中的准确性。介绍了个体和平均因果效应的概念,以及在非随机化数据中遇到的挑战。倾向性得分和回归估计被提出作为处理混杂因素和估计平均因果效应的方法,其中倾向性得分是给定混杂变量下处理获得的概率,而回归估计则利用机器学习模型来建模结果的期望。
















 1496
1496

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








