crc 海明码

海明码原理

通过计算海明码的值修正一串二进制中的出错的位置(只能修正一位)，
若二进制串有x位，需要在其中填充k位，并满足2^k-1>=x+k
假设填充后的二进制串为x’，则k0填充在x’的第0位，并且它的值需要满足x’串第0,2,4…位亦或后的值为1.
其中0,2,4…的规律是第0位的值是0。
所以，对于一串出错的二进制串，我们可以计算其0,2,4…位的亦或和，若值为0，说明出错的位置数的第0位肯定也是0；若值为1，则说明位置数第0位为1. 位置数的其它位可以以此类推。

crc

由以上分析可知，既然除数是随机，或者按标准选定的，所以CRC校验的关键是如何求出余数，也就是校验码（CRC校验码）。

下面以一个例子来具体说明整个过程。现假设选择的CRC生成多项式为G（X） = X4 + X3 + 1，要求出二进制序列10110011的CRC校验码。下面是具体的计算过程：

（1）首先把生成多项式转换成二进制数，由G（X） = X4 + X3 + 1可以知道（，它一共是5位（总位数等于最高位的幂次加1，即4+1=5），然后根据多项式各项的含义（多项式只列出二进制值为1的位，也就是这个二进制的第4位、第3位、第0位的二进制均为1，其它位均为0）很快就可得到它的二进制比特串为11001。

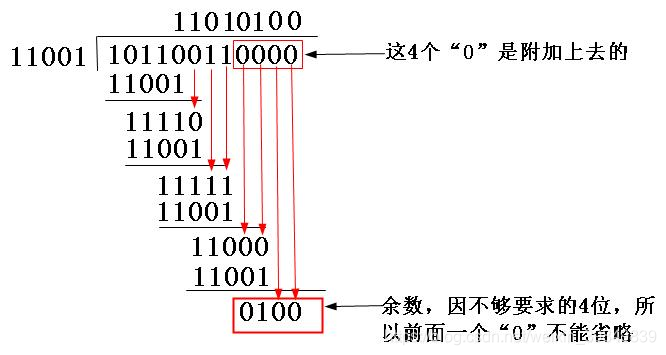
（2）因为生成多项式的位数为5，根据前面的介绍，得知CRC校验码的位数为4（校验码的位数比生成多项式的位数少1）。因为原数据帧10110011，在它后面再加4个0，得到101100110000，然后把这个数以“模2除法”方式除以生成多项式，得到的余数（即CRC码）为0100，如图5-10所示。注意参考前面介绍的“模2除法”运算法则。

图5-10 CRC校验码计算示例

（3）把上步计算得到的CRC校验0100替换原始帧101100110000