三角形一点到三边距离最小_Geogebra 制作同步课件（12）等边三角形内任意一点到三边的距离之和为定值...

点击上方蓝色文字关注我们吧~

Geogebra

同步课件系列(12)

courseware

等边三角形内任意一点到三边的距离之和为定值。(等于其高)

01-

课题说明

等边三角形内任意一点到三边的距离之和为定值。(等于其高)。这条等边三角形的性质课本里面是没有，但经过查询，这个定理是喜欢考的一个考点，让学生证明这条定理。这条定理证明还是比较简单，用面积去证就可以了。这个课件主要用动图来证明这个定理。

02-

课件制作

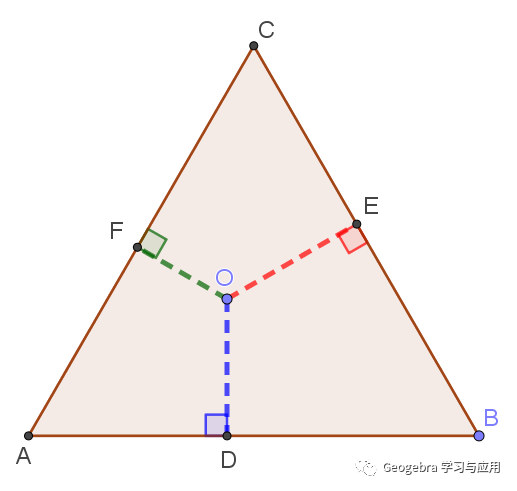
制作等边三角形，及3条垂线段。

A=交点(x轴, y轴)

B=描点(x轴)

poly1=多边形(A, B, 3)

O=内点(poly1)

i=线段(O, D)

j=线段(O, E)

k=线段(O, F)

α=角度(O, F, C)

β=角度(O, E, B)

γ=角度(O, D, A)

完成后让上图设置。最后效果如上图

创建控制线段平移旋转的滑动条a,方法如上图。将这个滑动条分解成7个滑动条。

l1=序列(如果(a < i, 0, i ≤ a < i + 1, a - i, 1), i, 0, 6)

注：这条指令相当于写了6个关于a的分段函数。

当i=0时，如果(a < 0, 0, 0 ≤ a < 0 + 1, a - 0, 1)

当i=1时，如果(a < 1, 0, 1 ≤ a < 1 + 1, a - 1, 1)

当i=2时，如果(a < 2, 0, 2 ≤ a < 2 + 1, a - 2, 1)

后面三个我不写，如果不明白自己把i带入就能得到后面三个分段函数了。

制作等边三角形高的边界

G=(x(B) + 2, y(C))

H=(x(B) + 2, y(B))

l=线段(C, 描点(线段(C, G), l1(1)))

m=线段(B, 描点(线段(B, H), l1(2)))

让三条垂线段旋转和平移起来

n=平移(线段(旋转(O, -(120°) l1(3), O), 旋转(E, -(120°) l1(3), O)), l1(4) (G - O))

p=平移(线段(旋转(O, 120° l1(5), O), 旋转(F, 120° l1(5), O)), l1(6) (G + (0, -j) - O))

i'=平移(i, l1(7) (H - D))

对点，线段的颜色，显示灯进行一下设置，设置完毕后如上图。

03-

效果展示

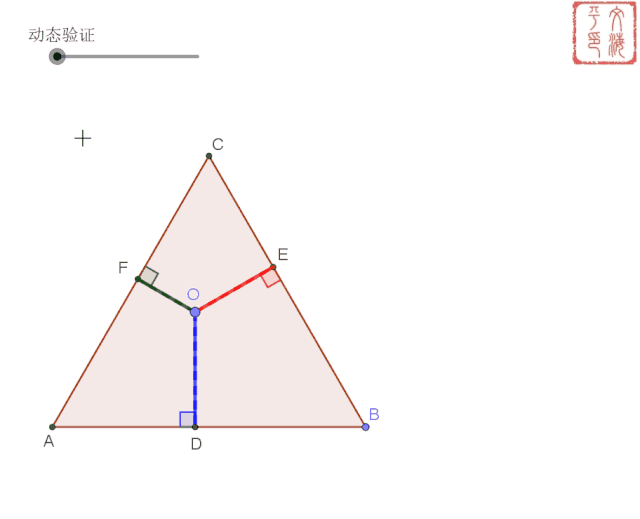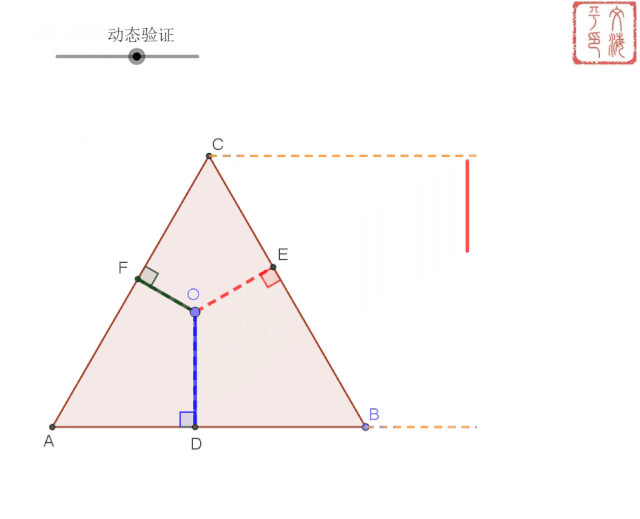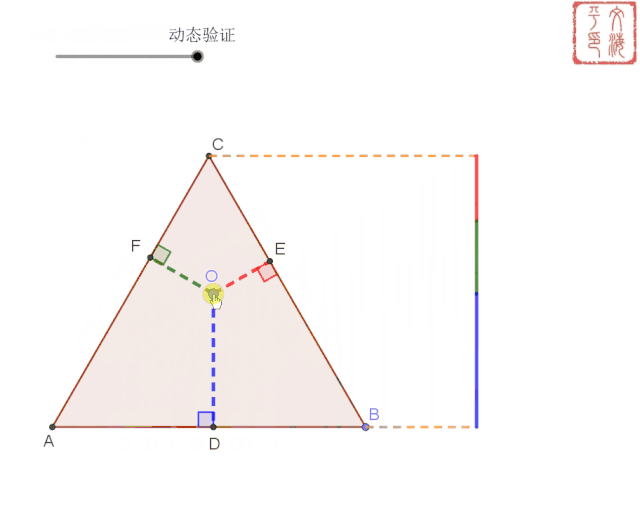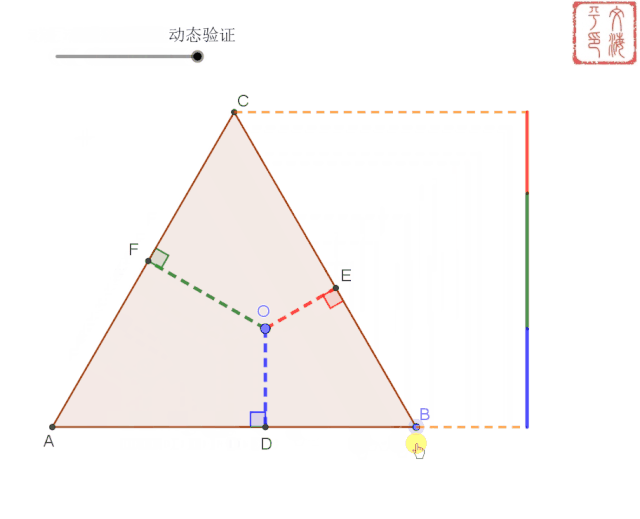
到此课件制作完成，看看效果吧。

04-

课件下载

点击文件尾部“喜欢作者”，支付任意赞赏金后会自动收到课件下载网址。

THEEND

扫码关注我

点个“在看”表示朕

已阅