集合的嵌套结果映射并分页_MP123：线性代数补习班(10)：线性映射的核与像

作为态射的线性映射

现在在线性空间范畴上讨论态射

，即线性空间之间的线性映射。回顾一下线性代数中的基本知识，有限维情况下

的矩阵表示记为

使得：

这里使用了Einstein求和约定。

的核与像定义为：

代数学中一个基本的结果是第一群同构定理(First Group Isomorphism Theorem)。在

群范畴中，令

，那么群对正规子群

做商群，满足：

现在我们在线性空间中讨论映射的核与像，仍然保有这一同构的性质，只是把群拓展为线性空间，把子群拓展为线性子空间，把商群拓展为商空间。群和线性空间的关系可以理解为

的遗忘函子。

在线性代数中花了很大篇幅讨论矩阵的秩，秩的概念在同调代数中有更加简洁的表述。由于矩阵

的秩的不同，态射

的核与像在上式中有不同的包含关系，通常我们用商空间来刻画，并将商空间定义为余像和余核：

当

时，作为

单的(injective)映射是 单射(injection)，态射称为 单同态(monomorphism)。当

时，或者等价地

，作为

满的(surjective)映射是 满射(surjection)，态射称为 满同态(epimorphism)。单满同态就是 同构(isomorphism)。

极限

现在把这些概念放到范畴论中讨论。范畴

由对象集合

和态射集合

组成。把对象作为顶点，把态射作为箭头，可以方便地用有向图对范畴进行总体或者局部的描述。若范畴中的对象​

，在图​

中满足：对于图中任意顶点对象​，存在态射

​。对于图中的任意态射​

，当然也有

​和​

。如果另有对象

​也满足以上条件，并且存在唯一的态射

，使得下图交换，那么称

构成图

​的

极限(limit)：

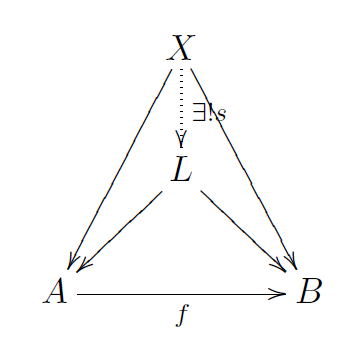
均衡子与核

下面讨论一种特殊的极限。下图的极限

称为

均衡子(equalizer)，在前面线性空间范畴的例子中，就是线性空间

的两个线性映射

和

的均衡子：

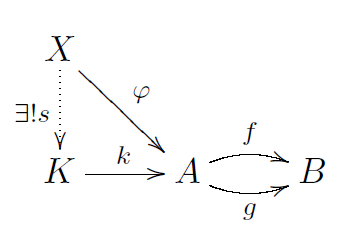
这里

​。根据定义，若有另一个

满足交换条件，则存在唯一的

使得上图交换。

回到线性空间范畴的例子，考虑

形的线性映射

。零映射

的矩阵表示为元素全零的矩阵

，根据(2)有：

根据(3)有：

如果范畴

​有零对象，且​

是零同态，那么下图中的极限​称为

核(kernel)。

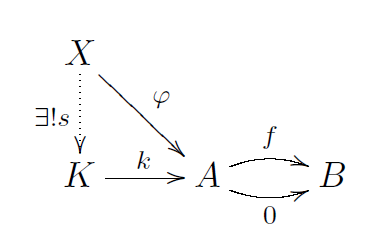
用线性代数的例子易于理解，这里

，

为恒同映射，这样便满足了均衡的条件，即对于

复合映射满足

。若有线性空间

，且它们为嵌套的线性子空间：

，显然可以构造线性映射

，且存在唯一的线性映射

，它就是自然投影映射。

余极限与余核

在极限的定义中，将箭头反向可以得到余极限(colimit)的定义。进一步，可以定义余均衡子(co-equalizer)，以及余核(cokernel)。我们把这几个概念，连同前面的概念放在一张图上：

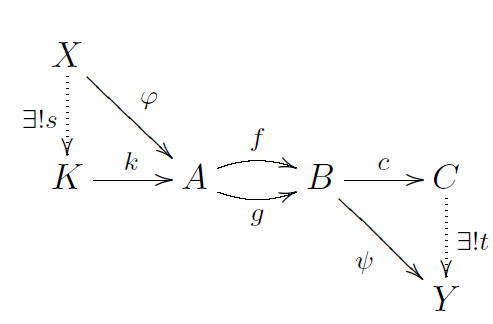
其中：

• 为
  的均衡子；
• 为
  的余均衡子；

当

为零同态时：

• 的均衡子
  为
  的核；
• 的余均衡子
  为
  的余核；