格兰杰因果检验_【视频教程】Eviews系列15|VAR模型和VEC模型之格兰杰因果检验与最优滞后阶数判断...

最新推荐文章于 2024-09-28 20:56:59 发布

weixin_39933356

最新推荐文章于 2024-09-28 20:56:59 发布

阅读量8.2k

点赞数 3

文章标签：格兰杰因果检验滞后阶数统计检验时间序列分析显著性水平

本文链接：https://blog.csdn.net/weixin_39933356/article/details/111338418

版权

点击上面 “蓝字”关注我们本期学习的内容是格兰杰因果检验与最优滞后阶数判断。实操： 1 格兰因果检验 注: 格兰杰因果检验的前提条件为:变量必须为平稳序列, 若变量不平稳,则不能进行格兰杰因果检验。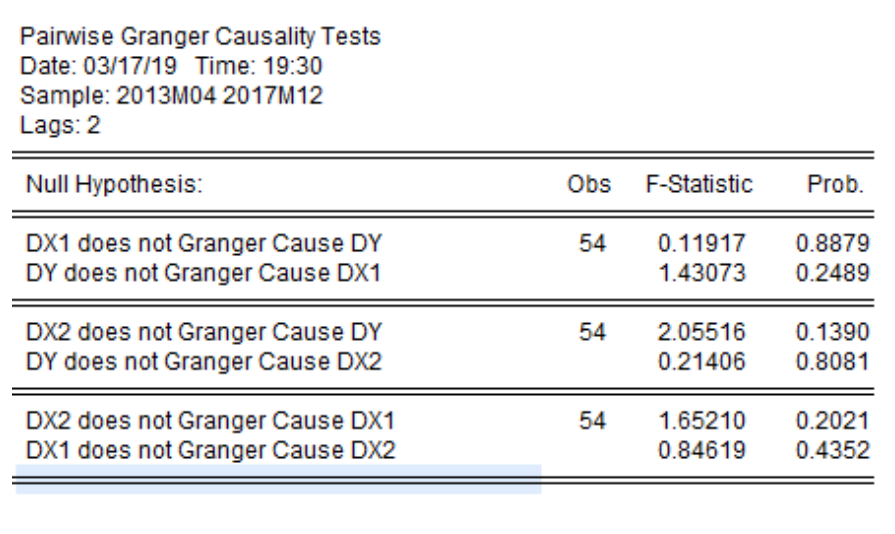

上图表格展示的三个变量的格兰杰因果检验结果从中能够看出,当原假设为“DX1不是DY的格兰杰原因”时,经过F检验对应的统计值为0.1192,相应的P值为0.8879,大于0.05,可见在5%的显著性水平下,不能拒绝原假设,即DX1不是DY的格兰杰原因；反之,当原假设为“DY不是DX1的格兰杰原因”时,经过F检验对应的统计值为0.2489,相应的P值为0.2489,大于0.05,可见在5%的显著性水平下,不能拒绝原假设,即DY不是DX1的格兰杰原因。按照同样的分析方式,我们发现,在5%的显著性水平下,DY、DX1与DX2之间并不互为因果关系。 2 最优滞后阶数判断

在进行相关检验后,我们对其进行最优滞后阶数的判断,上图展示的是5个统计量LR,FPE,AIC,SC及HQ不同滞后期的评价值。能够看出,LR显示的最优滞后阶数为滞后1阶,FPE显示的最优滞后阶数为1阶,同样,其余几个变量的最优滞后阶数为滞后1阶,由此,我们确定的最优滞后阶数为滞后1阶。 判断最优滞后阶数的原则为: (1)不同滞后阶数中,被5个评价量选中最多的滞后阶数为最优滞后阶数; (2)若有两个滞后阶数的评价量数量一样,则以AIC或SC的结果为准。

未完待续，下期见