今天为各位讲解分支定界(branch-and-bound, B&B)算法求解0-1背包问题(0-1KP),我们之前在运筹学(最优化理论)学习笔记 | 分支定界法这篇推文中讲解了分支定界算法的基本操作步骤,忘记B&B算法的小伙伴可以点击上述链接复习一下。
1.0-1背包问题描述
我们之前在遗传算法求解0-1背包问题(附matlab源代码)这篇推文中对0-1背包问题进行过描述。
实际上,0-1背包问题就是将若干个重量已知、价值已知的物品装入载重量已知的背包中,使得装进背包中物品的总价值最大。具体数学描述如下:
假设有 n n n个物品,其物品 i i i的重量用 a i ( i = 1 , 2 , . . . , n ) a_{i} (i=1,2,...,n) ai(i=1,2,...,n)表示,物品 i i i的价值用 b i ( i = 1 , 2 , . . . , n ) b_{i} (i=1,2,...,n) bi(i=1,2,...,n)表示,背包的最大载重量为 c c c,如果物品i被装入背包,则 x i = 1 x_{i}=1 xi=1,否则 x i = 0 x_{i}=0 xi=0。
2.数学模型
根据上述描述,0-1KP问题的整数规划模型如下:
max
∑
i
=
1
n
c
i
x
i
s.t.
∑
i
=
1
n
a
i
x
i
≤
b
x
i
∈
{
0
,
1
}
\begin{array}{ll} \max & \sum_{i=1}^{n} c_{i} x_{i} \\ \text { s.t. } \quad & \sum_{i=1}^{n} a_{i} x_{i} \leq b \\ & x_{i} \in\{0,1\} \end{array}
max s.t. ∑i=1ncixi∑i=1naixi≤bxi∈{0,1}
其中
c
i
>
0
,
a
i
>
0
,
i
=
1
,
.
.
.
,
n
c_{i}>0,a_{i}>0,i=1,...,n
ci>0,ai>0,i=1,...,n。现在对上述整数规划模型进行松弛,即变量
x
i
x_{i}
xi的取值不仅仅为0或1,而变为0~1之间的任何数,则0-1KP问题的线性规划松弛模型如下:
max
∑
i
=
1
n
c
i
x
i
s.t.
∑
i
=
1
n
a
i
x
i
≤
b
x
i
∈
[
0
,
1
]
\begin{array}{ll} \max & \sum_{i=1}^{n} c_{i} x_{i} \\ \text { s.t. } \quad & \sum_{i=1}^{n} a_{i} x_{i} \leq b \\ & x_{i} \in[0,1] \end{array}
max s.t. ∑i=1ncixi∑i=1naixi≤bxi∈[0,1]
3.线性规划松弛最优解
一般来说求解线性规划松弛问题常采用的办法为单纯形法,但是由于背包问题约束的特殊性,实际上可以采用贪婪法求解上述线性规划松弛模型,而不必用单纯形法。
贪婪法的基本思想是尽可能将性价比高的物品装入背包,那么性价比的含义是什么?
物
品
i
的
性
价
比
=
物
品
i
的
价
值
物
品
i
的
重
量
=
c
i
a
i
物品i的性价比=\frac{物品i的价值}{物品i的重量}=\frac{c_{i}}{a_{i}} \\
物品i的性价比=物品i的重量物品i的价值=aici
先将物品按照性价比
{
c
i
a
i
}
\left\{\frac{c_{i}}{a_{i}}\right\}
{aici}进行降序排列,假设排序结果如下:
c
1
a
1
≥
c
2
a
2
≥
.
.
.
≥
c
n
a
n
\frac{c_{1}}{a_{1}} \geq \frac{c_{2}}{a_{2}} \geq ... \geq \frac{c_{n}}{a_{n}}
a1c1≥a2c2≥...≥ancn
设
s
s
s是使下式成立的最大指标
k
k
k:
∑
j
=
1
k
a
j
≤
b
\sum_{j=1}^{k}{a_{j}} \leq b
j=1∑kaj≤b
该式的含义为:根据排序结果最多将性价比最高的前
s
s
s个物品装进背包,刚好不会超出背包载重量。一旦将性价比排在第
s
+
1
s+1
s+1位的物品也装入背包,则会超出背包载重量。
综上所述,0-1KP问题线性规划松弛模型的最优解为
x
j
=
1
,
j
=
1
,
…
,
s
x
j
=
0
,
j
=
s
+
2
,
…
,
n
x
s
+
1
=
(
b
−
∑
j
=
1
k
a
j
)
/
a
s
+
1
\begin{gathered} x_{j}=1, \quad j=1, \ldots, s \\ x_{j}=0, \quad j=s+2, \ldots, n \\ x_{s+1}=\left(b-\sum_{j=1}^{k} a_{j}\right) / a_{s+1} \end{gathered}
xj=1,j=1,…,sxj=0,j=s+2,…,nxs+1=(b−j=1∑kaj)/as+1
最优解的实际含义如下:
x j = 1 , j = 1 , . . . , s x_{j}=1, \quad j=1,...,s xj=1,j=1,...,s表示将性价比最高的前 s s s个物品装进背包。
x j = 0 , j = s + 2 , . . . , n x_{j}=0, \quad j=s+2,...,n xj=0,j=s+2,...,n表示性价比排在第 s + 2 s+2 s+2位以后的物品都不会装包。
x s + 1 = ( b − ∑ j = 1 k a j ) / a s + 1 x_{s+1}=(b-\sum_{j=1}^{k}{a_{j}})/a_{s+1} xs+1=(b−∑j=1kaj)/as+1表示性价比排在第 s + 1 s+1 s+1位的物品只会将其一部分装进背包,使背包内物品的总质量刚好达到背包载重量。
4.实例讲解
现有5个物品,每个物品的重量分别为
[
12
,
7
,
11
,
8
,
9
]
[12,7,11,8,9]
[12,7,11,8,9],价值分别为
[
24
,
13
,
23
,
15
,
16
]
[24,13,23,15,16]
[24,13,23,15,16],背包载重量为26,则就上述数据构建的整数规划数学模型如下:
max
24
x
1
+
13
x
2
+
23
x
3
+
15
x
4
+
16
x
5
s.t.
12
x
1
+
7
x
2
+
11
x
3
+
8
x
4
+
9
x
5
≤
26
x
1
,
x
2
,
x
3
,
x
4
,
x
5
∈
{
0
,
1
}
\begin{array}{cl} \max & 24 x_{1}+13 x_{2}+23 x_{3}+15 x_{4}+16 x_{5} \\ \text { s.t. } & 12 x_{1}+7 x_{2}+11 x_{3}+8 x_{4}+9 x_{5} \leq 26 \\ & x_{1}, x_{2}, x_{3}, x_{4}, x_{5} \in\{0,1\} \end{array}
max s.t. 24x1+13x2+23x3+15x4+16x512x1+7x2+11x3+8x4+9x5≤26x1,x2,x3,x4,x5∈{0,1}
根据第3节线性规划松弛最优解,对上述物品按照性价比进行排序,排序结果如下:
23
11
≥
24
12
≥
15
8
≥
13
7
≥
16
9
\frac{23}{11} \geq \frac{24}{12} \geq \frac{15}{8} \geq \frac{13}{7} \geq \frac{16}{9}
1123≥1224≥815≥713≥916
即
c
3
a
3
≥
c
1
a
1
≥
c
4
a
4
≥
c
2
a
2
≥
c
5
a
5
\frac{c_{3}}{a_{3}} \geq \frac{c_{1}}{a_{1}} \geq \frac{c_{4}}{a_{4}} \geq \frac{c_{2}}{a_{2}} \geq \frac{c_{5}}{a_{5}}
a3c3≥a1c1≥a4c4≥a2c2≥a5c5
此时可以将物品3和物品1装入背包中,且没有超出背包载重量,即
a
3
+
a
1
≤
b
11
+
12
≤
26
\begin{gathered} a_{3}+a_{1} \leq b \\ 11 + 12 \leq 26 \end{gathered}
a3+a1≤b11+12≤26
因此,最优解如下:
x
3
=
1
,
x
1
=
1
x
2
=
0
,
x
5
=
0
x
4
=
(
26
−
11
−
12
)
/
8
=
0.375
\begin{gathered} x_{3}=1, \quad x_{1}=1 \\ x_{2}=0, \quad x_{5}=0 \\ x_{4}=(26-11-12) / 8=0.375 \end{gathered}
x3=1,x1=1x2=0,x5=0x4=(26−11−12)/8=0.375
综上所述,该问题的线性规划松弛的最优解为
(
1
,
0
,
1
,
0.375
,
0
)
(1,0,1,0.375,0)
(1,0,1,0.375,0),对应的上界为52.625。此节点编号为0,节点深度为1。
在分支定界过程中,在剪支后如何从搜索树中剩下的节点(子问题)中选择一个节点继续进行分支也将影响整个分支定界的收敛速度,本文我们将使用深度优先策略。
深度优先含义如下:把分支定界树的层数定义为节点的深度,深度优先策略是选择具有最大深度的节点进行分支,从而快速找到可行解。
选择分数变量
x
4
x_{4}
x4进行分支,固定
x
4
=
0
x_{4}=0
x4=0和
x
4
=
1
x_{4}=1
x4=1,则得到2个子问题:
(
P
1
)
max
24
x
1
+
13
x
2
+
23
x
3
+
16
x
5
s.t.
12
x
1
+
7
x
2
+
11
x
3
+
9
x
5
≤
26
(
P
2
)
max
24
x
1
+
13
x
2
+
23
x
3
+
15
+
16
x
5
s.t.
12
x
1
+
7
x
2
+
11
x
3
+
8
+
9
x
5
≤
26
x
1
,
x
2
,
x
3
,
x
5
∈
{
0
,
1
}
\begin{array}{c} (P 1) \max \quad 24 x_{1}+13 x_{2}+23 x_{3}+16 x_{5} \\ \text { s.t. } \quad 12 x_{1}+7 x_{2}+11 x_{3}+9 x_{5} \leq 26 \\ (P 2) \max \quad 24 x_{1}+13 x_{2}+23 x_{3}+15+16 x_{5} \\ \text { s.t. } \quad 12 x_{1}+7 x_{2}+11 x_{3}+8+9 x_{5} \leq 26 \\ x_{1}, x_{2}, x_{3}, x_{5} \in\{0,1\} \end{array}
(P1)max24x1+13x2+23x3+16x5 s.t. 12x1+7x2+11x3+9x5≤26(P2)max24x1+13x2+23x3+15+16x5 s.t. 12x1+7x2+11x3+8+9x5≤26x1,x2,x3,x5∈{0,1}
子问题(P1)的线性规划松弛的最优解为
(
1
,
0.43
,
1
,
0
)
(1,0.43,1,0)
(1,0.43,1,0),对应的上界为52.57**,此节点编号为1,节点深度为2**。子问题(P2)的线性规划松弛的最优解为
(
0.58
,
0
,
1
,
0
)
(0.58,0,1,0)
(0.58,0,1,0),对应的上界为52,此节点编号为2,节点深度为2。分支过程如下图所示:
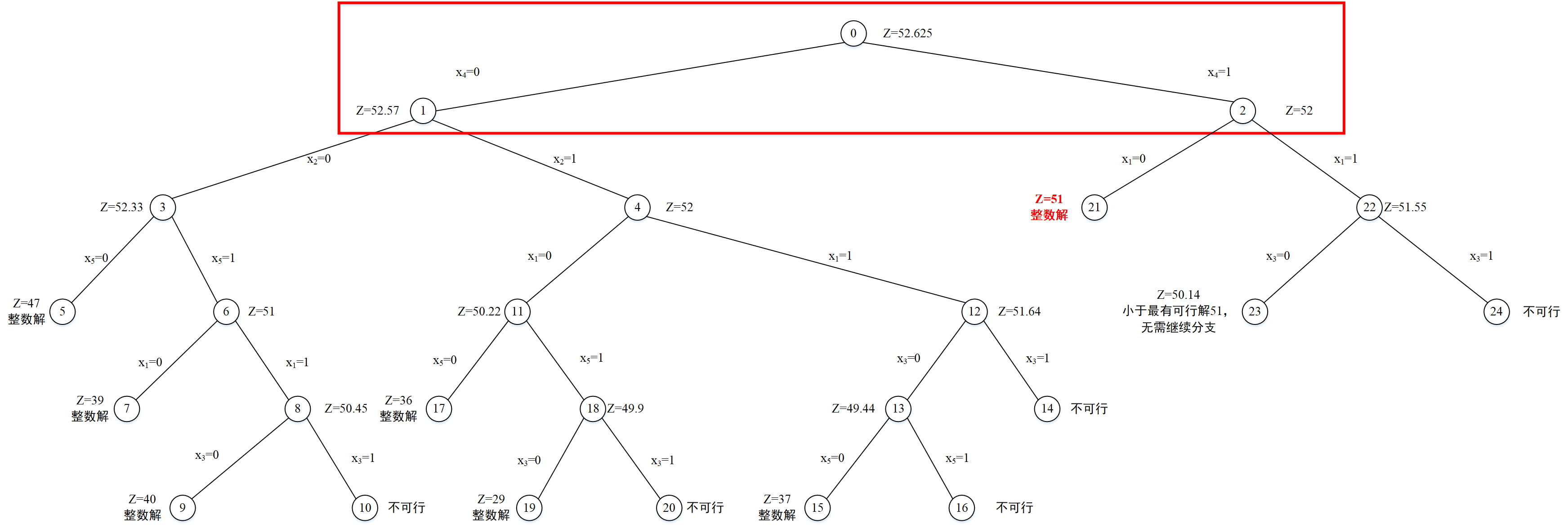
选择子问题(P1),选择分数变量
x
2
x_{2}
x2进行分支,固定
x
2
=
0
x_{2}=0
x2=0和
x
2
=
1
x_{2}=1
x2=1,则得到2个子问题:
$$
\begin{array}{c}
(P1)\quad max \quad 24x_{1}+23x_{3}+16x_{5} \
s.t. \quad 12x_{1}+11x_{3}+9x_{5}\leq 26 \
x_{1},x_{3},x_{5} \in \left{ 0,1\right} \
(P2)\quad max \quad 24x_{1}+13+23x_{3}+16x_{5} \
s.t. \quad 12x_{1}+7+11x_{3}+9x_{5}\leq 26 \
x_{1},x_{3},x_{5} \in \left{ 0,1\right} \
\end{array}
$$
子问题(P1)的线性规划松弛的最优解为
(
1
,
1
,
0.33
)
(1,1,0.33)
(1,1,0.33),对应的上界为52.33**,此节点编号为3,节点深度为3**。子问题(P2)的线性规划松弛的最优解为
(
0.67
,
1
,
0
)
(0.67,1,0)
(0.67,1,0),对应的上界为52**,此节点编号为4,节点深度为3**。分支过程如下图所示:

选择子问题(P1),选择分数变量
x
5
x_{5}
x5进行分支,固定
x
5
=
0
x_{5}=0
x5=0和
x
5
=
1
x_{5}=1
x5=1,则得到2个子问题:
$$
\begin{array}{c}
(P1)\quad max \quad 24x_{1}+23x_{3} \
\quad\quad\quad s.t. \quad 12x_{1}+11x_{3}\leq 26 \
\quad \quad \quad x_{1},x_{3} \in \left{ 0,1\right} \quad \
(P2)\quad max \quad 24x_{1}+23x_{3}+16 \
\quad\quad\quad s.t. \quad 12x_{1}+11x_{3}+9\leq 26 \
\quad \quad \quad x_{1},x_{3} \in \left{ 0,1\right} \quad \
\end{array}
$$
子问题(P1)的线性规划松弛的最优解为
(
1
,
1
)
(1,1)
(1,1),对应的上界为47,此节点编号为5,节点深度为4,因为此节点最优解为整数解,所以先保留此整数解作为当前最优可行解,不需要继续对该节点进行分支。子问题(P2)的线性规划松弛的最优解为
(
0.5
,
1
)
(0.5,1)
(0.5,1),对应的上界为51,此节点编号为6,节点深度为4。分支过程如下图所示:

选择子问题(P2),选择分数变量
x
1
x_{1}
x1进行分支,固定
x
1
=
0
x_{1}=0
x1=0和
x
1
=
1
x_{1}=1
x1=1,则得到2个子问题:
$$
\begin{array}{c}
(P1)\quad max \quad 23x_{3}+16 \
\quad\quad\quad s.t. \quad 11x_{3}+9\leq 26 \
\quad \quad \quad x_{3} \in \left{ 0,1\right} \quad \
(P2)\quad max \quad 24+23x_{3}+16 \
\quad\quad\quad s.t. \quad 12+11x_{3}+9\leq 26 \
\quad \quad \quad x_{3} \in \left{ 0,1\right} \quad \
\end{array}
$$
子问题(P1)的线性规划松弛的最优解为
(
1
)
(1)
(1),对应的上界为39,此节点编号为7,节点深度为5,虽然此节点最优解为整数解,但是此节点解的目标函数值小于47,所以不需要继续对该节点进行分支。子问题(P2)的线性规划松弛的最优解为
(
0.45
)
(0.45)
(0.45),对应的上界为50.45,此节点编号为8,节点深度为5。分支过程如下图所示:

选择子问题(P2),选择分数变量
x
3
x_{3}
x3进行分支,固定
x
3
=
0
x_{3}=0
x3=0和
x
3
=
1
x_{3}=1
x3=1,则得到2个子问题:
$$
\begin{array}{c}
(P1)\quad max \quad 24+16 \
\quad\quad\quad s.t. \quad 12+9\leq 26 \
(P2)\quad max \quad 24+23+16 \
\quad\quad\quad s.t. \quad 12+11+9\leq 26 \
\end{array}
$$
当
x
3
=
0
x_{3}=0
x3=0时,对应的上界为40,此节点编号为9,节点深度为6,虽然此节点最优解为整数解,但是此节点解的目标函数值小于47,因此无法作为当前最优可行解。当
x
3
=
1
x_{3}=1
x3=1时,不存在可行解,此节点编号为10,节点深度为6。分支过程如下图所示:

找出当前未分支过,且节点深度最深的节点,从分支定界树中可以找出节点4为满足上述要求的节点。因此,对节点4进行分支,选择分数变量
x
1
x_{1}
x1进行分支,固定
x
1
=
0
x_{1}=0
x1=0和
x
1
=
1
x_{1}=1
x1=1,则得到2个子问题:
$$
\begin{array}{c}
(P1)\quad max \quad 13+23x_{3}+16x_{5} \
\quad\quad\quad s.t. \quad 7+11x_{3}+9x_{5}\leq 26 \
\quad \quad \quad x_{3},x_{5} \in \left{ 0,1\right} \quad
\
(P2)\quad max \quad 24+13+23x_{3}+16x_{5} \
\quad\quad\quad s.t. \quad 12+7+11x_{3}+9x_{5}\leq 26 \
\quad \quad \quad x_{3},x_{5} \in \left{ 0,1\right} \quad \
\end{array}
$$
子问题(P1)的线性规划松弛的最优解为
(
1
,
0.89
)
(1,0.89)
(1,0.89),对应的上界为50.22,此节点编号为11,节点深度为4。子问题(P2)的线性规划松弛的最优解为
(
0.64
,
0
)
(0.64,0)
(0.64,0),对应的上界为51.64,此节点编号为12,节点深度为4。分支过程如下图所示:

选择子问题(P2),选择分数变量
x
3
x_{3}
x3进行分支,固定
x
3
=
0
x_{3}=0
x3=0和
x
3
=
1
x_{3}=1
x3=1,则得到2个子问题:
$$
\begin{array}{c}
(P1)\quad max \quad 24+13+16x_{5} \
\quad\quad\quad s.t. \quad 12+7+9x_{5}\leq 26 \
\quad \quad \quad x_{5} \in \left{ 0,1\right} \quad \
(P2)\quad max \quad 24+13+23+16x_{5} \
\quad\quad\quad s.t. \quad 12+7+11+9x_{5}\leq 26 \
\quad \quad \quad x_{5} \in \left{ 0,1\right} \quad \
\end{array}
$$
子问题(P1)的线性规划松弛的最优解为
(
0.78
)
(0.78)
(0.78),对应的上界为49.44,此节点编号为13,节点深度为5。子问题(P2)不存在可行解,此节点编号为14,节点深度为5。分支过程如下图所示:

选择子问题(P1),选择分数变量
x
5
x_{5}
x5进行分支,固定
x
5
=
0
x_{5}=0
x5=0和
x
5
=
1
x_{5}=1
x5=1,则得到2个子问题:
$$
\begin{array}{c}
(P1)\quad max \quad 24+13 \
\quad\quad\quad s.t. \quad 12+7\leq 26 \
(P2)\quad max \quad 24+13+16 \
\quad\quad\quad s.t. \quad 12+7+9\leq 26 \
\end{array}
$$
当
x
5
=
0
x_{5}=0
x5=0时,对应的上界为37,此节点编号为15,节点深度为6,虽然此节点最优解为整数解,但是此节点解的目标函数值小于47,因此无法作为当前最优可行解。当
x
5
=
1
x_{5}=1
x5=1时,不存在可行解,此节点编号为16,节点深度为6。分支过程如下图所示:
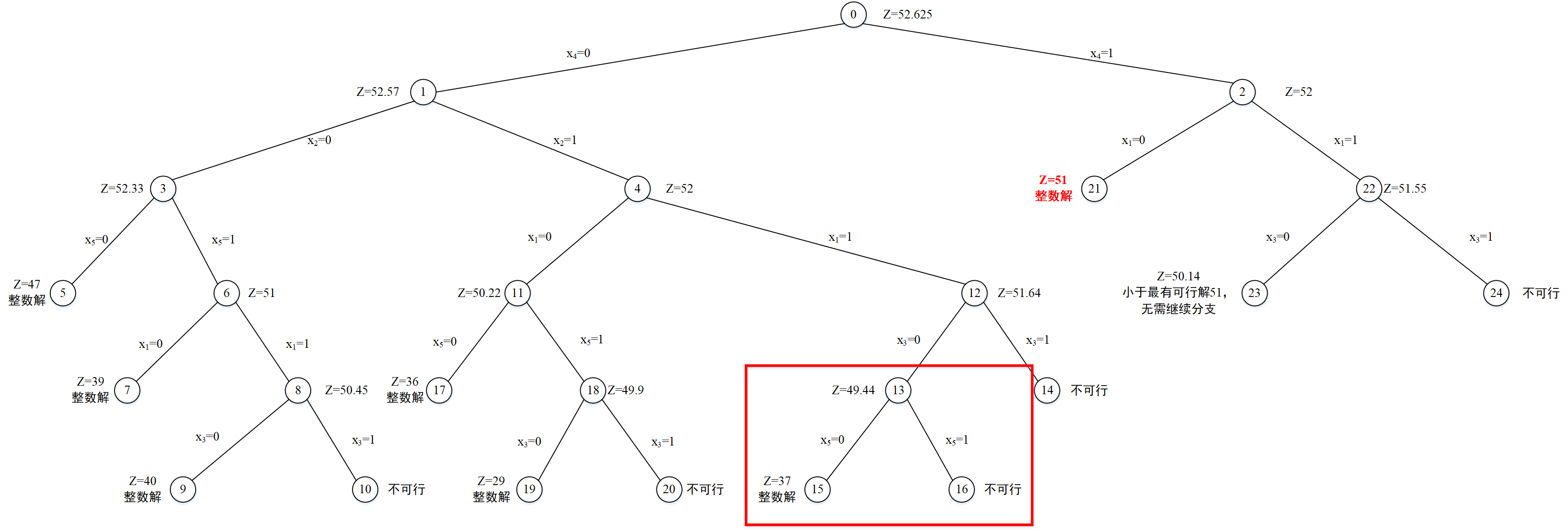
找出当前未分支过,且节点深度最深的节点,从分支定界树中可以找出节点11为满足上述要求的节点。因此,对节点11进行分支,选择分数变量
x
5
x_{5}
x5进行分支,固定
x
5
=
0
x_{5}=0
x5=0和
x
5
=
1
x_{5}=1
x5=1,则得到2个子问题:
$$
\begin{array}{c}
(P1)\quad max \quad 13+23x_{3} \
\quad\quad\quad s.t. \quad 7+11x_{3}\leq 26 \
\quad \quad \quad x_{3} \in \left{ 0,1\right} \quad \
(P2)\quad max \quad 13+23x_{3}+16 \
\quad\quad\quad s.t. \quad 7+11x_{3}+9\leq 26 \
\quad \quad \quad x_{3} \in \left{ 0,1\right} \quad \
\end{array}
$$
子问题(P1)的线性规划松弛的最优解为
(
1
)
(1)
(1),对应的上界为36,此节点编号为17,节点深度为5,虽然此节点最优解为整数解,但是此节点解的目标函数值小于47,因此无法作为当前最优可行解。子问题(P2)的线性规划松弛的最优解为
(
0.91
)
(0.91)
(0.91),对应的上界为49.9,此节点编号为18,节点深度为5。分支过程如下图所示:
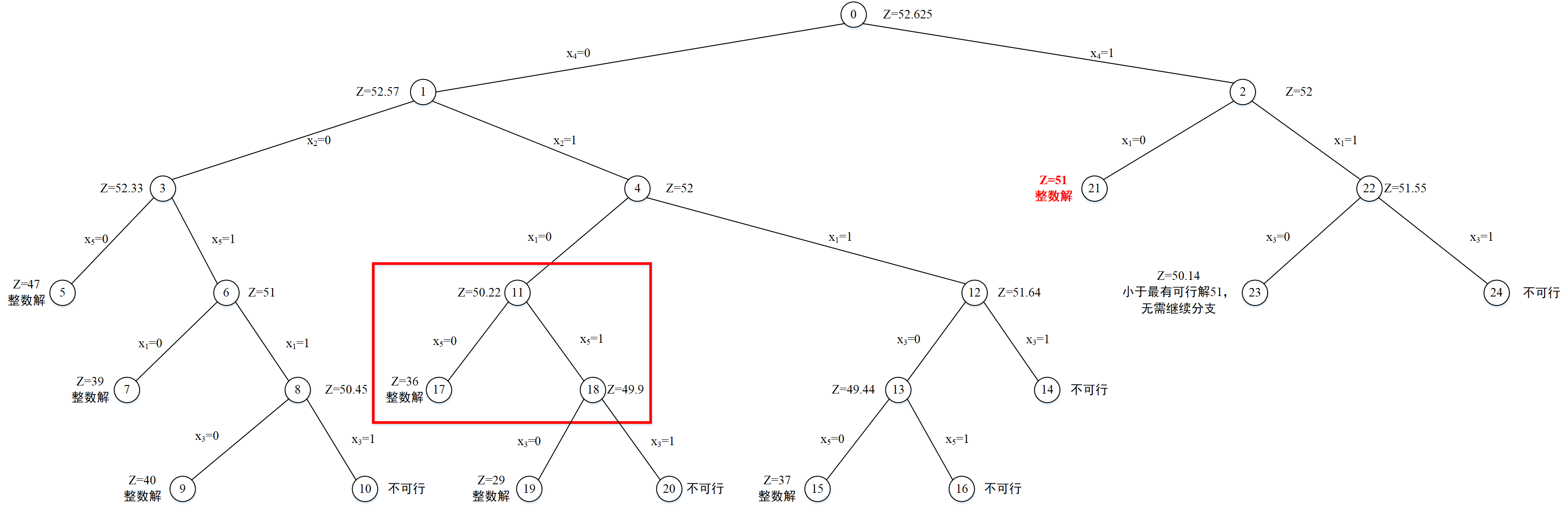
选择子问题(P2),选择分数变量
x
3
x_{3}
x3进行分支,固定
x
3
=
0
x_{3}=0
x3=0和
x
3
=
1
x_{3}=1
x3=1,则得到2个子问题:
$$
\begin{array}{c}
(P1)\quad max \quad 13+16 \
\quad\quad\quad s.t. \quad 7+9\leq 26 \
(P2)\quad max \quad 13+23+16 \
\quad\quad\quad s.t. \quad 7+11+9\leq 26 \
\end{array}
$$
当
x
3
=
0
x_{3}=0
x3=0时,对应的上界为29,此节点编号为19,节点深度为6,虽然此节点最优解为整数解,但是此节点解的目标函数值小于47,因此无法作为当前最优可行解。当
x
3
=
1
x_{3}=1
x3=1时,不存在可行解,此节点编号为20,节点深度为6。分支过程如下图所示:
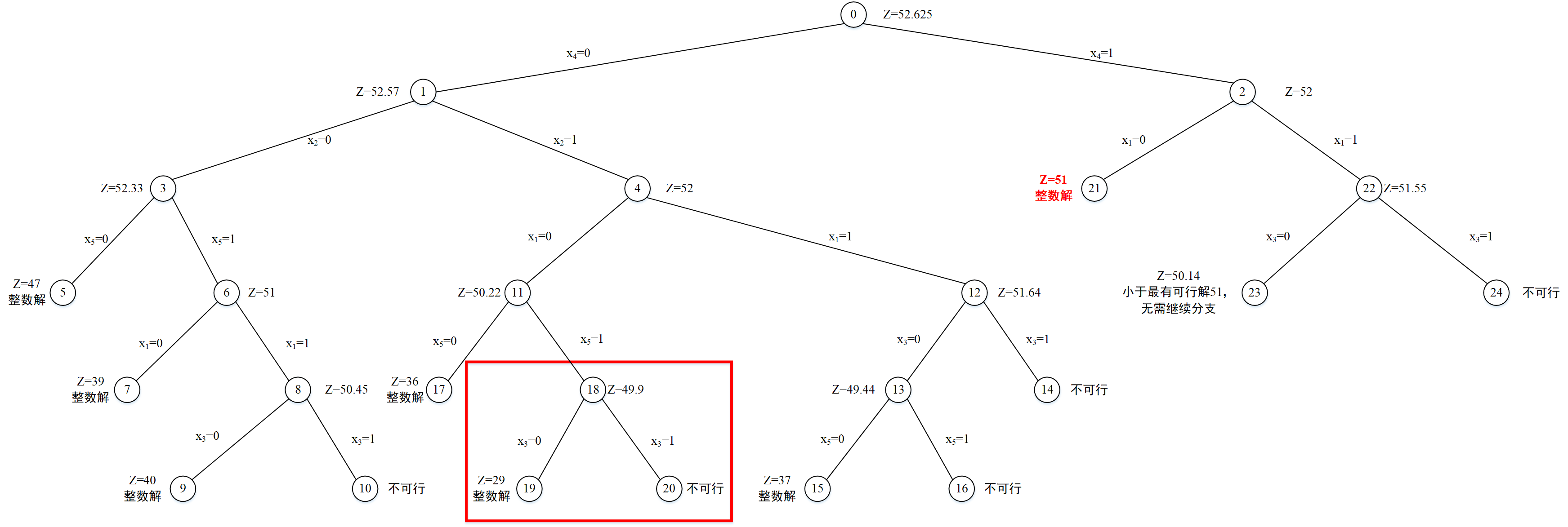
找出当前未分支过,且节点深度最深的节点,从分支定界树中可以找出节点2为满足上述要求的节点。因此,对节点11进行分支,选择分数变量
x
1
x_{1}
x1进行分支,固定
x
1
=
0
x_{1}=0
x1=0和
x
1
=
1
x_{1}=1
x1=1,则得到2个子问题:
$$
\begin{array}{c}
\quad\quad(P1)\quad max \quad 13x_{2}+23x_{3}+15+16x_{5} \
\quad\quad\quad\quad\quad s.t. \quad 7x_{2}+11x_{3}+8+9x_{5}\leq 26 \
\quad \quad \quad x_{2},x_{3},x_{5} \in \left{ 0,1\right} \quad \
\quad\quad(P2)\quad max \quad 24+13x_{2}+23x_{3}+15+16x_{5} \
\quad\quad\quad\quad\quad s.t. \quad 12+7x_{2}+11x_{3}+8+9x_{5}\leq 26 \
\quad \quad \quad x_{2},x_{3},x_{5} \in \left{ 0,1\right} \quad \
\end{array}
$$
子问题(P1)的线性规划松弛的最优解为
(
1
,
1
,
0
)
(1,1,0)
(1,1,0),对应的**上界为51,此节点编号为21,节点深度为3,因为此节点最优解为整数解**,并且此节点解的目标函数值大于47,所以**更新当前最优可行解**,且无需继续对该节点进行分支。子问题(P2)的线性规划松弛的最优解为
(
0
,
0.55
,
0
)
(0,0.55,0)
(0,0.55,0),对应的上界为51.55,此节点编号为22,节点深度为3。分支过程如下图所示:

选择子问题(P2),选择分数变量
x
3
x_{3}
x3进行分支,固定
x
3
=
0
x_{3}=0
x3=0和
x
3
=
1
x_{3}=1
x3=1,则得到2个子问题:
$$
\begin{array}{c}
\quad\quad(P1)\quad max \quad 24+13x_{2}+15+16x_{5} \
\quad\quad\quad\quad\quad s.t. \quad 12+7x_{2}+8+9x_{5}\leq 26 \
\quad \quad \quad x_{2},x_{5} \in \left{ 0,1\right} \quad \
\quad\quad(P2)\quad max \quad 24+13x_{2}+23+15+16x_{5} \
\quad\quad\quad\quad\quad s.t. \quad 12+7x_{2}+11+8+9x_{5}\leq 26 \
\quad \quad \quad x_{2},x_{5} \in \left{ 0,1\right} \quad
\end{array}
$$
子问题(P1)的线性规划松弛的最优解为
(
0.86
,
0
)
(0.86,0)
(0.86,0),对应的上界为50.14,此节点编号为23,节点深度为4,虽然此节点最优解为不是整数解,但是此节点解的目标函数值小于51,因此无需继续对该节点进行分支。子问题(P2)不存在可行解,此节点编号为24,节点深度为4。分支过程如下图所示:
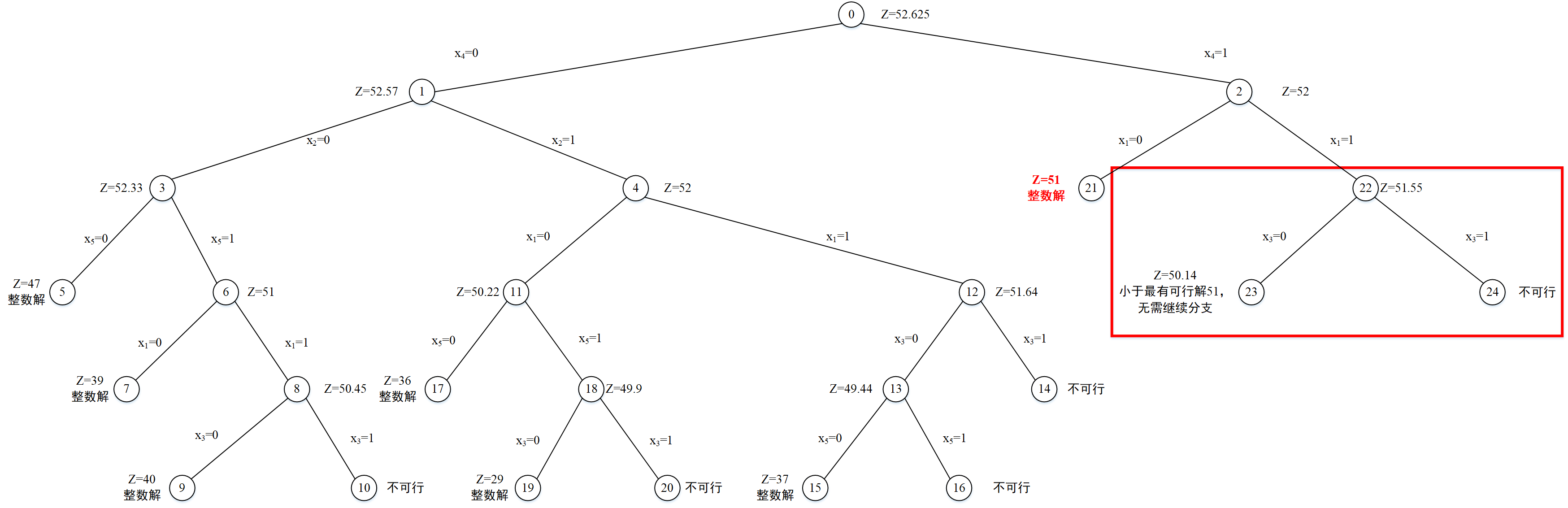
至此,最优解为[0,1,1,10],总价值为51,总重量为26,满足背包载重量约束。
5.MATLAB代码
本次推文暂时只公布MATLAB加密代码,后续如果各位有需要,我们会单独出一期推文讲解本次推文代码。
代码获取方式:公众号后台回复【BAB求解01KP】,即可获取代码。
代码使用方式如下:
%% @copyright
%微信公众号:优化算法交流地
clear
clc
tic
%% 输入数据 方式1
w=importdata('p08_w.txt')'; %物品重量
p=importdata('p08_p.txt')'; %物品价值
cap=importdata('p08_c.txt'); %背包载重量
s=importdata('p08_s.txt'); %已知最优解
%% 输入数据 方式2
% p=[8,11,6,4];
% w=[5,7,4,3];
% cap=14;
%% bnb_01kp函数
%输入w:物品重量
%输入p:物品价值
%输入cap:背包载重量
%输出bestSol:最优解,即哪些物品装包,哪些物品不装包
%输出bestValue:最优解总价值
%输出bestWeight:最优解总重量
[bestSol,bestValue,bestWeight]=bnb_01kp(w,p,cap);
toc
%微信公众号:优化算法交流地
直接在主函数main中输入数据即可,第一种输入方式:将数据存放在txt文件中,第二种输入方式:直接在代码中手动输入即可。
样例数据为:背包载重量为6404180,物品数目为24,各个物品重量和价值数据如下:
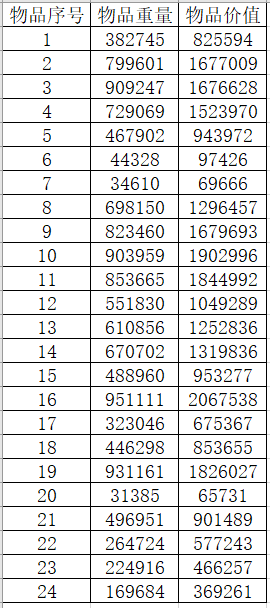
求解结果如下:

参考文献
[1] 孙小玲,李端,整数规划,科学出版社,2010
OK,今天就到这里啦,各位可点击下方图片留言。
我们已经推出粉丝QQ交流群,各位小伙伴赶快加入吧!!!

咱们下期再见
近期你可能错过了的好文章
新书上架 | 《MATLAB智能优化算法:从写代码到算法思想》
遗传算法(GA)求解带时间窗的车辆路径(VRPTW)问题MATLAB代码
粒子群优化算法(PSO)求解带时间窗的车辆路径问题(VRPTW)MATLAB代码
知乎 | bilibili | CSDN:随心390
微信公众号:优化算法交流地





















 292
292











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








