最小二乘法再次理解+python代码

Brief

此程序不通用，属于个人学习记录。前面的推导是可以看的。
 今天算是被自己蠢到了，最小二乘法给理解出了很大的问题，结果导致对问题没有很想清楚。我们知道一般最小二乘法是拟合多项式函数的。也就是对形如：
$$y=a_k^k+a_{k-1}^{k-1}+...+a_1^{}+a_0$$的函数。然后我们假设$Y_i$是测量值，$\overline{Y_i}$是拟合函数当$x=x_i$时的函数值，那么 我们的目标就是对于全局的测量数据$(X,Y)$,我们要使得每一个测量点的$Y$值和预测出的$\overline{Y}$的差的平方和最小，也就是拟合点到对应的测量数据的距离和最小，即是下面这个函数：
$$Min\sum _{i=1}^n(Y_i-\overline{Y_i}{)}^2$$这里面的$n$表示测量的样本个数。

问题描述

 收到的数据含有一个固定的公式，如下：
$$F_N=\frac{4\times {R^{\ast }}^{\frac{1}{2}}\times E^{\ast }\times {\delta }_n^{\frac{3}{2}}}{3}$$
其中的$R^{\ast }$为一个常数值，${\delta }_n和F_N$是实验测试出来的数据，我们的目标就是采用一种拟合的方式求解这个参数$E^{\ast }$,所以整合一下数据，这其实也就是一个正比例函数关系，拟合一个正比例的系数就可了。如下：
$$\begin{gathered} 令：x=\frac{4\times {R^{\ast }}^{\frac{1}{2}}\times {\delta }_n^{\frac{3}{2}}}{3} \\ y=F_N \\ then: \\ y=E^{\ast }x \end{gathered}$$

问题解决

最开始这里的理解出现了比较大的问题。因为以前求解一次关系的函数：
$$y=kx+b$$
都是通过单个算式的方式，而不是直接用矩阵的方式去求解，采取算法的方式即是：
$$\begin{gathered} k=\frac{{\sum }_1^n{x}_i{y}_i-n\times \overline{x}\times \overline{y}}{{\sum }_1^n{x}_i^2-n\times {\overline{x}}^2} \\ b=\overline{y}-w\times \overline{x} \end{gathered}$$
然后看着公式我就陷入了深深的疑惑，我这个函数没有$b$呀！也就是说我要过定点$(0,0)$去拟合这这个参数$E^{\ast }$,好吧。那也没关系，我可以求一个斜率的范围，然后通过程序暴力遍历也可以找到一个大致的值，好的，准备动手，emmm。先画一张图来看看y和新的x之间的关系吧，如下：

好的，看到这么大一个的数字，这个暴力遍历的方法算是破灭了。于是我又开始了我的疑惑，按照上诉的y=kx+b的回归方程，我传进去数据肯定会得到两个参数，一个k，一个b,我要如何才能只得到k而没有b呢。所以就是这么一个思想让我觉得这不是一个一般的拟合。其实是我对其中的内在求解没有理解。
回到最开始的问题：我们在优化测量值和拟合函数值的平方和。怎么做的这个过程？实际上是先建立目标函数：
$$Min\sum _{i=1}^n(y_i-(k{x}_i+b){)}^2$$
目标函数分别对参数$k和参数b$求导就得到了对应的更新公式。尽管在最后k的表达式和b无关，也就是：
$$\begin{gathered} k=\frac{{\sum }_1^n{x}_i{y}_i-n\times \overline{x}\times \overline{y}}{{\sum }_1^n{x}_i^2-n\times {\overline{x}}^2} \\ b=\overline{y}-w\times \overline{x} \end{gathered}$$
这是因为目标函数对b求导是：
$$b=\overline{y}-w\times \overline{x}$$带回了原来的式子中，导致了这么一个结果。如果我需要b=0；就是相当于多加了一个约束调价而已。没有什么差别。哎。头秃！被自己蠢哭了。

后续解决

既然是一样的，那就开始解决吧，这里先给多项式的拟合形式，就会觉得采用矩阵运算比上面的公式简单过来。
考虑超定方程组（超定指未知数小于方程个数）：
$$\sum {j=1}^n{X}_{ij}{\beta }_{ij}=y_i,(i=1,2,3,...m)$$
其中m代表有m个等式，n代表有 n 个未知数$\beta$ ，m>n ；将其进行向量化后为：
$$X\beta =y$$
其中：
、、
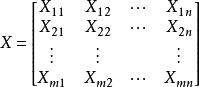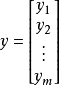
显然该方程组一般而言没有解，所以为了选取最合适的$\beta$ 让该等式"尽量成立"，引入残差平方和函数S:
$$S(\beta )=\Vert X\beta -y\Vert$$
当 $\beta =\hat{\beta }$时， 取最小值，记作：
$$\hat{\beta }=argmin(S(\beta ))$$
通过对 $S(\beta )$进行微分求最值,也就是矩阵对向量求导，可以得到：
$$X^{T}X\beta =X^{T}y$$
如果矩阵$X^{T}X$ 非奇异则 有唯一解:
$$\hat{\beta }=(X^{T}X\beta {)}^{-1}{X}^{T}y$$
但是这里依旧存在着这个问题，矩阵中都是没有常数项的，那我们怎们半呢。这里就不打公式了，就直接叙述，假如需要常数项，那么我们就需要在X矩阵的最右边添加以列全1，在$\beta$最后加上那个常数就可以了。

代码

好的，那门问题就此解决了，我们采用矩阵的方式撸了一份matlab和一份python的代码，可惜的是我手贱把matlab给删掉了。都怪他太占空间，我就忍不住删掉了。
Python版本：

import numpy as np
import pandas as pd
from matplotlib import pyplot as plt

file_path='./00.xlsx'
save_path='./pics/'
el = []
for i in range(6):
    df = pd.read_excel(file_path,sheet_name='Sheet'+str(i + 1), usecols=[0, 1, 2])
    df=np.array(df)
    # print (df)
    y, delta= df[:, 0], df[:, 1]
    y=np.expand_dims(y,-1)
    R=df[1][2]
    print(R)
    x=(delta**(3/2))*(4/3)*np.power(R,1/2)
    # print(x, y)
    print(x.shape, y.shape)
    xt=np.expand_dims(x,-1)
    # print(x.shape, xt.shape, y.shape)
    #print(x)
    e=1 / (np.matmul(x, xt))*np.matmul(x, y)
    e = e[0]
    el.append(e)
    y = y[:, 0]
    # print(x)
    lx = np.linspace(0, 1.1*max(x), 1000)
    # print(lx)
    ly = e * lx
    for t in range(2):
        if t==1:
            plt.plot(lx, ly, label='Fitted:$F_n$')
            # \frac{4}{3}\times{R^*}^{\frac{1}{3}}\times{\delta_n^{\frac{3}{2}}}
            plt.plot(x, y, 'ro', label=r'$x=\frac{4}{3}\times{R^*}^{\frac{1}{3}}\times{\delta_n^{\frac{3}{2}}}$')
            plt.plot(delta, y, 'bo', label='original data')
            plt.legend()
            plt.title("Sheet" + str(i + 1) + ":$F_n-x-{\delta}_n$")
            plt.savefig(save_path+"Sheet"+str(i+1)+"_1.jpg")
            plt.show()
        elif t==0:
            plt.plot(lx, ly, label='Fitted:$F_n$')
            # \frac{4}{3}\times{R^*}^{\frac{1}{3}}\times{\delta_n^{\frac{3}{2}}}
            plt.plot(x, y, 'ro', label=r'$x=\frac{4}{3}\times{R^*}^{\frac{1}{3}}\times{\delta_n^{\frac{3}{2}}}$')
            #plt.plot(delta, y, 'bo', label='original data')
            plt.legend()
            plt.title("Sheet" + str(i + 1) + ":$F_n-x$")
            plt.text(0.5*max(x), 0.2*max(y), "$E^* =$"+str(e),alpha=0.8)
            plt.text(-1, 3, r'$E^* =$',fontdict={ 'color': 'b'})
            plt.savefig(save_path + "Sheet" + str(i+1) + "_2.jpg")
            plt.show()
    # print(e)
print (el)

效果可以在拟合的曲线上画出来拟合的值，如下：