前面的章节基本上讲完了凸优化相关的理论部分,在对偶原理以及 KKT 条件那里我们已经体会到了理论之美!接下来我们就要进入求解算法的部分,这也是需要浓墨重彩的一部分,毕竟我们学习凸优化就是为了解决实际当中的优化问题。我们今天首先要接触的就是大名鼎鼎的梯度方法。现在人工智能和人工神经网络很火,经常可以听到反向传播,这实际上就是梯度下降方法的应用,他的思想其实很简单,就是沿着函数梯度的反方向走就会使函数值不断减小。
x k + 1 = x k − t k ∇ f ( x k ) , k = 0 , 1 , . . . x_{k+1}=x_{k}-t_k \nabla f(x_k),\quad k=0,1,... xk+1=xk−tk∇f(xk),k=0,1,...
上面的式子看起来简单,但是真正应用时你会发现有各种问题:
- 下降方向怎么选? ∇ f ( x k ) \nabla f(x_k) ∇f(xk) 吗?选择其他方向会不会好一点呢?
- 如果 f ( x ) f(x) f(x) (在某些点)不可导又怎么办呢?
- 步长 t k t_k tk 怎么选呢?固定值?变化值?选多大比较好?
- 收敛速度怎么样呢?我怎么才能知道是否达到精度要求呢?
- …
1. 凸函数
前面讲凸函数的时候我们提到了很多等价定义:Jensen’s 不等式、“降维打击”、一阶条件、二阶条件。这里我们主要关注其中两个:
- Jensen’s 不等式: f ( θ x + ( 1 − θ ) y ) ≤ θ f ( x ) + ( 1 − θ ) f ( y ) f(\theta x+(1-\theta) y) \leq \theta f(x)+(1-\theta) f(y) f(θx+(1−θ)y)≤θf(x)+(1−θ)f(y)
- 一阶条件等价于梯度单调性: ( ∇ f ( x ) − ∇ f ( y ) ) T ( x − y ) ≥ 0 for all x , y ∈ dom f (\nabla f(x)-\nabla f(y))^{T}(x-y) \geq 0 \quad \text { for all } x, y \in \operatorname{dom} f (∇f(x)−∇f(y))T(x−y)≥0 for all x,y∈domf
也就是说凸函数的梯度 ∇ f : R n → R n \nabla f: R^n\to R^n ∇f:Rn→Rn 是一个单调映射。
2. Lipschitz continuity
函数 f f f 的梯度满足**利普希茨连续(Lipschitz continuous)**的定义为
∥ ∇ f ( x ) − ∇ f ( y ) ∥ ∗ ≤ L ∥ x − y ∥ for all x , y ∈ dom f \|\nabla f(x)-\nabla f(y)\|_{*} \leq L\|x-y\| \quad \text { for all } x, y \in \operatorname{dom} f ∥∇f(x)−∇f(y)∥∗≤L∥x−y∥ for all x,y∈domf
也被称为 L-smooth。有了这个条件,我们可以推出很多个等价性质,这里省略了证明过程

也就是说下面的式子都是等价的
∥ ∇ f ( x ) − ∇ f ( y ) ∥ ∗ ≤ L ∥ x − y ∥ for all x , y ∈ dom f \|\nabla f(x)-\nabla f(y)\|_{*} \leq L\|x-y\| \quad \text { for all } x, y \in \operatorname{dom} f ∥∇f(x)−∇f(y)∥∗≤L∥x−y∥ for all x,y∈domf( ∇ f ( x ) − ∇ f ( y ) ) T ( x − y ) ≤ L ∥ x − y ∥ 2 for all x , y ∈ dom f (\nabla f(x)-\nabla f(y))^{T}(x-y) \leq L\|x-y\|^{2} \quad \text { for all } x, y \in \operatorname{dom} f (∇f(x)−∇f(y))T(x−y)≤L∥x−y∥2 for all x,y∈domf
f ( y ) ≤ f ( x ) + ∇ f ( x ) T ( y − x ) + L 2 ∥ y − x ∥ 2 for all x , y ∈ dom f f(y) \leq f(x)+\nabla f(x)^{T}(y-x)+\frac{L}{2}\|y-x\|^{2} \quad \text { for all } x, y \in \operatorname{dom} f f(y)≤f(x)+∇f(x)T(y−x)+2L∥y−x∥2 for all x,y∈domf
( ∇ f ( x ) − ∇ f ( y ) ) T ( x − y ) ≥ 1 L ∥ ∇ f ( x ) − ∇ f ( y ) ∥ ∗ 2 for all x , y (\nabla f(x)-\nabla f(y))^{T}(x-y) \geq \frac{1}{L}\|\nabla f(x)-\nabla f(y)\|_{*}^{2} \quad \text { for all } x, y (∇f(x)−∇f(y))T(x−y)≥L1∥∇f(x)−∇f(y)∥∗2 for all x,y
g ( x ) = L 2 ∥ x ∥ 2 2 − f ( x ) is convex g(x)=\frac{L}{2}\Vert x\Vert_2^2-f(x) \ \text{ is convex} g(x)=2L∥x∥22−f(x) is convex
Remarks 1:
上面的第 3 个式子
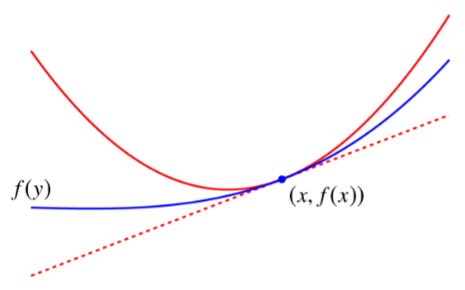
f ( y ) ≤ f ( x ) + ∇ f ( x ) T ( y − x ) + L 2 ∥ y − x ∥ 2 for all x , y ∈ dom f f(y) \leq f(x)+\nabla f(x)^{T}(y-x)+\frac{L}{2}\Vert y-x\Vert^{2} \quad \text { for all } x, y \in \operatorname{dom} f f(y)≤f(x)+∇f(x)T(y−x)+2L∥y−x∥2 for all x,y∈domf
实际上定义了一个二次曲线,这个曲线是原始函数的 Quadratic upper bound
并且由这个式子可以推导出
1 2 L ∥ ∇ f ( z ) ∥ ∗ 2 ≤ f ( z ) − f ( x ⋆ ) ≤ L 2 ∥ z − x ⋆ ∥ 2 for all z \frac{1}{2 L}\Vert\nabla f(z)\Vert_{*}^{2} \leq f(z)-f\left(x^{\star}\right) \leq \frac{L}{2}\left\Vert z-x^{\star}\right\Vert^{2} \quad \text { for all } z 2L1∥∇f(z)∥∗2≤f(z)−f(x⋆)≤2L∥z−x⋆∥2 for all z
这个式子中的上界 L 2 ∥ z − x ⋆ ∥ 2 \frac{L}{2}\left\|z-x^{\star}\right\|^{2} 2L∥z−x⋆∥2 带有 x ⋆ x^\star x⋆ 是未知的,而下界只与当前值 z z z 有关,因此在优化过程中我们可以判断当前的 f ( z ) f(z) f(z) 与最优值的距离至少为 1 2 L ∥ ∇ f ( z ) ∥ ∗ 2 \frac{1}{2 L}\|\nabla f(z)\|_{*}^{2} 2L1∥∇f(z)∥∗2,如果这个值大于0,那么我们一定还没得到最优解。Remarks 2:
上面的最后一个式子
( ∇ f ( x ) − ∇ f ( y ) ) T ( x − y ) ≥ 1 L ∥ ∇ f ( x ) − ∇ f ( y ) ∥ ∗ 2 for all x , y (\nabla f(x)-\nabla f(y))^{T}(x-y) \geq \frac{1}{L}\|\nabla f(x)-\nabla f(y)\|_{*}^{2} \quad \text { for all } x, y (∇f(x)−∇f(y))T(x−y)≥L1∥∇f(x)−∇f(y)∥∗2 for all x,y
被称为 ∇ f \nabla f ∇f 的 co-coercivity 性质。(这其实有点像 ∇ f \nabla f ∇f 的反函数的 L-smooth 性质,所以它跟 ∇ f \nabla f ∇f 的 L-smooth 性质是等价的)
3. 强凸函数
满足如下性质的函数被称为 **m-强凸(m-strongly convex)**的
f ( θ x + ( 1 − θ ) y ) ≤ θ f ( x ) + ( 1 − θ ) f ( y ) − m 2 θ ( 1 − θ ) ∥ x − y ∥ 2 for all x , y ∈ dom f , θ ∈ [ 0 , 1 ] f(\theta x+(1-\theta) y) \leq \theta f(x)+(1-\theta) f(y)-\frac{m}{2} \theta(1-\theta)\|x-y\|^{2} \quad \text { for all } x, y\in\text{dom}f,\theta\in[0,1] f(θx+(1−θ)y)≤θf(x)+(1−θ)f(y)−2mθ(1−θ)∥x−y∥2 for all x,y∈domf,θ∈[0,1]
m-强凸跟前面的 L-smooth 实际上非常像,只不过一个定义了上界,另一个定义了下界。
类似上面的 L-smooth 性质,我们课可以得到下面几个式子是等价的
f is m-strongly convex f \text{ is m-strongly convex} f is m-strongly convex( ∇ f ( x ) − ∇ f ( y ) ) T ( x − y ) ≥ m ∥ x − y ∥ 2 for all x , y ∈ dom f (\nabla f(x)-\nabla f(y))^{T}(x-y) \geq m\|x-y\|^{2} \quad \text { for all } x, y \in \operatorname{dom} f (∇f(x)−∇f(y))T(x−y)≥m∥x−y∥2 for all x,y∈domf
f ( y ) ≥ f ( x ) + ∇ f ( x ) T ( y − x ) + m 2 ∥ y − x ∥ 2 for all x , y ∈ dom f f(y) \geq f(x)+\nabla f(x)^{T}(y-x)+\frac{m}{2}\|y-x\|^{2} \quad \text { for all } x, y \in \operatorname{dom} f f(y)≥f(x)+∇f(x)T(y








 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 1331
1331

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








