计算入瞳、出瞳位置及孔径大小

一、概念

孔径光阑和视场光阑

孔径光阑：决定到达像的光能量大小的任何原件，限制入射光束的大小。

视场光阑：限制可以被系统成像的物的大小或角宽度的元件，限制了成像范围。

       孔径光阑控制从物点到共轭像点的光线的数目，视场光阑控制物点的个数。

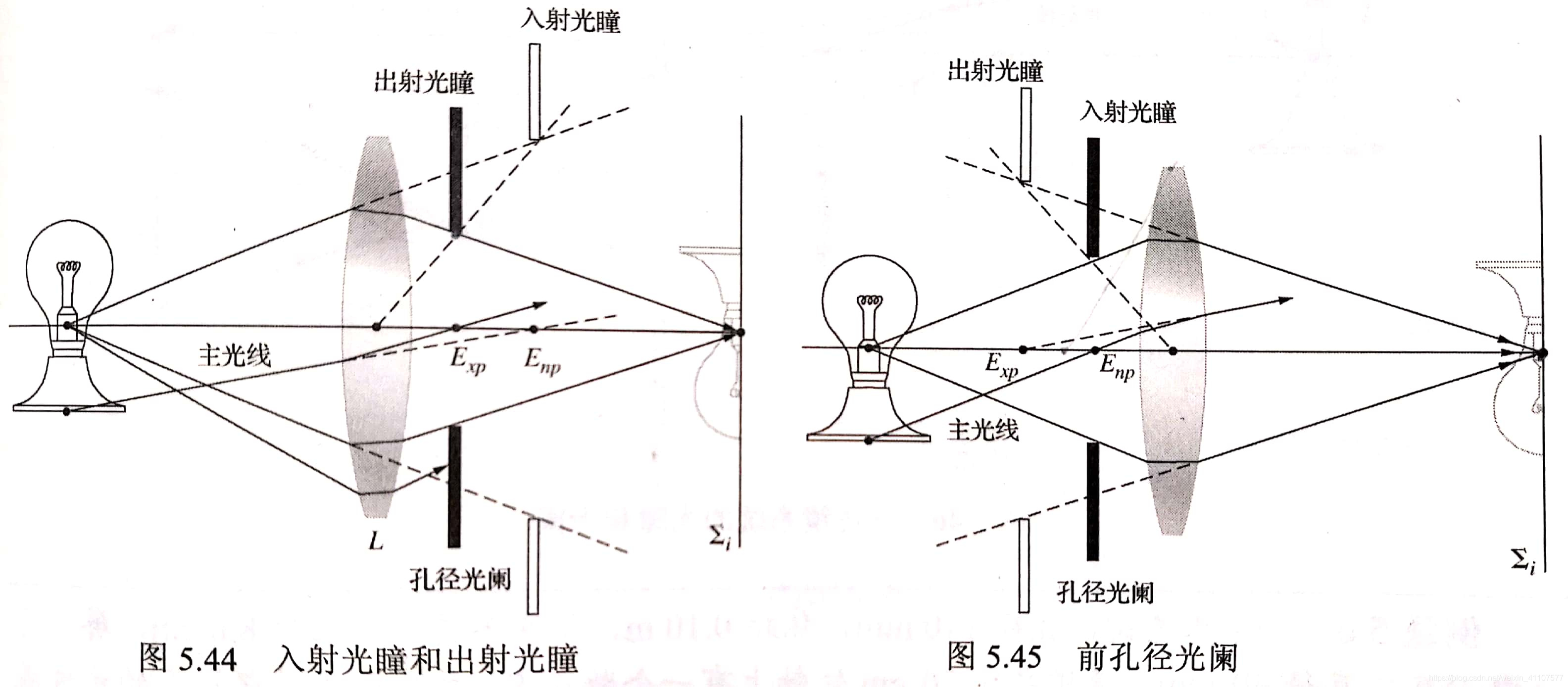
入射光瞳和出射光瞳

入射光瞳：从物上一轴上点穿越孔径光阑之前的元件看到的孔径光阑的像。

出射光瞳：从像上一轴上点穿过中间插入的透镜看到的孔径光阑的像。

       实际进入光学系统的光锥由入射光瞳决定，而离开光学系统的光锥由出射光瞳决定。

主光线和边缘光线

主光线：过孔径光阑中心的光线。

边缘光线：过孔径光阑边缘的光线。

特点：任一个物点的主光线一定会过孔径光阑、入瞳、出瞳的中心，其边缘光线一定会过孔径光阑、入瞳、出瞳的边缘。

 

 

 

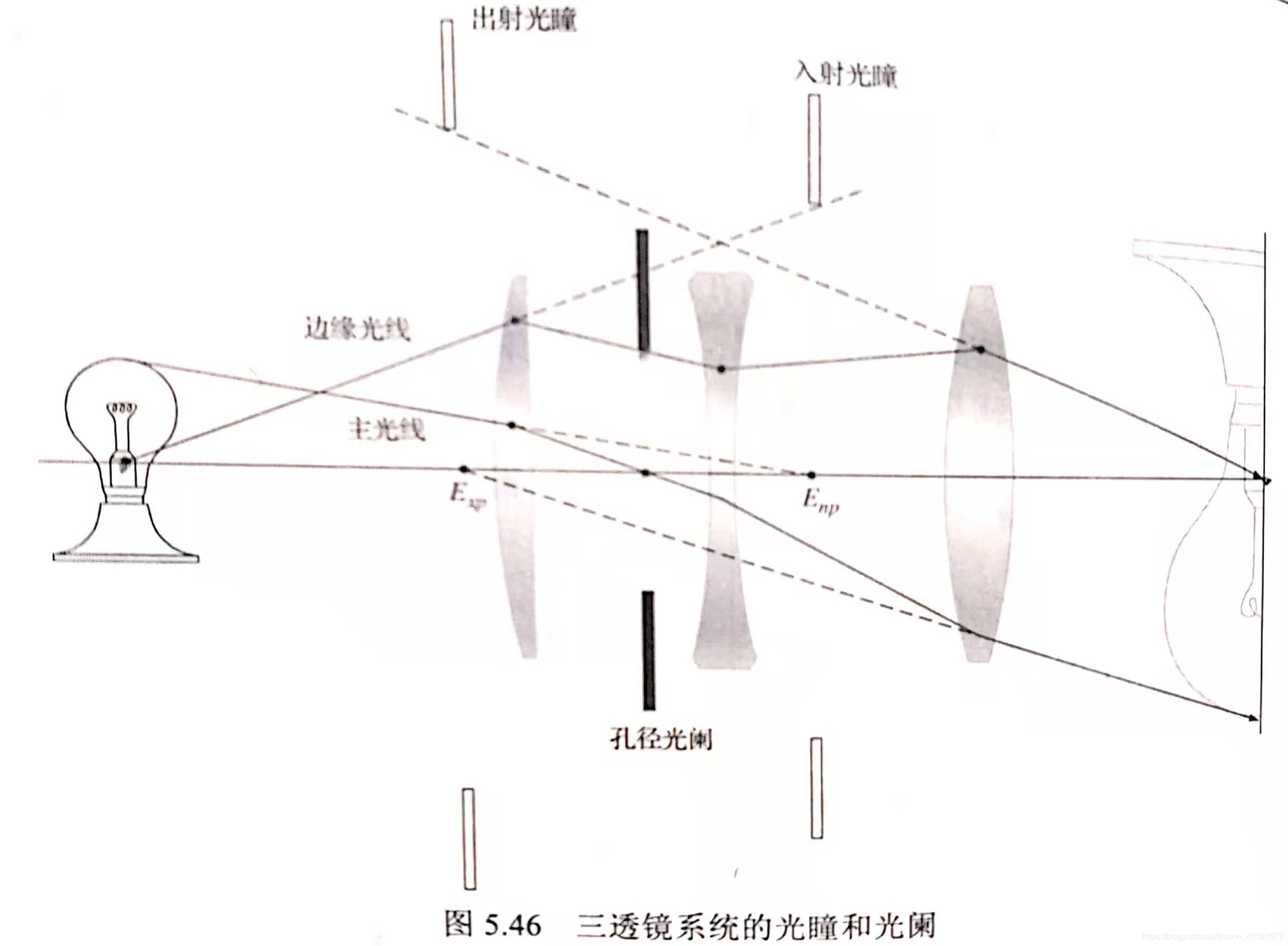
参考《光学》第五版 Eugene Hecht

 

二、工程实现

如何寻找孔径光阑？

对一近轴光线进行追迹，记录光线在每一个元件上的高度y和有效孔径CA，CA/y最小的就是代表孔径光阑的元件

如何寻找入瞳？

1. 计算入瞳位置

    将孔径光阑的中心看作是一个物点，向左进行追迹，得到第一个透镜面光线的高度y以及出射角u，(y/tan(u))+Δz可以计算出入瞳位置距第一个透镜面的距离(S0)。

2. 计算入瞳孔径

    将孔径光阑边缘看作是一个物点，向左进行追迹，得到第一个透镜面的光线高度y以及出射角u，(y/tan(u))-Δz可以计算出出射光线与光轴的交点距第一个透镜面的距离(S1)，可得该轴上点距入瞳中心的距离S=S0+S1，入瞳孔径R=S*tan(u)。

如何寻找出瞳？

1. 计算出瞳位置

    将孔径光阑的中心看作是一个物点，向右进行追迹，得到最后一个透镜面光线的高度y以及出射角u，(y/tan(u))+Δz可以计算出出瞳位置距最后一个透镜面的距离(S0)。

2. 计算出瞳孔径

     将孔径光阑边缘看作是一个物点，向右进行追迹，得到最后一个透镜面的光线高度y以及出射角u，(y/tan(u))-Δz可以计算出出射光线与光轴的交点距最后一个透镜面的距离(S1)，可得该轴上点距出瞳中心的距离S=S0+S1，出瞳孔径R=S*tan(u)。

参考《Modern Optical Engineering》