深入理解泊松分布、指数分布、正态分布

最新推荐文章于 2025-02-02 13:53:26 发布

王蒟蒻

最新推荐文章于 2025-02-02 13:53:26 发布

阅读量7.2k

点赞数 7

分类专栏： # 数学基础

本文链接：https://blog.csdn.net/weixin_41413511/article/details/116886274

版权

数学基础专栏收录该内容

6 篇文章

订阅专栏

各种分布怎么来的

当统计学家们开始研究概率分布时，他们看到，有几种形状反复出现，于是就研究他们的规律，根据这些规律来解决特定条件下的问题。

泊松分布

传送门
假设一个馒头店，老板想知道应该准备多少个馒头才能既不浪费又能充分供应？
如何采用均值的话不够好，有相当比例的时间不够卖。
于是老板思考采用其他的方法
在这里插入图片描述

把营业时间抽象为一根线段，把这段时间用T来表示，然后把周一的三个馒头（“甜在心馒头”，有褶子的馒头）按照销售时间放在线段上，根据分布把T 均分为四个时间段：
在这里插入图片描述
在每个时间段，就有点像抛硬币，要不是正面（卖出），要不是反面（没有卖出）

但是，如果把周二的七个馒头放在线段上，分成四段就不够了，因为每段时间可能卖出三个，可能卖出两个，这样的话就无法套用二项分布。

于是我们就将T切得越细越好
在这里插入图片描述因为P服从二项分布，故可得

经过计算化简得
其中

最后可得概率密度曲线
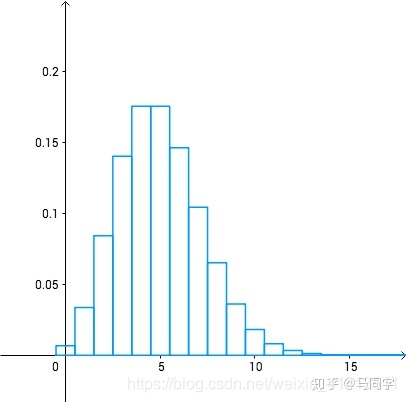
在这里插入图片描述
根据该密度曲线，老板可以得出如果每天准备8个馒头，则93%的情况下够用

指数分布

传送门

推导

还是以上面这个例子为例
我们现在要研究的是卖出馒头的时间间隔服从什么分布
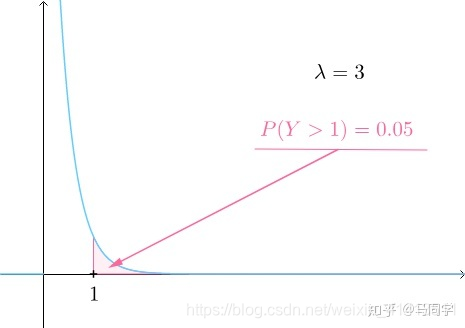
在这里插入图片描述比如算间隔大于1天的概率
即只需满足有一天没有卖出馒头
故
如何使任意间隔时间怎么算呢？
我们对泊松分布进行拓展，变为泊松过程
即可求得分布函数
求导即可得概率密度函数，即指数分布

指数分布的图像

在这里插入图片描述

泊松分布和指数分布的数学期望

在这里插入图片描述

为什么指数分布常常用来描述电器寿命

传送门

摘要

沉默成本

大概指的是已经付出的、且不可收回的成本。
针对这个概念有一个常见的说法：沉默成本不是成本
- 这句话的意思是，既然沉没成本不可收回，那么在做选择的时候就不应该考虑它。举一个简单的例子，买票去看电影，放映10分钟你就知道这是一部烂片，那么有两个选项：继续看或者走人。此时这张电影票已经消费了，没有办法收回，购买电影票的钱就是沉没成本。这个时候如果想离开电影院就直接离开，不要去考虑为这张电影票付出的金钱。

赌徒心理

有一个赌徒在赌大小，他一直在押“大”，可是台上连续出了十把“小”，让他输了很多钱：赌徒认为，前面出了那么多把“小”，再出“小”的可能性非常小了，他想把他的全部身家押“大”，搏一把翻本。
数学上可以证明，“扔了十把’小’条件下，下一把出‘大’”的概率和“扔一把就出‘大’”完全一样

几何分布无记忆性

可以通俗地解释为，前面十把输的钱是沉没成本，完全不影响之后出“大”的概率。赌徒应该及时抽身止损，保住最后一点身家。

指数分布的例子

上厕所问题
- 小明在自家小卖部苦苦等待第一位上门的客人，已经等待三个小时了：小明想去上厕所，可是只有憋着，因为它想到等了这么久了，客人上门的概率会随着时间的推移而不断提高，所以一定要等到客人之后再去上厕所。
- 实际上这种想法是错的，前面等的三个小时是沉没成本，不会影响之后的来客概率，该上厕所就去上厕所。
电器寿命
- 如果将电器考虑作理想的电器，器件不会老化。此时，电器的寿命是随机的。内部彷佛每秒钟都在扔硬币，扔到了正面，电器就坏了。在这种情况下，我们认为电器的寿命服从指数分布。
- 现实中是不会有理想电器的，但是如果只考虑短时间内的电器寿命，那么就可以将之视作理想电器，认为它的寿命服从指数分布。
- 故电器不是用得越久越容易坏