Überblick 本章节中的有些函数图像可能来自互联网/侵删
第4章 控制系统的频率特性
4.1 频率特性的概念
4.1.1 基本术语和概念的说明
第三章我们介绍了在时域内分析控制系统的一些方法。这样研究虽然十分直观符合人类的直觉,但是面对一些高阶系统往往十分的繁琐,因此我们从这一章开始利用一种全新的方法来研究控制系统的特性。
下面先给出一些术语的说明:
频率响应:控制系统对正弦输入信号的稳态响应,是时间响应的特例。
频率特性:是系统对不同频率正弦输入信号的响应特性。
频率特性分析法(频域法):是利用系统的频率特性来分析系统性能的方法,研究的问题仍然是系统的稳定性、快速性和准确性等,是工程上广为采用的控制系统分析和综合的方法。
下面我用自己的话来概括一下频域法:给系统一个正弦信号,系统在进入稳态以后也会输出一个同频率的正弦信号。我们分别研究输入输出的正弦信号的幅值比(幅频特性)和相位差(相频特性),并进一步得出各种奇奇怪怪的结论,这就是频域法。
实现频域法的数学工具是傅里叶变换。在第2章的学习笔记中,提到的那一篇说明傅里叶变换的物理意义的博客可以再看一下。在实际运(zuo)用(ti)过程当中,可以不用管其背后的数学要求,直接简单的把一个函数的拉普拉斯变换后的象函数内的
s
s
s用
j
ω
\mathrm{j}\omega
jω来代入,就可以得到这个函数傅里叶变换后的表达式了。
那么我们究竟应该如何求一个函数的幅频特性和相频特性呢?直接看公式:
幅频特性:
A
(
ω
)
=
∣
G
(
j
ω
)
∣
A(\omega)=|G(\mathrm{j}\omega)|
A(ω)=∣G(jω)∣
相频特性:
ϕ
(
ω
)
=
∠
G
(
j
ω
)
\phi(\omega)=\angle G(\mathrm{j}\omega)
ϕ(ω)=∠G(jω)
根据输入和输出是同频率的正弦函数,可以比较好地理解这两个公式。值得注意的是:
ϕ
<
0
\phi<0
ϕ<0的响应是滞后的,
ϕ
>
0
\phi>0
ϕ>0的响应是超前的。
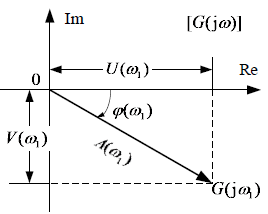
4.1.2 系统的频率特性的表现形式
我们可以将
G
(
j
ω
)
G(\mathrm{j}\omega)
G(jω)的实部和虚部分开,就可以将之表现为:
G
(
j
ω
)
=
U
(
ω
)
+
j
V
(
ω
)
G(\mathrm{j}\omega)=U(\omega)+\mathrm{j}V(\omega)
G(jω)=U(ω)+jV(ω)
其中
U
(
ω
)
U(\omega)
U(ω)是
G
(
j
ω
)
G(\mathrm{j}\omega)
G(jω)的实部,称为实频特性。
V
(
ω
)
V(\omega)
V(ω)是
G
(
j
ω
)
G(\mathrm{j}\omega)
G(jω)的虚部,称为虚频特性。
那么通过这两个新的概念的引入幅频特性和相频的特性的计算公式也可以存在其他的新的形式,但其实换汤不换药,不多啰嗦了。
4.1.3 系统的频率特性的求取
解析法:
如前文所述,只需要把拉普拉斯变换中的
s
s
s代入
j
ω
\mathrm{j}\omega
jω就可以得到系统频率特性。即:
G
(
j
ω
)
=
G
(
s
)
∣
s
=
j
ω
G(\mathrm{j}\omega)=G(s)|_{s=\mathrm{j}\omega}
G(jω)=G(s)∣s=jω
试验法:
1)改变输入谐波信号的频率,测出输出幅值与相移;
2)作出幅值对频率的函数曲线,此即幅频特性曲线;
3)作出相位移对频率的函数曲线,此即相频特性曲线。
4.2 极坐标图
极坐标图也被称为乃奎斯特(Nyquist))图或乃氏图。它的画法的原理非常简单,以系统的频率的特性的实频特性为横坐标,以频率的虚频特性为纵坐标。然后让
ω
\omega
ω从小到大进行变化,绘制出一系列的点,描点成线,获得极坐标图。
下面我们来讨论一下各典型环节的Nyquist图。
4.2.1 典型环节的Nyquist图
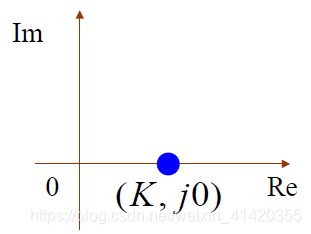
(1)比例环节
它的频率特性为:
G
(
j
ω
)
=
K
G(\mathrm{j}\omega)=K
G(jω)=K
很显然,在Nyquist图上它的图像就是一个点。
(2)积分环节
它的频率特性为:
G
(
j
ω
)
=
1
j
ω
=
−
j
1
ω
G(\mathrm{j}\omega)={1\over \mathrm{j}\omega}=-\mathrm{j}{1\over \omega}
G(jω)=jω1=−jω1
其实也比较显然,随着
ω
\omega
ω的不断增大,
G
(
j
ω
)
G(\mathrm{j}\omega)
G(jω)沿着虚轴不断靠近0点。

(3)微分环节
它的频率特性为:
G
(
j
ω
)
=
j
ω
G(\mathrm{j}\omega)=\mathrm{j}\omega
G(jω)=jω
没什么好多说的,和前面的积分环节差不多。

(4)惯性环节
它的频率特性为:
G
(
j
ω
)
=
K
1
+
j
T
ω
=
K
(
1
−
j
T
ω
)
1
+
T
2
ω
2
=
K
1
+
T
2
ω
2
−
j
K
T
ω
1
+
T
2
ω
2
G(\mathrm{j}\omega)={K\over 1+\mathrm{j}T\omega}={K(1-\mathrm{j}T\omega)\over 1+T^2\omega^2}={K\over 1+T^2\omega^2}-\mathrm{j}{KT\omega\over 1+T^2\omega^2}
G(jω)=1+jTωK=1+T2ω2K(1−jTω)=1+T2ω2K−j1+T2ω2KTω
不难发现,实部始终大于0,虚部始终小于0。可以得出极坐标图始终在第四象限的结论。随后取几个特殊点代入进行计算。。具体的计算过程这里就不体现了。值得一提的是,T要是等于1的话,这个图线应该是一个半圆弧。

(6)振荡环节
它的频率特性为:
G
(
j
ω
)
=
ω
n
2
ω
n
2
−
ω
2
+
j
2
ζ
ω
n
ω
G(\mathrm{j}\omega)={\omega^2_n\over\omega_n^2-\omega^2+\mathrm{j}2\zeta\omega_n\omega}
G(jω)=ωn2−ω2+j2ζωnωωn2
分子分母同除以
ω
n
2
\omega_n^2
ωn2,并令
λ
=
ω
ω
n
\lambda={\omega\over\omega_n}
λ=ωnω,得:
G
(
j
ω
)
=
1
1
−
λ
2
+
j
2
ζ
λ
=
1
−
λ
2
(
1
−
λ
2
)
2
+
4
ζ
2
λ
2
−
j
2
ζ
λ
(
1
−
λ
2
)
2
+
4
ζ
2
λ
2
G(\mathrm{j}\omega)={1\over 1-\lambda^2+\mathrm{j}2\zeta\lambda}={1-\lambda^2\over (1-\lambda^2)^2+4\zeta^2\lambda^2}-\mathrm{j}{2\zeta\lambda\over (1-\lambda^2)^2+4\zeta^2\lambda^2}
G(jω)=1−λ2+j2ζλ1=(1−λ2)2+4ζ2λ21−λ2−j(1−λ2)2+4ζ2λ22ζλ
这个时候还是用老师上课说的方法比较好。
∣
G
(
j
ω
)
∣
=
1
(
1
−
λ
2
)
2
+
4
ζ
2
λ
2
t
a
n
[
∠
G
(
j
ω
)
]
=
−
2
ζ
λ
1
−
λ
2
|G(\mathrm{j}\omega)|={1\over \sqrt{ (1-\lambda^2)^2+4\zeta^2\lambda^2}} \\\mathrm{tan}[\angle G(\mathrm{j}\omega)]=-{2\zeta\lambda\over {1-\lambda^2}}
∣G(jω)∣=(1−λ2)2+4ζ2λ21tan[∠G(jω)]=−1−λ22ζλ
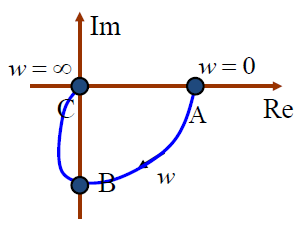
分别将
λ
=
0
,
1
,
∞
\lambda=0,1,\infty
λ=0,1,∞代入式中,最终可以绘制出草图:
(7)延时环节
它的频率特性为:
G
(
j
ω
)
=
e
−
j
τ
ω
=
c
o
s
τ
ω
−
j
s
i
n
τ
ω
G(\mathrm{j}\omega)=\mathrm{e}^{-\mathrm{j}\tau\omega}=\mathrm{cos}\tau\omega-\mathrm{j}\mathrm{sin}\tau\omega
G(jω)=e−jτω=cosτω−jsinτω
显然相频特性
∣
G
(
j
ω
)
∣
=
1
|G(\mathrm{j}\omega)|=1
∣G(jω)∣=1,幅频特性
∠
G
(
j
ω
)
=
−
τ
ω
\angle G(\mathrm{j}\omega)=-\tau\omega
∠G(jω)=−τω。
由此可以很简单地画出图像:

不难发现这是一个单位圆。
4.2.2 归纳总结
画Nyquist图的步骤
- 求幅频特性,相频特性
- 取 ω = 0 \omega=0 ω=0, ω = ∞ \omega=\infty ω=∞,来求Nyquist图的起点和终点。
- 再多找几个合适的点把诸如与坐标轴的交点,曲线的渐近线等等找出来。
- 据说还要判断曲线的弯曲方向(好麻烦哦)
两个小方法
乃氏图与实轴的交点即可以另实部等于0求得,也可以让相频特性等于
180
°
180\degree
180°的整数倍来求出。
类似地,我们也可以通过让相频特性等于
90
°
90\degree
90°的奇数倍来求得乃氏图和虚轴的交点。
多个传递函数相乘的形式
如果某系统的传递函数可以表示为如下形式:
G
(
s
)
=
∏
i
=
1
n
G
i
(
s
)
G(s)=\prod_{i=1}^nG_i(s)
G(s)=i=1∏nGi(s)
那么它的幅频特性和相频特性可以相应表示为:
A
(
ω
)
=
∏
i
=
1
n
∣
G
i
(
j
ω
)
∣
=
∏
i
=
1
n
A
i
(
ω
)
ϕ
(
ω
)
=
∑
i
=
1
n
ϕ
i
(
ω
)
A(\omega)=\prod_{i=1}^n|G_i(\mathrm{j}\omega)|=\prod_{i=1}^nA_i(\omega) \\\phi(\omega)=\sum^n_{i=1}\phi_i(\omega)
A(ω)=i=1∏n∣Gi(jω)∣=i=1∏nAi(ω)ϕ(ω)=i=1∑nϕi(ω)
这两个公式其实都非常的好理解,运用复数运算的基本性质也不难证明,这里就不多展开说明了。
4.2.3 系统的型次
机电系统的开环频率特性一般可表示为:
G
(
j
ω
)
=
K
(
j
ω
τ
1
+
1
)
(
j
ω
τ
2
+
1
)
…
(
j
ω
)
λ
(
j
ω
T
1
+
1
)
(
j
ω
T
2
+
1
)
…
G(\mathrm{j}\omega)={K(\mathrm{j}\omega\tau_1+1)(\mathrm{j}\omega\tau_2+1)\dots\over(\mathrm{j}\omega)^\lambda(\mathrm{j}\omega T_1+1)(\mathrm{j}\omega T_2+1)\dots}
G(jω)=(jω)λ(jωT1+1)(jωT2+1)…K(jωτ1+1)(jωτ2+1)…
λ
\lambda
λ等于几,我们就称这个系统为几型系统。
我们分三种情况来讨论上面这个式子。
乃氏图的低频段( K > 0 K>0 K>0)
考虑到当
ω
\omega
ω较小时,
j
ω
τ
i
+
1
\mathrm{j}\omega\tau_i+1
jωτi+1项或者
j
ω
T
i
+
1
\mathrm{j}\omega T_i+1
jωTi+1和1的相差不大,可以暂时忽略其对频率特性的影响,因此对系统其决定性作用的项是
K
(
j
ω
)
λ
K\over (\mathrm{j}\omega)^\lambda
(jω)λK。我们可以画出其在低频段的图像:

乃氏图的高频段
如果分母的阶次高于分子的阶次,则当
ω
→
∞
\omega\to\infty
ω→∞时,乃氏图曲线终止于坐标原点处;如果等于分子的阶次,则终止于坐标实轴上的有限值;如果低于,则会趋向于无穷。
为什么是实轴上的有线值?:因为不论是分子还是分母,实数项的系数的
ω
\omega
ω的次数总是大于虚数项的系数的
ω
\omega
ω的次数。
一般在系统频率特性分母上加极点,使系统相角之后;而在系统频率特性分子上加零点,使系统相角超前。
这又是为什么呢?:我的理解是(老师上课可能讲过但是我忘了不过我觉得我想的也很有道理):由于系统的时间常数一般为正值,对于分子上加零点而言,系统相当于乘上了一项
j
ω
τ
+
1
\mathrm{j}\omega\tau+1
jωτ+1。这一项的相位显然是正的,因此系统加上一个正的相位,于是就超前了。如果是加上一个极点的话,那么就是减去一个正的相位,于是就滞后了。
乃氏图的负频段
利用复数的运算法则可以比较容易的看出,对于 ω < 0 \omega<0 ω<0,系统的幅频特性不变,但是相频特性会变为原来的相反数,因此当 ω < 0 \omega<0 ω<0时,乃氏图是和 ω > 0 \omega>0 ω>0时的乃氏图关于实轴对称的。
总的来说,乃氏图画起来还是比较麻烦的,而且对系统进行了一些修正以后,系统的乃氏图就需要重新画过,为了解决这个问题,一个叫伯德的人发明了另外一种图。
4.3 对数坐标图
对数坐标图也被称为伯德图。
伯德图是将幅值对频率的关系和相位对频率的关系分别画在两张图上,用半对数坐标纸绘制。半对数坐标纸如下图所示:

在叙述绘图方法之前先引入一个单位叫做分贝。
n
(
d
B
)
=
20
l
g
N
n(\mathrm{dB})=20lgN
n(dB)=20lgN
如果我们将系统的幅值特性的单位转化为分贝,则可以得到如下的公式:
L
(
ω
)
=
20
l
g
∣
G
(
j
ω
)
∣
L(\omega)=20lg|G(\mathrm{j}\omega)|
L(ω)=20lg∣G(jω)∣
在绘制幅频特性的时候,图线的纵坐标用幅值(单位为分贝),横坐标为频率。但是注意由于是绘制在对数坐标纸上,所以相当于在绘图的过程中对频率进行了对数运算。这么做的一大好处在于:省纸。当然,更重要的好处在于,如此绘图可以让人们更直观的看到更多的频率和相频特性之间的关系。
其实我在学习的过程中一直有一个想法,其实伯德图的相频特性图线基本上就相当于把相频特性和频率绘制在一个双对数坐标纸上,只不过幅值我是通过计算的方式把他换算的线性尺度上。
在绘制相频特性的时候,纵坐标直接取相频特性的值,横坐标和幅频特性时的取法相同。
若 ω 2 = 10 ω 1 \omega_2=10\omega_1 ω2=10ω1则称从 ω 1 \omega_1 ω1到 ω 2 \omega_2 ω2为十倍频程。以dec.(decade)表示。
4.3.1 典型环节的伯德图
先说一下伯德图的特性:
1)若系统由多个环节串联而成,那么简单地把相位相加,幅值(dB)相加就好了。
2)由于横坐标的尺度是对数,因此
ω
=
0
\omega=0
ω=0的频率不能在伯德图上表现出来。实际绘图的时候起点可以根据实际所需的最低频率来决定。
3)根据输出幅值(dB)的定义我们不难发现,当
L
(
ω
)
=
0
L(\omega)=0
L(ω)=0时,输入和输出的幅值相等。
4)利用对数和复数的运算规律不难发现,传递函数互为倒数的伯德图关于横坐标轴相互对称。
4.3.1.1 比例环节
G
(
j
ω
)
=
K
∣
G
(
j
ω
)
∣
=
K
20
l
g
∣
G
(
j
ω
)
∣
=
20
l
g
K
∠
G
(
j
ω
)
=
0
°
G(\mathrm{j}\omega)=K \\|G(\mathrm{j}\omega)|=K \\20\mathrm{lg}|G(\mathrm{j}\omega)|=20\mathrm{lg}K \\\angle G(\mathrm{j}\omega)=0\degree
G(jω)=K∣G(jω)∣=K20lg∣G(jω)∣=20lgK∠G(jω)=0°
由此不难画出:

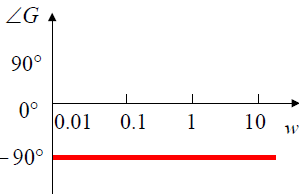
4.3.1.2 积分环节
G
(
j
ω
)
=
1
j
ω
∣
G
(
j
ω
)
∣
=
1
ω
,
∠
G
(
j
ω
)
=
−
90
°
G(\mathrm{j}\omega)={1\over \mathrm{j}\omega} \\|G(\mathrm{j}\omega)|={1\over \omega},\angle G(\mathrm{j}\omega)=-90\degree
G(jω)=jω1∣G(jω)∣=ω1,∠G(jω)=−90°
考虑幅值函数:
L
(
ω
)
=
−
20
l
g
ω
L(\omega)=-20\mathrm{lg}\omega
L(ω)=−20lgω
由于横坐标本质上是
l
g
ω
\mathrm{lg}\omega
lgω,所以图像体现在伯德图上是一条直线,不难画出:

相频特性也可以容易地画出:
4.3.1.3 微分环节
根据先前提到的性质可以得出,微分环节的伯德图应为积分环节的镜像,于是:

4.3.1.4 惯性环节
G
(
j
ω
)
=
1
1
+
j
T
ω
G(\mathrm{j}\omega)={1\over 1+\mathrm{j}T\omega}
G(jω)=1+jTω1
令
1
/
T
=
ω
T
1/T=\omega_T
1/T=ωT,可得:
G
(
j
ω
)
=
ω
T
ω
T
+
j
ω
G(\mathrm{j}\omega)={\omega_T\over \omega_T+\mathrm{j}\omega}
G(jω)=ωT+jωωT
我们先研究相频特性:
∠
G
(
j
ω
)
=
−
a
r
c
t
a
n
ω
ω
T
\angle G(\mathrm{j}\omega)=-\mathrm{arctan}{\omega\over\omega_T}
∠G(jω)=−arctanωTω
由此可以画出图像:
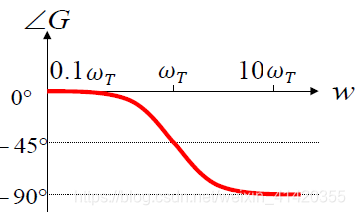
现在再来研究幅频特性:
∣
G
(
j
ω
)
∣
=
ω
T
ω
T
2
+
ω
2
L
(
ω
)
=
20
l
g
ω
T
−
20
l
g
ω
T
2
+
ω
2
|G(\mathrm{j}\omega)|={\omega_T\over\sqrt{\omega_T^2+\omega^2}} \\L(\omega)=20\mathrm{lg}\omega_T-20\mathrm{lg}\sqrt{\omega^2_T+\omega^2}
∣G(jω)∣=ωT2+ω2ωTL(ω)=20lgωT−20lgωT2+ω2
直接画这条曲线太过硬核,所以我们要采用近似的方法:
- 当 ω ≪ ω T \omega \ll \omega_T ω≪ωT时, L ( ω ) ≈ 20 l g ω T − 20 l g ω T = 0 d B L(\omega)\approx20\mathrm{lg}\omega_T-20\mathrm{lg}\omega_T=0dB L(ω)≈20lgωT−20lgωT=0dB。
- 当 ω ≫ ω T \omega \gg \omega_T ω≫ωT时, L ( ω ) ≈ 20 l g ω T − 20 l g ω L(\omega)\approx20\mathrm{lg}\omega_T-20\mathrm{lg}\omega L(ω)≈20lgωT−20lgω。这是一条直线,斜率为 − 20 d B / d e c -20dB/dec −20dB/dec。
- 当当 ω = ω T \omega = \omega_T ω=ωT时, L ( ω ) ≈ 0 L(\omega)\approx 0 L(ω)≈0。
我们称
ω
T
\omega_T
ωT为惯性环节的转折频率。
由此可以画出幅频特性的伯德图:

4.3.1.5 一阶微分环节
惯性环节的镜像:

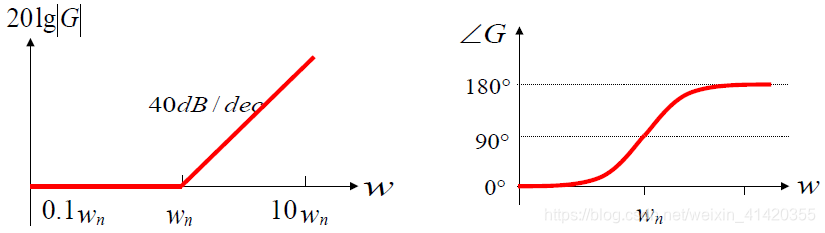
4.3.1.6 振荡环节
它的频率特性如下:
G
(
j
ω
)
=
ω
n
2
ω
n
2
−
ω
2
+
j
2
ζ
ω
n
ω
G(\mathrm{j}\omega)={\omega_n^2\over\omega_n^2-\omega^2+\mathrm{j}2\zeta\omega_n\omega}
G(jω)=ωn2−ω2+j2ζωnωωn2
令
λ
=
ω
ω
n
\lambda={\omega\over\omega_n}
λ=ωnω,可得:
G
(
j
ω
)
=
1
1
−
λ
2
+
j
2
ζ
λ
∣
G
(
j
ω
)
∣
=
1
(
1
−
λ
2
)
2
+
4
ζ
2
λ
2
∠
G
(
ω
)
=
−
a
r
c
t
a
n
2
ζ
λ
1
−
λ
2
G(\mathrm{j}\omega)={1\over1-\lambda^2+\mathrm{j}2\zeta\lambda} \\|G(\mathrm{j}\omega)|={1\over\sqrt{(1-\lambda^2)^2+4\zeta^2\lambda^2}} \\\angle G(\omega)=-\mathrm{arctan}{2\zeta\lambda\over1-\lambda^2}
G(jω)=1−λ2+j2ζλ1∣G(jω)∣=(1−λ2)2+4ζ2λ21∠G(ω)=−arctan1−λ22ζλ
我们采用研究惯性环节时的类似的方法用近似的手段来绘制振荡环节的图像:
- 当 ω ≪ ω n \omega\ll\omega_n ω≪ωn时, λ ≪ 1 \lambda\ll 1 λ≪1,有 ∣ G ∣ ≈ 1 → 20 l g L ( ω ) ≈ 0 d B |G|\approx1\to20\mathrm{lg}L(\omega)\approx0dB ∣G∣≈1→20lgL(ω)≈0dB。这是一条水平直线。
- 当
ω
≫
ω
n
\omega\gg\omega_n
ω≫ωn时,
λ
≫
1
\lambda\gg 1
λ≫1,有
∣
G
∣
≈
1
λ
4
+
4
ζ
2
λ
2
|G|\approx {1\over \sqrt{\lambda^4+4\zeta^2\lambda^2}}
∣G∣≈λ4+4ζ2λ21。由于
ζ
<
1
\zeta<1
ζ<1,所以
∣
G
∣
≈
1
λ
2
→
∣
L
(
ω
)
∣
=
−
40
l
g
λ
=
−
40
l
g
ω
+
40
l
g
ω
n
|G|\approx{1\over \lambda^2}\to|L(\omega)|=-40\mathrm{lg}\lambda=-40\mathrm{lg}\omega+40\mathrm{lg}\omega_n
∣G∣≈λ21→∣L(ω)∣=−40lgλ=−40lgω+40lgωn 。这是一条斜率为
−
40
d
B
/
d
e
c
-40dB/dec
−40dB/dec的直线。这样一来不难画出图像:

振荡环节的转折频率为 ω n \omega_n ωn。
下面研究相频特性:
∠ G ( ω ) = − a r c t a n 2 ζ λ 1 − λ 2 \angle G(\omega)=-\mathrm{arctan}{2\zeta\lambda\over1-\lambda^2} ∠G(ω)=−arctan1−λ22ζλ

4.3.1.7 二阶微分环节
二阶微分环节振荡环节的倒数。因此伯德图应该为振荡环节的镜像。
4.3.1.8 延时环节
由于延时环节不改变输出的幅值大小,只是让相位滞后,因此取对数后
L
(
ω
)
=
0
L(\omega)=0
L(ω)=0。
∠
G
\angle G
∠G为一条指数数曲线。

4.3.1.9 二重积分环节
G
(
j
ω
)
=
1
(
j
ω
)
2
→
L
(
ω
)
=
−
40
l
g
ω
G(\mathrm{j}\omega)={1\over(\mathrm{j}\omega)^2}\to L(\omega)=-40\mathrm{lg}\omega
G(jω)=(jω)21→L(ω)=−40lgω
∠
G
(
ω
)
=
180
°
\angle G(\omega)=180\degree
∠G(ω)=180°

4.3.2 一般系统伯德图作图方法
把这个系统拆分成各个基本环节,按照各个基本环节的作图方法先作出各个环节的伯德图(寻找转折频率,按照斜率画图等等),然后把作得的曲线叠加在一起,得到最终的结论。
4.3.3 最小相位系统
系统开环传递函数在S右半平面上既无极点,又无零点的系统,称为最小相位系统。否则称为非最小相位系统。
对于相同阶次的基本环节,当频率
ω
\omega
ω从
0
0
0变到
+
∞
+\infty
+∞时,最小相位的基本环节造成的相位移是最小的。(我也不知道为啥)
最小相位系统的相位在
ω
=
∞
\omega=\infty
ω=∞时,将变为
−
90
°
(
q
−
p
)
-90\degree(q-p)
−90°(q−p),
p
p
p和
q
q
q分别为传递函数中分子和分母多项式的次数。
4.4 由伯德图求系统传递函数
据说这个曾经在某一年补考的试卷上出现过。
具体求法如下图所示:
根据伯德图的作图过程可知,幅频曲线的转折点对应的频率是时间常数的倒数。我们下面按照系统的型次来讨论如何确定静态放大倍数。
0型系统低频段高度
0型系统的传递函数形如:
G
0
(
j
ω
)
=
K
0
(
τ
1
j
ω
+
1
)
(
τ
2
j
ω
+
1
)
…
(
T
1
j
ω
+
1
)
(
T
2
j
ω
+
1
)
…
G_0(\mathrm{j}\omega)={K_0(\tau_1\mathrm{j}\omega+1)(\tau_2\mathrm{j}\omega+1)\dots\over(T_1\mathrm{j}\omega+1)(T_2\mathrm{j}\omega+1)\dots}
G0(jω)=(T1jω+1)(T2jω+1)…K0(τ1jω+1)(τ2jω+1)…
分析这个式子我们不难发现,当
ω
→
0
\omega\to0
ω→0时,
G
(
j
ω
)
≈
K
0
G(\mathrm{j}\omega)\approx K_0
G(jω)≈K0,
∣
G
0
(
j
0
)
∣
=
K
0
|G_0(\mathrm{j}0)|=K_0
∣G0(j0)∣=K0。由此可以得到,0型系统的低频段的幅频特性高度为
20
l
g
K
0
20\mathrm{lg}K_0
20lgK0
1型系统低频段高度
1型系统的传递函数形如:
G
1
(
j
ω
)
=
K
1
(
τ
1
j
ω
+
1
)
(
τ
2
j
ω
+
1
)
…
j
ω
(
T
1
j
ω
+
1
)
(
T
2
j
ω
+
1
)
…
G_1(\mathrm{j}\omega)={K_1(\tau_1\mathrm{j}\omega+1)(\tau_2\mathrm{j}\omega+1)\dots\over \mathrm{j}\omega(T_1\mathrm{j}\omega+1)(T_2\mathrm{j}\omega+1)\dots}
G1(jω)=jω(T1jω+1)(T2jω+1)…K1(τ1jω+1)(τ2jω+1)…
如果系统各转交频率均大于1的画,那么1型系统幅频特性伯德图在
ω
=
1
\omega=1
ω=1处的高度为
20
l
g
K
1
20\mathrm{lg}K_1
20lgK1;如果有环节的转交频率小于1的话,我们就拿首段斜率为
−
20
d
B
/
d
e
c
-20dB/dec
−20dB/dec斜率线的延长线与
ω
=
1
\omega=1
ω=1线相交,交点的高度为
20
l
g
K
1
20\mathrm{lg}K_1
20lgK1。
不管各环节的转角频率怎么取,系统的幅频特性的首段斜率都为-20dB/dec。
首段直线和横坐标轴相交的交点值也不难获得,应为
K
1
K_1
K1。这很显然,不多说了。

2型系统低频段高度
2型系统的传递函数形如:
G
2
(
j
ω
)
=
K
2
(
τ
1
j
ω
+
1
)
(
τ
2
j
ω
+
1
)
…
(
j
ω
)
2
(
T
1
j
ω
+
1
)
(
T
2
j
ω
+
1
)
…
G_2(\mathrm{j}\omega)={K_2(\tau_1\mathrm{j}\omega+1)(\tau_2\mathrm{j}\omega+1)\dots\over (\mathrm{j}\omega)^2(T_1\mathrm{j}\omega+1)(T_2\mathrm{j}\omega+1)\dots}
G2(jω)=(jω)2(T1jω+1)(T2jω+1)…K2(τ1jω+1)(τ2jω+1)…
解法和1型系统一样,不过就是首段直线的斜率从
−
20
d
B
/
d
e
c
-20dB/dec
−20dB/dec变为了
−
40
d
B
/
d
e
c
-40dB/dec
−40dB/dec。相应的由于是2型系统所以和横坐标轴的交点坐标也由
K
1
K_1
K1变为了
K
2
\sqrt{K_2}
K2。

下面来总结一下:
首先根据低频段确定系统类型和开环增益。如果是水平线,那么是0型,斜率-20dB/dec,则是1型,以此类推。
然后观察渐进线斜率变化
如果斜率变化为-20dB/dec则存在一阶惯性,-40dB/dec则为二阶振荡。+20dB/dec,一阶微分。+40dB/dec,二阶微分。
4.5 获取频率特性的方法
由传递函数求取,由微分方程求取,实验法。
4.6 系统闭环频率特性
由开环频率特性估计闭环频率特性:
对于单位反馈系统:
X
o
(
j
ω
)
X
i
(
j
ω
)
=
G
(
j
ω
)
1
+
G
(
j
ω
)
{X_o(\mathrm{j}\omega)\over X_i(\mathrm{j}\omega)}={G(\mathrm{j}\omega)\over 1+G(\mathrm{j}\omega)}
Xi(jω)Xo(jω)=1+G(jω)G(jω)
通常来说,低频时:
∣
G
(
j
ω
)
∣
≫
1
∣
X
o
(
j
ω
)
X
i
(
j
ω
)
∣
=
∣
G
(
j
ω
)
1
+
G
(
j
ω
)
∣
≈
1
|G(\mathrm{j}\omega)|\gg1 \\\left|{X_o(\mathrm{j}\omega)\over X_i(\mathrm{j}\omega)}\right|=\left|{G(\mathrm{j}\omega)\over 1+G(\mathrm{j}\omega)}\right|\approx 1
∣G(jω)∣≫1∣∣∣∣Xi(jω)Xo(jω)∣∣∣∣=∣∣∣∣1+G(jω)G(jω)∣∣∣∣≈1
高频时:
∣
G
(
j
ω
)
∣
≪
1
∣
X
o
(
j
ω
)
X
i
(
j
ω
)
∣
=
∣
G
(
j
ω
)
1
+
G
(
j
ω
)
∣
≈
∣
G
(
j
ω
)
∣
|G(\mathrm{j}\omega)|\ll1 \\\left|{X_o(\mathrm{j}\omega)\over X_i(\mathrm{j}\omega)}\right|=\left|{G(\mathrm{j}\omega)\over 1+G(\mathrm{j}\omega)}\right|\approx |G(\mathrm{j}\omega)|
∣G(jω)∣≪1∣∣∣∣Xi(jω)Xo(jω)∣∣∣∣=∣∣∣∣1+G(jω)G(jω)∣∣∣∣≈∣G(jω)∣
如图所示:

4.7 系统频域性能指标
朗读并背诵全文
开环剪切频率
ω
c
\omega_c
ωc:开环频率特性幅值为1对应的频率。
闭环谐振频率
ω
r
\omega_r
ωr:产生谐振峰值对应的频率。
闭环谐振峰值
M
r
M_r
Mr:谐振频率处幅值的大小。
闭环截止频率
ω
b
\omega_b
ωb:对数幅频特性的幅值下降到
−
3
d
B
-3dB
−3dB时对应的频率,即幅值衰减
70
%
70\%
70%时的频率。其实也就是幅值变为
2
2
\sqrt{2}\over 2
22时的频率。
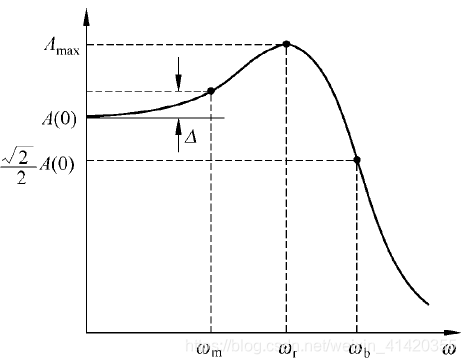
零频值
A
(
0
)
A(0)
A(0):对于单位负反馈系统,如果
A
(
0
)
=
1
A(0)=1
A(0)=1则说明系统输出对输入的跟随性好。
复现频率
ω
M
\omega_M
ωM,复现带宽
0
∼
ω
M
0\sim \omega_M
0∼ωM:在规定了
Δ
\Delta
Δ作为反映低频输入信号的允许误差后,则当系统幅频特性值与零频值
A
(
0
)
A(0)
A(0)只差第一次达到
Δ
\Delta
Δ时的频率,称为复现频率。

类似地我们也可以由截止带宽的概念。截止带宽也可以被简称为带宽。
4.8 机械系统的动刚度
这个概念在机械振动当中已经体现过了,这里就不说了。








 本文深入探讨了控制系统频率特性的概念,包括频率响应、频率特性和频率特性分析法。详细介绍了频率特性的表现形式、求取方法,以及极坐标图和对数坐标图的绘制技巧。分析了典型环节的频率特性,并提供了系统闭环频率特性的估算方法。
本文深入探讨了控制系统频率特性的概念,包括频率响应、频率特性和频率特性分析法。详细介绍了频率特性的表现形式、求取方法,以及极坐标图和对数坐标图的绘制技巧。分析了典型环节的频率特性,并提供了系统闭环频率特性的估算方法。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








