Überblick
第6章 控制系统的误差分析和计算
6.1 稳态误差的基本概念
系统过渡完成后的误差称为系统稳态误差。
稳态误差是系统在过渡完成后控制准确度的一种度量。
本章不研究因为静摩擦,零件质量的问题导致的静差,只研究由于系统不能很好地跟踪输入信号而引起地稳态误差,或者由于扰动而引起地稳态误差,即系统原理性误差。
6.1.1 稳态误差
定义:稳态误差是控制系统在输入信号作用下稳态输出的期望值与实际输出值之差。
设
x
o
r
(
t
)
x_{or}(t)
xor(t)是控制系统期望的输出值,
x
o
(
t
)
x_o(t)
xo(t)是其实际的输出值,则误差函数
e
(
t
)
e(t)
e(t)定义为:
e
(
t
)
=
x
o
r
(
t
)
−
x
o
(
t
)
e(t)=x_{or}(t)-x_o(t)
e(t)=xor(t)−xo(t)
稳态误差表示为:
lim
t
→
∞
e
(
t
)
=
lim
t
→
∞
[
x
o
r
(
t
)
−
x
o
(
t
)
]
\lim\limits_{t\to\infty}e(t)=\lim\limits_{t\to\infty}[x_{or}(t)-x_o(t)]
t→∞lime(t)=t→∞lim[xor(t)−xo(t)]
稳态误差直接表示了系统稳态控制的准确程度。
6.1.2 稳态偏差
研究下面这个系统:

定义:控制系统的偏差信号
ϵ
(
s
)
\epsilon (s)
ϵ(s)是系统的输入信号
X
i
(
s
)
X_i(s)
Xi(s)与系统的主反馈信号
Y
(
s
)
Y(s)
Y(s)之差。
也就是:
ϵ
(
s
)
=
X
i
(
s
)
−
Y
(
s
)
=
X
i
(
s
)
−
H
(
s
)
X
o
(
s
)
\epsilon(s)=X_i(s)-Y(s)=X_i(s)-H(s)X_o(s)
ϵ(s)=Xi(s)−Y(s)=Xi(s)−H(s)Xo(s)
根据终值定理,我们不难得到稳态偏差
ϵ
s
s
\epsilon_{ss}
ϵss为:
ϵ
s
s
=
lim
t
→
∞
ϵ
(
t
)
=
lim
s
→
0
s
ϵ
(
s
)
\epsilon_{ss}=\lim\limits_{t\to\infty}\epsilon(t)=\lim\limits_{s\to 0}s\epsilon(s)
ϵss=t→∞limϵ(t)=s→0limsϵ(s)
稳态偏差可以间接介表示系统稳态控制准确程度。
6.1.3 希望输出信号的确定
根据上面的定义,我们不难得到,当偏差信号 ϵ ( s ) = 0 \epsilon(s)=0 ϵ(s)=0时,希望输出信号 X o r ( s ) = X i ( s ) H ( s ) X_{or}(s)={X_i(s)\over H(s)} Xor(s)=H(s)Xi(s)。对于单位反馈系统: X o r = X i ( s ) X_{or}=X_i(s) Xor=Xi(s)。
6.1.4 误差信号与偏差信号的关系
误差信号 E ( s ) = ϵ ( s ) H ( s ) E(s)={\epsilon(s)\over H(s)} E(s)=H(s)ϵ(s)。对于单位反馈系统: E ( s ) = ϵ ( s ) E(s)=\epsilon(s) E(s)=ϵ(s)。
Zusammenfassend kann man sagen,
误差是从输出端定义,偏差是从输入端定义。两者之间的比例关系是 H ( s ) H(s) H(s)。对于单位反馈系统,两者则可以等同看待。值得主注意的是:只有稳定系统计算误差(偏差)才有定义。
6.2 输入引起的稳态误差
不难得出偏差的传递函数:
ϵ
(
s
)
X
i
(
s
)
=
1
1
+
G
(
s
)
H
(
s
)
{\epsilon(s)\over X_i(s)}={1\over 1+G(s)H(s)}
Xi(s)ϵ(s)=1+G(s)H(s)1
由此可得稳态偏差为:
ϵ
s
s
=
lim
t
→
∞
ϵ
(
t
)
=
lim
s
→
0
s
⋅
1
1
+
G
(
s
)
H
(
s
)
X
i
(
s
)
\epsilon_{ss}=\lim\limits_{t\to\infty}\epsilon(t)=\lim\limits_{s\to 0}s\cdot{1\over 1+G(s)H(s)}X_i(s)
ϵss=t→∞limϵ(t)=s→0lims⋅1+G(s)H(s)1Xi(s)
由
E
(
s
)
=
ϵ
(
s
)
H
(
s
)
E(s)={\epsilon(s)\over H(s)}
E(s)=H(s)ϵ(s)可得,若
H
H
H是常值,
e
s
s
=
ϵ
s
s
H
e_{ss}={\epsilon_{ss}\over H}
ess=Hϵss。若
H
=
1
H=1
H=1,则
e
s
s
=
ϵ
s
s
e_{ss}=\epsilon_{ss}
ess=ϵss
下面我们来分别研究0型,I型,II型系统。
G
(
s
)
=
K
(
τ
1
s
+
1
)
(
τ
2
s
+
1
)
…
s
v
(
T
1
s
+
1
)
(
T
2
s
+
1
)
…
G(s)={K(\tau_1s+1)(\tau_2s+1)\dots\over s^v(T_1s+1)(T_2s+1)\dots}
G(s)=sv(T1s+1)(T2s+1)…K(τ1s+1)(τ2s+1)…
反正下面有长长的一段推到。无论如何,记住下面这个稳态偏差表格就好了:
| 系统类别 | 单位阶跃 | 单位斜坡 | 单位加速度 |
|---|---|---|---|
| 0型 | 1 1 + K 1\over1+K 1+K1 | ∞ \infty ∞ | ∞ \infty ∞ |
| I型 | 0 0 0 | 1 K 1\over K K1 | ∞ \infty ∞ |
| II型 | 0 | 0 | 1 K 1\over K K1 |
这里讨论的是单位反馈系统。如果不是的话,算完以后记得再除以
H
(
0
)
H(0)
H(0)。
我们把做题过程捋一下:
- 首先判断系统的稳定性
- 把系统的传递函数(不包括反馈)化为标准形式。也就是多少多少s加1的连乘的形式。
- 按照系统的型次,和输入,对照表格,把K带进去计算系统的稳态偏差。
- 根据反馈的传递函数形式计算系统的稳态误差。
下面谈几个误差系数:
静态位置误差系数:
K
p
=
lim
s
→
0
G
(
s
)
K_p=\lim\limits_{s\to 0}G(s)
Kp=s→0limG(s),则
e
s
s
=
1
1
+
K
p
e_{ss}={1\over 1+K_p}
ess=1+Kp1
静态速度误差系数:
K
v
=
lim
s
→
0
s
G
(
s
)
K_v=\lim\limits_{s\to 0}sG(s)
Kv=s→0limsG(s),则
e
s
s
=
1
K
v
e_{ss}={1\over K_v}
ess=Kv1
静态加速度误差系数:
K
a
=
lim
s
→
0
s
2
⋅
G
(
s
)
K_a=\lim\limits_{s\to 0}s^2\cdot G(s)
Ka=s→0lims2⋅G(s),则
e
s
s
=
1
K
a
e_{ss}={1\over K_a}
ess=Ka1
6.3 干扰引起的稳态误差
我们研究如下包含干扰的系统:
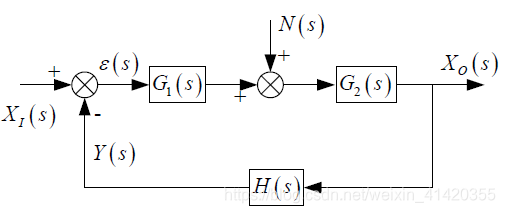
研究这个时候的系统偏差,可得系统的传递函数:

由此不难得出系统的闭环传递函数:
Φ
ϵ
N
(
s
)
=
ϵ
N
(
s
)
N
(
s
)
=
−
G
2
(
s
)
H
(
s
)
1
+
G
1
(
s
)
G
2
(
s
)
H
(
s
)
\Phi_{\epsilon N}(s)={\epsilon_N(s)\over N(s)}={-G_2(s)H(s)\over1+G_1(s)G_2(s)H(s)}
ΦϵN(s)=N(s)ϵN(s)=1+G1(s)G2(s)H(s)−G2(s)H(s)
当
X
i
(
s
)
=
0
,
N
(
s
)
≠
0
X_i(s)=0, N(s)\ne0
Xi(s)=0,N(s)=0时,产生的
−
X
o
(
s
)
⋅
H
(
s
)
-X_o(s)\cdot H(s)
−Xo(s)⋅H(s)称为扰动误差。
我们可以求得:
ϵ
s
s
n
=
lim
t
→
∞
ϵ
(
t
)
=
lim
s
→
0
s
ϵ
(
s
)
=
−
lim
s
→
0
G
2
H
1
+
G
1
G
2
H
N
(
s
)
e
s
s
n
=
ϵ
s
s
n
H
(
0
)
\epsilon_{ssn}=\lim\limits_{t\to\infty}\epsilon(t)=\lim\limits_{s\to 0} s\epsilon(s)=-\lim\limits_{s\to 0}{G_2H\over 1+G_1G_2H}N(s) \\e_{ssn}={\epsilon_{ssn}\over H(0)}
ϵssn=t→∞limϵ(t)=s→0limsϵ(s)=−s→0lim1+G1G2HG2HN(s)essn=H(0)ϵssn
也没啥道理,算就好了。我们需要记住系统扰动误差的传递函数。
6.4 减小系统误差的途径
- 系统的实际输出通过反馈环节与输入比较,因此反馈通道的精度对于减小系统误差至关重要;反馈通道元件的精度要高,避免在反馈通道引入干扰。
- 在保证系统稳定的前提下,对于输入引起的误差,可通过增大系统开环放大倍数和提高系统型次减小。
- 在保证系统稳定的前提下,对于干扰引起的误差,可通过在系统前向通道干扰点前加积分器和增大放大倍数减小。
- 有的系统要求的性能很高,既要求稳态误差小,又要求良好的动态性能。这时单靠加大开环放大倍数或串入积分环节往往不能同时满足上述要求,这时可采用复合控制的方法,或称顺馈的方法来对误差进行补偿。
这一节好像不考,我就把老师的ppt复制黏贴一下了。








 本文深入探讨了控制系统中的误差分析,包括稳态误差的概念、输入及干扰引起的误差、误差系数的计算,以及减小误差的途径。文章详细解释了稳态误差、偏差信号与误差信号的区别,提供了不同类型系统误差的计算方法。
本文深入探讨了控制系统中的误差分析,包括稳态误差的概念、输入及干扰引起的误差、误差系数的计算,以及减小误差的途径。文章详细解释了稳态误差、偏差信号与误差信号的区别,提供了不同类型系统误差的计算方法。
















 1314
1314

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








