文章目录
A x = 0 Ax=0 Ax=0 问题的求解
求解问题:

拉格朗日乘子方程:
L
(
x
,
λ
)
=
x
T
A
T
A
x
+
λ
(
1
−
x
T
x
)
L(x,\lambda)=x^TA^TAx+\lambda(1-x^Tx)
L(x,λ)=xTATAx+λ(1−xTx)
我们分别对
x
x
x和
λ
\lambda
λ求偏导数:

整理得:
A
T
A
x
=
λ
x
,
x
T
x
=
1
A^TAx=\lambda\ x,\ \ x^Tx=1
ATAx=λ x, xTx=1
由上式可知:
x
x
x为
A
T
A
A^TA
ATA的特征向量,且模长为1。
将A进行SVD分解:
A
=
U
Σ
V
T
,
A
T
A
=
V
Σ
T
U
T
U
Σ
V
T
=
V
Σ
T
Σ
V
T
A=U\mathrm{\Sigma}V^T,\ \ A^TA=V\mathrm{\Sigma}^TU^TU\mathrm{\Sigma}V^T=VΣ^TΣV^T
A=UΣVT, ATA=VΣTUTUΣVT=VΣTΣVT
可知:
V
V
V为
A
T
A
A^TA
ATA特征向量矩阵
∣
∣
A
x
∣
∣
2
=
x
T
A
T
A
x
=
x
T
λ
x
=
λ
x
T
x
=
λ
||Ax||^2=x^TA^TAx=x^Tλx=λx^Tx=\lambda
∣∣Ax∣∣2=xTATAx=xTλx=λxTx=λ
从而可知,当
x
x
x值为
A
T
A
A^TA
ATA的特征向量,
∣
∣
A
x
∣
∣
2
||Ax||^2
∣∣Ax∣∣2的值为对应的特征值。
因此 ∣ ∣ A x ∣ ∣ 2 = λ m i n ||Ax||^2= λ_{min} ∣∣Ax∣∣2=λmin, x x x为 λ m i n \lambda_{min} λmin对应 A T A A^TA ATA的特征向量。
在使用Eigen等库调用SVD接口时,一般会将奇异值按照从大到小的顺序排列,
因此问题的解x为V的最后一列。解的有效性条件,对应的 λ m i n \bm{\lambda}_{min} λmin非常接近于0
1)直接对A进行SVD分解,奇异值最小对应的V的列为解值。
2)对 A T A A^TA ATA进行SVD分解(相当于三角化),最小特征值对应的特征向量为解值。
H(单应矩阵homography),本质矩阵(Essential Matrix)和F(基础矩阵fundamental)
H矩阵适用于:1)特征点位于平面上;2)纯旋转,使用Faugeras 和 Lustman方法通过H阵解算出8种可能的
(
R
,
t
)
(R,t)
(R,t)
F使用于普通场景(非平面场景),但是从E/F中解算位姿有四种可能性,且不适用于低视差的场景。
因此单应矩阵H可以更好的应用于低视差(接近纯旋转)的场景下。而当平移接近零时,E和F阵则接近零(
E
=
t
∧
R
,
F
=
K
−
T
E
K
−
1
E=t^\land R,\ \ F=K^{-T}EK^{-1}
E=t∧R, F=K−TEK−1),很难从其中分离得到
R
R
R。
H阵中R与t是线性加和关系,而E和F中的
(
R
,
t
)
(R,t)
(R,t)是乘积关系,因此当t很小时,从E、F很难恢复出R和,而使用H阵,可以解算出
R
R
R,从而得到
t
t
t。
单应矩阵
【单应矩阵H】表征图像像素点之间的关系,即也反映【空间一点P】在【不同视角相机】下的【图像坐标】之间的关系。
使用条件是:
1)图像点对应的空间坐标处于同一平面;
2)两个图像对应相机坐标系只有旋转差(即两个相机的坐标系原点一致,或者同一相机经过旋转后得到的前后两张图像)。也即低视差场景。
设相机1与2是经过运动之后的不同的相机状态。
空间点P在相机1下的图像坐标为:

空间点P在相机1坐标系下对应的空间坐标为:

空间点P在相机2下的图像坐标为:

空间点P在相机2坐标系下的表示为:

相机1与相机2之间的运动表述为
R
,
T
{R,T}
R,T,则
X
1
X_1
X1与
X
2
X_2
X2之间的关系为
X
2
=
R
X
1
+
T
X_2=RX_1+T
X2=RX1+T
像素坐标与空间坐标之间的关系为:
x
1
=
1
z
1
K
X
1
→
X
1
=
z
1
K
−
1
x
1
x_1=\frac{1}{z_1}KX_1\rightarrow X_1=z_1K^{-1}x_1
x1=z11KX1→X1=z1K−1x1
x
2
=
1
z
2
K
X
2
→
X
2
=
z
2
K
−
1
x
2
x_2=\frac{1}{z_2}KX_2\rightarrow X_2=z_2K^{-1}x_2
x2=z21KX2→X2=z2K−1x2
1)平面场景
设平面在相机1坐标系下的表示为:
n
,
d
{n,d}
n,d,即平面方程为
n
T
x
=
d
n^Tx=d
nTx=d
示意图如下:

X
1
X_1
X1 满足上述公式:
n
T
X
1
=
d
→
1
d
n
T
z
1
K
−
1
x
1
=
1
n^TX_1=d\rightarrow\frac{1}{d}n^Tz_1K^{-1}x_1=1
nTX1=d→d1nTz1K−1x1=1
要求的结果形式:
x
2
=
H
x
1
x_2=Hx_1
x2=Hx1.
X
2
=
R
X
1
+
t
X_2=RX_1+t
X2=RX1+t
z
2
K
−
1
x
2
=
R
z
1
K
−
1
x
1
+
t
d
n
T
z
1
K
−
1
x
1
z_2K^{-1}x_2=Rz_1K^{-1}x_1+\frac{t}{d}n^Tz_1K^{-1}x_1
z2K−1x2=Rz1K−1x1+dtnTz1K−1x1
整理得:
x
2
=
z
1
z
2
K
(
R
+
t
d
n
T
)
K
−
1
x
1
x_2=\frac{z_1}{z_2}K\left(R+\frac{t}{d}n^T\right)K^{-1}x1
x2=z2z1K(R+dtnT)K−1x1
得:
H
=
z
1
z
2
K
(
R
+
t
d
n
T
)
K
−
1
H=\frac{z_1}{z_2}K\left(R+\frac{t}{d}n^T\right)K^{-1}
H=z2z1K(R+dtnT)K−1
2)纯旋转:
相机1与相机2之间的运动表述为
(
R
,
0
)
(R,0)
(R,0),则
X
1
X_1
X1与
X
2
X_2
X2之间的关系为:
X
2
=
R
X
1
⟹
z
2
K
−
1
x
2
=
R
z
1
K
−
1
x
1
⟹
x
2
=
z
1
z
2
K
R
K
−
1
x
1
X_2=RX_1\Longrightarrow z_2K^{-1}x_2=Rz_1K^{-1}x_1\Longrightarrow x_2=\frac{z_1}{z_2}KRK^{-1}x_1
X2=RX1⟹z2K−1x2=Rz1K−1x1⟹x2=z2z1KRK−1x1
⟹
x
2
=
H
x
1
,
H
=
z
1
z
2
K
R
K
−
1
\Longrightarrow x_2=Hx_1,\ \ H=\frac{z_1}{z_2}KRK^{-1}
⟹x2=Hx1, H=z2z1KRK−1
求解H步骤
x
2
=
H
x
1
x_2=Hx_1
x2=Hx1

图像齐次坐标引出尺度不变性,即:3维齐次坐标乘以非0常数,仍表示相同的二维坐标.

左右两侧同时叉乘
x
2
x_2
x2,将上式化为齐次方程:
x
2
×
H
x
1
=
0
x_2\times Hx_1=0
x2×Hx1=0
写成矩阵形式:

可化为:

写成齐次形式:

可转化为
A
H
=
0
AH=0
AH=0的形式:

可知一对点提供两个约束等式,单应矩阵9个元素,但由于齐次坐标的尺度不变性(
H
,
c
H
H,cH
H,cH(
c
c
c为非0常数)都代表同样的变换),则设立额外的条件方程:
∣
∣
H
∣
∣
2
=
1
||H||^2=1
∣∣H∣∣2=1,从而H矩阵只具有8个自由度,需4对点可求唯一解。
求解问题化为
x
x
x指代
H
H
H:

从而利用解法求解H矩阵。
ORB-SLAM求解H阵代码:
src/Initializer.cc cv::Mat Initializer::ComputeH21
A.at<float>(2*i,0) = 0.0;
A.at<float>(2*i,1) = 0.0;
A.at<float>(2*i,2) = 0.0;
A.at<float>(2*i,3) = -u1;
A.at<float>(2*i,4) = -v1;
A.at<float>(2*i,5) = -1;
A.at<float>(2*i,6) = v2*u1;
A.at<float>(2*i,7) = v2*v1;
A.at<float>(2*i,8) = v2;
A.at<float>(2*i+1,0) = u1;
A.at<float>(2*i+1,1) = v1;
A.at<float>(2*i+1,2) = 1;
A.at<float>(2*i+1,3) = 0.0;
A.at<float>(2*i+1,4) = 0.0;
A.at<float>(2*i+1,5) = 0.0;
A.at<float>(2*i+1,6) = -u2*u1;
A.at<float>(2*i+1,7) = -u2*v1;
A.at<float>(2*i+1,8) = -u2;
//SVD分解:w为奇异矩阵
cv::SVDecomp(A, w, u, vt, cv::SVD::MODIFY_A | cv::SVD::FULL_UV);
// 返回最小奇异值所对应的右奇异向量
// 注意前面说的是右奇异值矩阵的最后一列,但是在这里因为是vt,转置后了,所以是行;A有9列数据,故最后一列的下标为8
return vt.row(8).reshape(0, 3);
H矩阵的其他应用
单应矩阵H用来表征图像像素点之间的关系,可用于拼接平面图像或者纯旋转相机所得图像。
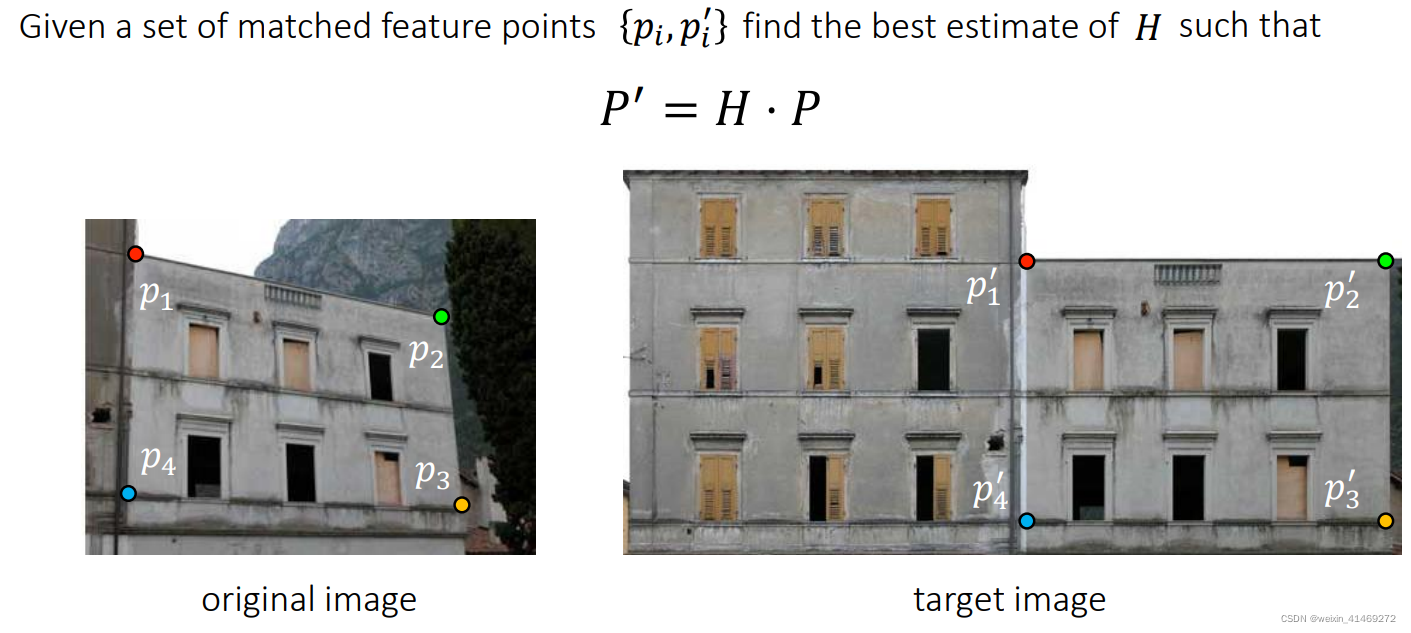
以上图片来自http://www.cs.cmu.edu/~16385/lectures/lecture9.pdf
本质矩阵与基础矩阵
【本质矩阵E】反映【空间一点P】在【不同视角相机】下【相机坐标系】中的表示之间的关系。
空间点P在相机1坐标系下对应的空间坐标为:

空间点P在相机2坐标系下的表示为:

X
1
X_1
X1和
X
2
X_2
X2的关系为:

【基础矩阵F】反映【空间一点P】在【不同视角相机】下的【图像坐标】之间的关系。
空间点P在相机1下的图像坐标为:

空间点P在相机2下的图像坐标为:

x
1
x_1
x1和
x
2
x_2
x2关系为:

则可知,F矩阵也同时具备齐次矩阵的尺度不变性
则位姿的估计步骤为:
- 根据配对点的像素位置,求出 E 或者 F;
- 根据 E 或者 F,求出
R
,
t
R,t
R,t。
E = t ∧ R , F = K − T E K − 1 E=t^\land R,\ \ F=K^{-T}EK^{-1} E=t∧R, F=K−TEK−1
F基础矩阵求解

可化为:

转化为AF=0的形式:

F矩阵每对点只能提供一个约束,且齐次坐标下的F也具备尺度不变性,从而可以加设条件:
∣
∣
F
∣
∣
2
=
1
||F||^2=1
∣∣F∣∣2=1,从而可以使用8对点完成F矩阵的求解。
另外由
E
=
t
∧
R
,
F
=
K
−
T
E
K
−
1
E=t^\land R,\ \ F=K^{-T}EK^{-1}
E=t∧R, F=K−TEK−1可计算得知
r
a
n
k
(
F
)
rank(F)
rank(F)为2,因而需要将上述求解到F矩阵的最小奇异值置为0,保证F的秩为2,得到最后的F。
求解方法同H阵。
使用SVD分解的方法求解
A
X
=
0
AX=0
AX=0方程:
A
=
U
D
V
T
A=UDV^T
A=UDVT
U
U
U是左奇异向量,它是一个8x8的 正交矩阵,
V
V
V是右奇异向量,是一个 9x9 的正交矩阵,
V
T
V^T
VT是
V
V
V的转置。
D
D
D是一个8 x 9 对角矩阵,除了对角线其他元素均为0,对角线元素称为奇异值,最小奇异值向量就是最优解(vt.row(8).reshape(0, 3)),设为
F
p
r
e
F_{pre}
Fpre。
要满足F矩阵秩为2的操作,需要再将
F
p
r
e
F_{pre}
Fpre进行SVD分解

将
F
p
r
e
F_{pre}
Fpre的最小奇异值
σ
3
\sigma_3
σ3置为0:

此外,使用E/F获得
R
,
t
R,t
R,t有以下四种可能:

ORB-SLAM求解H阵代码
src/Initializer.cc cv::Mat Initializer::ComputeF21
//构建A阵:
A.at<float>(i,0) = u2*u1;
A.at<float>(i,1) = u2*v1;
A.at<float>(i,2) = u2;
A.at<float>(i,3) = v2*u1;
A.at<float>(i,4) = v2*v1;
A.at<float>(i,5) = v2;
A.at<float>(i,6) = u1;
A.at<float>(i,7) = v1;
A.at<float>(i,8) = 1;
//SVD分解:w为奇异矩阵
cv::SVDecomp(A, w, u, vt,cv::SVD::MODIFY_A | cv::SVD::FULL_UV);
//得到Fpre
cv::Mat Fpre = vt.row(8).reshape(0, 3);
//置第三个特征值为0
cv::SVDecomp(Fpre,w,u,vt,cv::SVD::MODIFY_A | cv::SVD::FULL_UV);
w.at<float>(2)=0;
//重新组成F阵
return u*cv::Mat::diag(w)*vt;






















 5498
5498











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








