VINS预积分与误差模型

IMU的测量值误差模型

IMU的测量值误差模型：
$$\begin{array}{c}{\hat{a}}_t=a_t+R_w^t{g}^w+b_{a_t}+n_{a_t}\\ {\hat{\omega }}_t={\omega }_t+b_{{\omega }_t}+n_{{\omega }_t}\end{array}$$

其中，${\hat{a}}_t,{\hat{\omega }}_t$分别表示加速度计计陀螺仪的测量值；$b_{a_t},b_{{\omega }_t}$分别为加速度计，陀螺仪的零偏，该零偏是随机游走的，零偏的导数服从高斯分布，设为：

$${\dot{b}}_{a_t}=n_{b_a}和{\dot{b}}_{{\omega }_t}=n_{b_{\omega }}$$

${\hat{b}}_{a_t},{\hat{b}}_{{\omega }_t}$表示额定的零偏估计值。真实的零偏是包含了游走偏差的，而加速度计和陀螺仪需要体现实际的物理量，要去除噪声所带来的影响。
此外，$n_{a_t},n_{{\omega }_t}$ 分别为加速度计，陀螺仪的高斯噪声。$g^w$为重力加速度在世界坐标系下的表示。下标$t$表示t时刻。

据上述公式可知，IMU的测量误差主要由加速度计及陀螺仪的噪声及零偏的随机游走所构成。使用IMU的积分数据量来估计位姿，很难准确测量出随机偏差的真实值，从而影响IMU积分量。参考文献《Quaternion kinematics for the error-state Kalman filter》同样我们建立两套模型，一套真实模型(考虑随机噪声)，一套为估计模型(未考虑噪声，表示实际积分情况，用$\hat{\cdot }$表示)。

VINS预积分发生在两帧图像(关键)帧之间(如，$[k,k+1]$)，即将两帧图像发布时间内，IMU的数据进行积分(将[k,k+1]时刻内的IMU数据进行积分，从而得到IMU两帧图像之间的位姿变化量)。
因此状态的传递，误差的传递均是指两个图像帧之间的IMU积分值的传递，以下的预积分均以$[k,k+1]$为例。

IMU预积分真实模型

$$\begin{array}{c}{p}_{b_{k+1}}^w=p_{b_k}^w+v_{b_k}^w\mathrm{\Delta }{t}_k+\int {\int }_{t\in [k,k+1]}[R_t^w({\hat{a}}_t-b_{a_t}-n_{a_t})-g^w]d{t}^2\\ v_{b_{k+1}}^w=v_{b_k}^w+{\int }_{t\in [k,k+1]}[R_t^w({\hat{a}}_t-b_{a_t}-n_{a_t})-g^w]dt\\ q_{b_{k+1}}^w=q_{b_k}^w\otimes {\int }_{t\in [k,k+1]}\frac{1}{2}\mathrm{\Omega }({\hat{\omega }}_t-b_{{\omega }_t}-n_{{\omega }_t})q_t^{b_k}dt\end{array}$$

转换到体坐标系下，其PVQ形式如下：

其中：
$$\begin{array}{c}{\alpha }_{b_{k+1}}^{b_k}=\int {\int }_{t\in [t_k,t_{k+1}]}{R}_t^{b_k}({\hat{a}}_t-b_{a_t}-n_{a_t})d{t}^2\\ {\beta }_{b_{k+1}}^{b_k}={\int }_{t\in [t_k,t_{k+1}]}{R}_t^{b_k}({\hat{a}}_t-b_{a_t}-n_{a_t})dt\\ {\gamma }_{b_{k+1}}^{b_k}={\int }_{t\in [t_k,t_{k+1}]}\frac{1}{2}\mathrm{\Omega }({\hat{\omega }}_t-b_{{\omega }_t}-n_{{\omega }_t}){\gamma }_t^{b_k}dt\end{array}$$

在VIO系统中，IMU的发布频率通常是高于图像的，VINS系统中，使用k来表示对应的图像帧时刻，通过积分两个图像帧之间的IMU数据，来与视觉估计的位姿进行对比，来得到更加精确的位姿。

在连续积分模型时，时间连续，用$t$作为标识，而当使用实际离散积分形式时，$i$表示$k$到$k+1$图像帧之间的IMU发布时间。$b_k,b_{k+1}$为$k,k+1$时刻对应的IMU坐标系。
$$\begin{array}{cc}& {\alpha }_{i+1}^{b_k}={\alpha }_i^{b_k}+{\beta }_i^{b_k}\delta t+\frac{1}{2}{\overline{\alpha }}_i^{{}^{\prime }}\delta t^2\\ & {\beta }_{i+1}^{b_k}={\beta }_i^{b_k}+{\overline{\alpha }}_i^{{}^{\prime }}\delta t\\ & {\gamma }_{i+1}^{b_k}={\gamma }_i^{b_k}\otimes {\gamma }_{i+1}^i={\gamma }_i^{b_k}\otimes \left[\begin{array}{r}1\\ \frac{1}{2}{\overline{\omega }}_i^{{}^{\prime }}\delta t\end{array}\right]\end{array}$$

当使用普通离散增量形式时：
$${{\bar{a}}_i}^{\prime }={\hat{a}}_i-b_{a_i}-n_{a_i},{{\bar{\omega }}_i}^{\prime }={\hat{\omega }}_i-b_{{\omega }_i}-n_{{\omega }_i}$$
利用中值积分时，
$${{\bar{a}}_i}^{\prime }=\frac{1}{2}[q_i({\hat{a}}_i-b_{a_i}-n_{a_i})+q_{i+1}({\hat{a}}_{i+1}-b_{a_i}-n_{a_i})]$$$${{\bar{\omega }}_i}^{\prime }=\frac{1}{2}({\hat{\omega }}_i+{\hat{\omega }}_{i+1})-{\hat{b}}_{\omega }$$

IMU预积分估计模型

首先，不考虑高斯噪声，世界坐标系下的PVQ积分形式如下：
$$\begin{array}{c}{\hat{p}}_{b_{k+1}}^w={\hat{p}}_{b_k}^w+v_{b_k}^w\mathrm{\Delta }{t}_k+\int {\int }_{t\in [k,k+1]}[R_t^w({\hat{a}}_t-{\hat{b}}_{a_t})-g^w]d{t}^2\\ {\hat{v}}_{b_{k+1}}^w={\hat{v}}_{b_k}^w+{\int }_{t\in [k,k+1]}[R_t^w({\hat{a}}_t-{\hat{b}}_{a_t})-g^w]dt\\ {\hat{q}}_{b_{k+1}}^w={\hat{q}}_{b_k}^w\otimes {\int }_{t\in [k,k+1]}\frac{1}{2}\mathrm{\Omega }({\hat{\omega }}_t-{\hat{b}}_{{\omega }_t}){\hat{q}}_t^{b_k}dt\end{array}$$

转换到体坐标系下，其PVQ形式如下：
$$\begin{array}{c}{\hat{R}}_w^{b_k}{\hat{p}}_{b_{k+1}}^w={\hat{R}}_w^{b_k}\left({\hat{p}}_{b_k}^w+{\hat{v}}_{b_k}^w\mathrm{\Delta }{t}_k-\frac{1}{2}{g}^w\mathrm{\Delta }{t}_k^2\right)+{\hat{\alpha }}_{b_{k+1}}^{b_k}\\ {\hat{R}}_w^{b_k}{\hat{v}}_{b_{k+1}}^w={\hat{R}}_w^{b_k}({\hat{v}}_{b_k}^w-g^w\mathrm{\Delta }{t}_k)+{\hat{\beta }}_{b_{k+1}}^{b_k}\\ {\hat{q}}_w^{b_k}\otimes {\hat{q}}_{b_{k+1}}^w={\hat{\gamma }}_{b_{k+1}}^{b_k}\end{array}$$

其中：
$$\begin{array}{c}{\hat{\alpha }}_{b_{k+1}}^{b_k}=\int {\int }_{t\in [t_k,t_{k+1}]}{\hat{R}}_t^{b_k}({\hat{a}}_t-{\hat{b}}_{a_t})d{t}^2\\ {\hat{\beta }}_{b_{k+1}}^{b_k}={\int }_{t\in [t_k,t_{k+1}]}{\hat{R}}_t^{b_k}({\hat{a}}_t-{\hat{b}}_{a_t})dt\\ {\hat{\gamma }}_{b_{k+1}}^{b_k}={\int }_{t\in [t_k,t_{k+1}]}\frac{1}{2}\mathrm{\Omega }({\hat{\omega }}_t-{\hat{b}}_{{\omega }_t}){\gamma }_t^{b_k}dt\end{array}$$

其对应的实际离散积分形式：

当使用普通离散增量形式时：
$${{\bar{\hat{a}}}_i}^{\prime }={\hat{a}}_i-{\hat{b}}_{a_i},{{\bar{\hat{\omega }}}_i}^{\prime }={\hat{\omega }}_i-{\hat{b}}_{{\omega }_i}$$

利用中值积分时，
$${{\bar{\hat{a}}}_i}^{\prime }=\frac{1}{2}[{\hat{q}}_i({\hat{a}}_i-{\hat{b}}_{a_i})+{\hat{q}}_{i+1}({\hat{a}}_{i+1}-{\hat{b}}_{a_i})]$$$${{\bar{\hat{\omega }}}_i}^{\prime }=\frac{1}{2}({\hat{\omega }}_i+{\hat{\omega }}_{i+1})-{\hat{b}}_{{\omega }_i}$$

误差模型

在使用马氏距离构成最小二乘问题时，我们需要知道估计量随着时间的推移，其误差的一个变化情况，因而需要对误差模型进行评估，进而对其各变量的协方差进行评估。VINS用于构造滑窗约束方程。
设估计为$\hat{z}$，真值为$z$，则其误差定义为：
$$\delta z=z-\hat{z}$$

当选用$z_t^{b_k}=[{\alpha }_t^{b_k},{\beta }_t^{b_k},{\gamma }_t^{b_k},b_{a_t},b_{{\omega }_t}{]}^T$作为预积分参数，

普通增量积分

1. 其对应的普通增量积分的误差状态方程如下：
   $$\delta {\dot{z}}_t^{b_k}=\frac{\partial \delta z_t^{b_k}}{\partial \delta t}=J_t$$
   通过计算，可得$J_t=$
   
   从而得，当$\delta t$足够小时，
   
   
   在积分初始状态，设$J_0=I,P_0=0$，可以计算出雅可比矩阵$J_{t+\delta t}$及协方差矩阵$P_{t+\delta t}$随时间推移的传递方程。
   雅可比矩阵$J_{t+\delta t}$的传递方程：
   $$J_{t+\delta t}=\frac{\partial \delta z_{t+\delta t}^{b_k}}{\partial \delta t}=\delta {\dot{z}}_{t+\delta t}^{b_k}=\frac{\partial \delta z_{t+\delta t}^{b_k}}{\partial \delta z_t^{b_k}}\frac{\partial \delta z_t^{b_k}}{\partial \delta t}=F{J}_t=(I+F_t\delta t)J_t$$
   其中：
   $$\frac{\partial \delta z_{t+\delta t}^{b_k}}{\partial \delta z_t^{b_k}}=F=(I+F_t\delta t)$$
   设：变量$a\sim \mathcal{N}\left({\mu }_a,{\Lambda }_a\right),b\sim \mathcal{N}\left({\mu }_b,{\Lambda }_b\right)$
   则可知: $Fa\sim \mathcal{N}\left(F{\mu }_a,F{\Lambda }_a{F}^T\right),Gb\sim \mathcal{N}\left(G{\mu }_b,G{\Lambda }_b{G}^T\right)$
   从而得到协方差矩阵的传递公式：
   设误差量$\delta z_{b_t}^{b_k}\sim \mathcal{N}(0,P_t^{b_k})$,
   $$\delta z_{b_{t+\delta t}}^{b_k}\sim \mathcal{N}\left(0,P_{t+\delta t}^{b_k}\right)$$$$P_{t+\delta t}^{b_k}=\left(\mathrm{I}+F_t\delta t\right)P_t^{b_k}{\left(\mathrm{I}+F_t\delta t\right)}^T+\left(G_t\delta t\right)Q{\left(G_t\delta t\right)}^T$$
   当我们使用迭代法估计零偏时，零偏值会在每次迭代时，进行更新，从而我们的IMU积分量则需要根据新的零偏进行重新的计算，比较耗时，因而，VINS作者提出，通过更新IMU积分量对零偏误差的雅可比矩阵，来迭代零偏更新量到IMU的积分值，从而简化计算步骤。
   
   由$\delta z=z-\hat{z}$得：
   $$\frac{\partial z}{\partial b}=\frac{\partial \delta z}{\partial b}$$
   从而可以从$\frac{\partial \delta z_{t+\delta t}^{b_k}}{\partial \delta z_t^{b_k}}$对应的雅可比矩阵中拿出关于零偏的雅可比矩阵。
   注意：$\delta {\dot{z}}_{t+\delta t}^{b_k}$指的是对时间间隔$\delta t$的导数，而不是对 $\delta {\dot{z}}_t^{b_k}$的导数，这里与VINS代码有所不同(代码中使用的$J_t$矩阵取的对零偏的雅可比矩阵)

中值积分法

2. 使用中值积分法时，得到的状态方程传递方程如下：
   
   
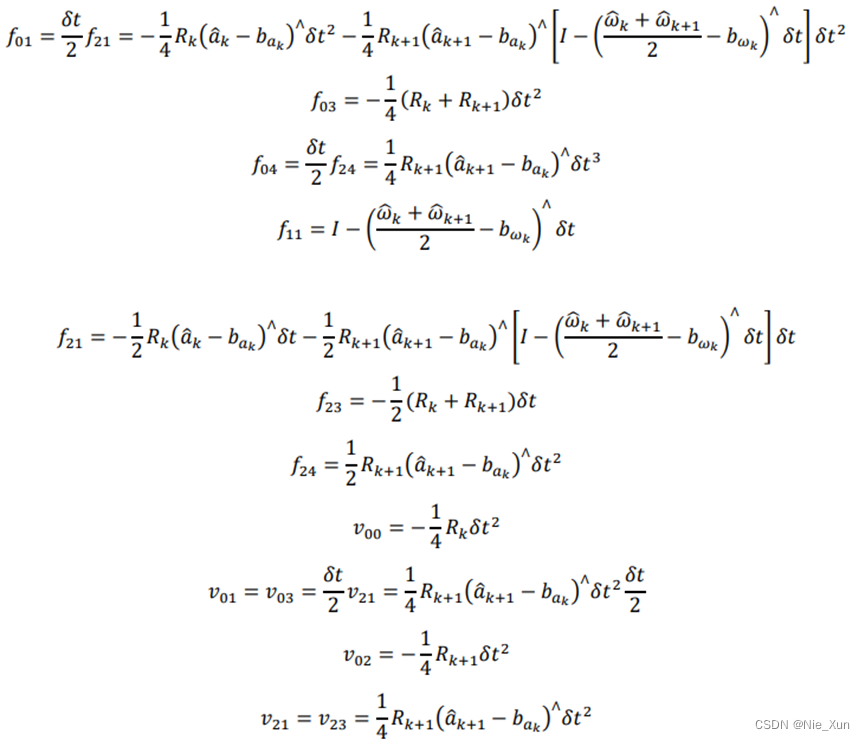
   以上图片来自《VINS 论文推导及代码解析 崔华坤》

参考文献

《VINS 论文推导及代码解析 崔华坤》
《VINS-Mono: A Robust and Versatile Monocular Visual-Inertial State Estimator》
《Quaternion kinematics for the error-state Kalman filter》