微分方程2_常微分方程、相空间

常微分方程例如：

函数的自变量只有一个，同城是时间t

一般用来描述相对变化量，代替求难以计算的绝对变化量

比如固定区域内两种种群的变化

和物理的力学中

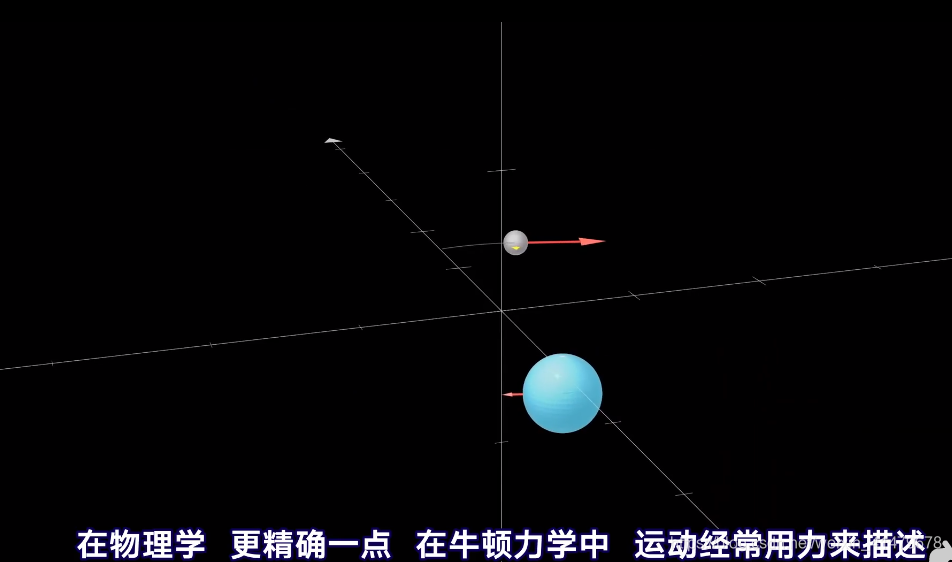
常微分方程代表随着一个变量引起的输出值变化的有限值的集合 比如时间变量

来看热身的例子

重力加速度给了物体向下的分量，大小为9.8m/s

把y坐标看成时间的函数

它的导数是速度的垂直分量

它的二阶导数就是重力加速度的垂直分量（红色直线代表的斜率向下，因此导数为负值）

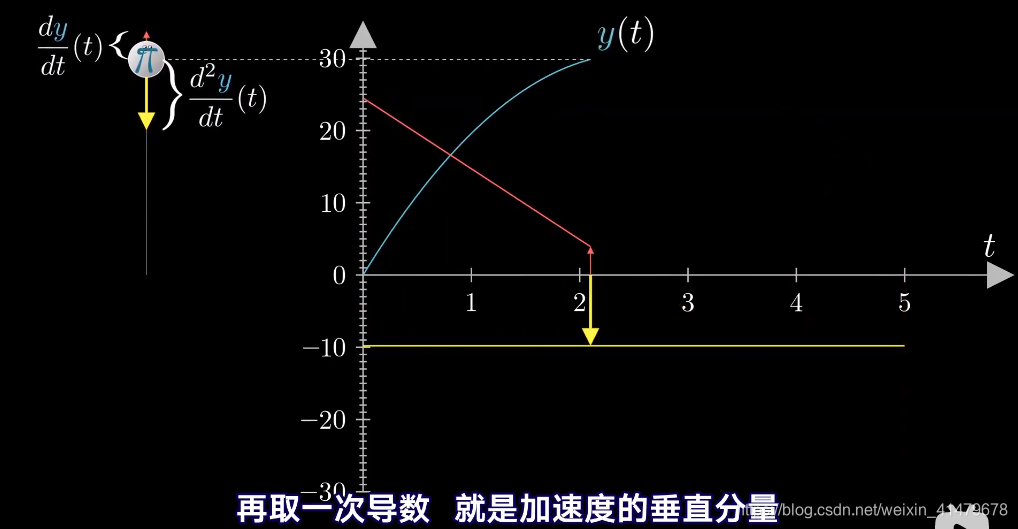
我们得到一个y’’(t)=-g的微分方程

那么-g的原函数是什么？


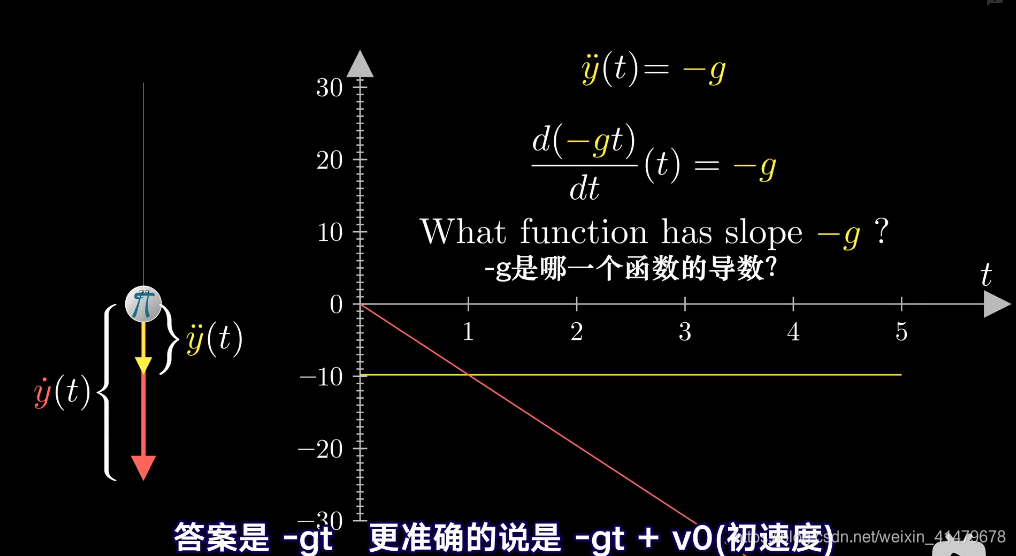
-g的函数有无穷多个，初速度$v_0$决定具体是哪一个

那么$-gt+v_0$又是哪一个函数的导数

也可以加一个常亮$y_0$，由初始位置决定

这样我们就通过有关函数的变化率，求出了原函数

这和之前学习过的微分方程，通常是通过一个函数的导数，二阶导数来求原方程的过程

例如普通的简谐运动

当初始角度较大时是不成立的


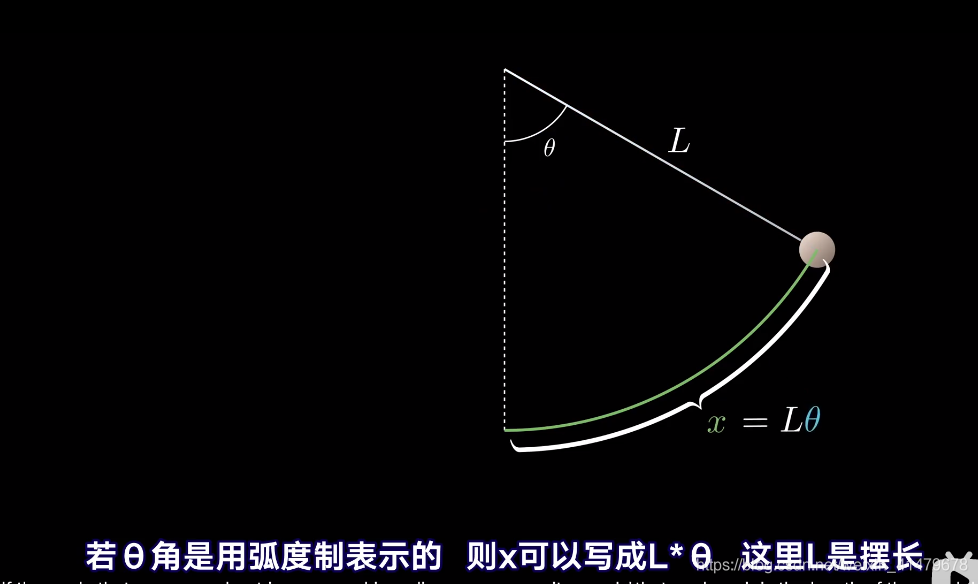
再加上一个运动方向上的分量g

而且可以证明粉色和黄色向量的夹角也等于$\theta$

那么$sin\theta =蓝色/黄色(-g)$

蓝色=$-g\ast sin\theta$

粉色=$-g\ast cos\theta$

x的二阶导数就是$-g\ast sin\theta$




考虑空气阻力

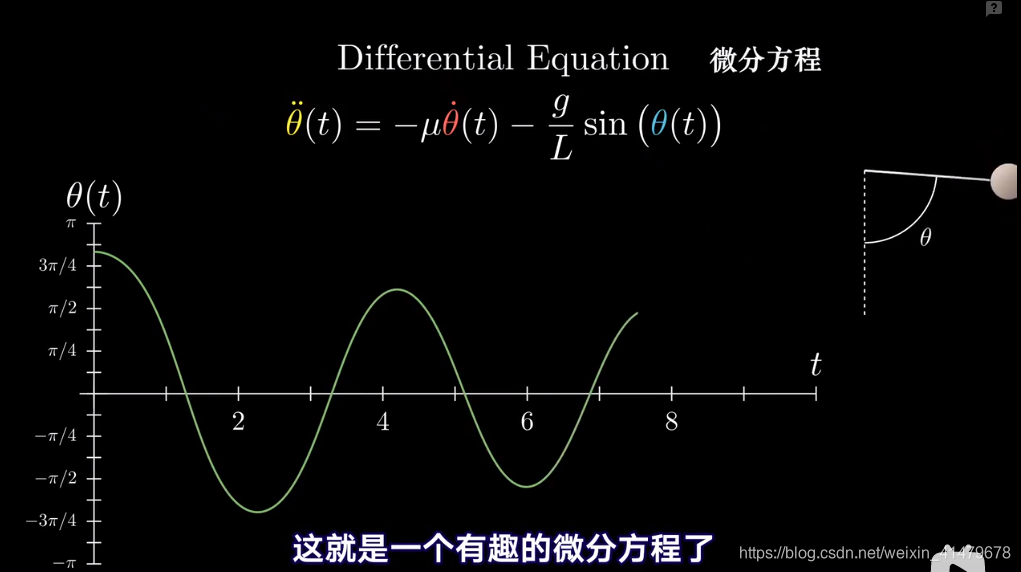
将这个方程放进向量场

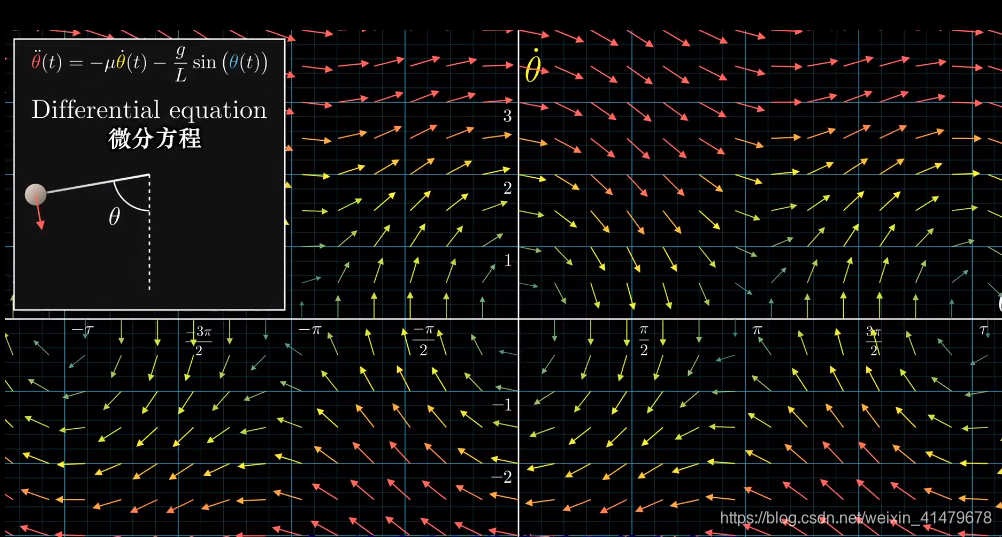
它的变化率就是变化趋势的大小和方向

用函数表示：

它的运动趋势

这个向量场还能体现出，当角度大于180时，小球需要赚几个圈才能进入旋涡

党阻力增大时，会更快进入旋涡

推广到任意常微分方程，都能用向量场空间来描述

这类问题通常过于复杂，如三体问题，我们需要18个维度来描述

我们把这样的空间称为 - 相空间 用来描述运动系统的所有状态空间


比如这个描述球体18个维度状态的空间叫做相空间

最后，用python求解单摆模型结束