浅谈辛普森悖论的应用

一.背景

我们日常运营工作中经常碰到的问题就是“为什么”，这个指标为什么在下降？那个指标为什么在变高？最终发现有些是“问题”，有些只是“数字”表现，并不是业务本质，为避免大家重复掉进这些不是问题的陷阱，本次为大家简单分享一下辛普森悖论的基础认知。

二.数据分析中违背常理的悖论：辛普森悖论

百度百科：当人们尝试探究两种变量（比如新生录取率与性别）是否具有相关性的时候，会分别对之进行分组研究。然而，在分组比较中都占优势的一方，在总评中有时反而是失势的一方。该现象于20世纪初就有人讨论，但一直到1951年，E.H.辛普森在他发表的论文中阐述此一现象后，该现象才算正式被描述解释。后来就以他的名字命名此悖论，即辛普森悖论。

定义：数据集分组呈现的趋势与数据集聚合整体呈现的趋势相反的现象。同一数据集的整体趋势和分组趋势有可能完全不同。在分组比较中占据优势的一方，在综合评估中却成为失势的一方，该现象被称为辛普森悖论。

1.辛普森悖论的数学原理

 

 从数学表达式上，我们可以看出，对 a、b、c、d 四个变量，分成 1 组和 2 组，在 1 组比率占优势的情况下，1组总体占优势却不成立。

若使用数学语言，辛普森悖论可以表示为如下的关系式：

当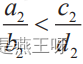，时，我们不能得出的结论，反过来也一样。

不少统计学家认为，由于辛普森悖论的存在，因此仅仅通过有限的统计数字，无法直接推导和还原事实真相。这是统计数据的致命缺陷。出现辛普森悖论的原因是因为这些数据中潜藏着一个魔鬼——潜在变量（lurking variable），因为数据可以按照各种形式分类分组和比较，潜在变量无穷无尽，理论上总是可以用某个潜在变量得到某种结论。比如在【人工问题解决率】的例子里，潜在变量有解决力高低不同的场景的样本占比。

2.一个实际例子

2.1【人工问题解决率】是不是在变坏

 现象：【人工问题解决率】由27周的86.7%到28周的86.4%，下降了0.3pp；

结论：我们的【人工问题解决率】在变坏；

2.2关于【人工问题解决率】的一种拆解

 【人工问题解决率】潜在变量：场景因素，将场景拆开分组来看，而两个分组场景，商品问题和履约问题的【人工问题解决率】都在上涨，都在变好，而整体却在下降，那“人工问题解决率在变坏”结论就有问题了～

白话一点：当你把数据拆开看的时候，分组和整体趋势会有完全不同的结论

当然，分组的结论也不能推理到总体，这是辛普森悖论很经典的案例。

3.如何避免出现辛普森悖论

如果要避免“辛普森悖论”给我们带来的误区，我们能做的，就是仔细认真地研究各种影响因素，不要笼统概括地看问题，尤其数据分析问题，拆解得越细，最终得到的效果越好。

比较流行的一种做法，就是需要斟酌个别分组的权重，以一定的系数去消除以分组资料基数差异所造成的影响。同时必须了解该情境是否存在其他潜在因素，需要进行综合性考虑。

3.1知道这种“陷阱”的存在

3.2耐心一点，不着急下结论，数据拆开再看看

3.3不仅仅是“异动”数据可以拆开去找原因解释，也有整体表现正常拆开后发现异动

最后还是要理解业务，最重要的就是积累沉淀，培养对业务的感觉，所有的数据表现理论上都可能存在这些问题，哪些需要拆开，哪些值得拆开，还是要基于对业务的充分理解。

三.服体应用的辛普森悖论：分组影响贡献值

1.分组影响贡献值计算原理

由数学公式推导而来（辛普森悖论，即分组数据比较时，需考虑分组权重变化因素）

解读：

一般一个业务指标对整体的变化影响会分为两部分：指标变化影响和分组业务量占比变化影响

指标变化影响：（分组KPI本期 - 分组KPI基期）*分组业务量占比本期

分组业务量占比变化影响（mix影响）：∑ （分组KPI基期*（分组业务量占比本期-分组业务量占比基期））

说明：

基期：即起始期 ；本期：即当期值；例如 对比W7和W6的变化，基期是W6，本期是W7。

计算周期维度单个分组成分对整体指标的影响（贡献值）：

指标变化影响=（本期指标-基期指标）*本期样本量占比

mix影响=基期指标 * （本期样本量占比-基期样本量占比）

贡献值=指标变化影响+mix影响

2.分组影响贡献值的缺陷

主要的缺陷来自于mix影响，这里仅考虑了分组业务量占比变化，未考虑分组相较整体是优秀的还是差劲的，未明确分组较整体是正向的还是负向的；

示例：

 数字表现&实际影响：

在基期情况下，【商品问题】的分母占比由31.0%下降至27.9%，因此mix波动带来负向影响-2.83%，=92.2%*（27.9%-31.0%）

但是它的实际影响并没有数字现的这么大；

在基期情况下，【履约问题】的分母占比由26.2%上涨至29.2%，因此mix波动带来正向影响2.40%，=80.1%*（29.2%-26.2%）

但是【履约问题】的【人工问题解决率】低于整体，它的占比上涨，理论上带来的是负向影响，与数字表现相悖；

在基期情况下，【团长咨询】的分母占比由4.5%下降至4.1%，因此mix波动带来负向影响0.29%，=67.8%*（4.1%-4.5%）

但是【团长咨询】的【人工问题解决率】低于整体，它的占比下涨，理论上带来的是正向影响，与数字表现相悖；

所以分组影响贡献值的mix影响有两点缺陷：1.影响大小与数字表现不一致，2.没有考虑分组较整体是好或坏；

四.辛普森悖论波动推导：因素波动贡献值

在业务场景中，当一个指标发生了变化，需要分析是哪些因素影响了指标？有时候正向影响和负向影响是同时存在的。作为运营同学，需要把这些因素找出来，并且量化其对于指标的影响值。

分析的结果无非两种：

1.各个因素对于指标的波动贡献率相差不大，说明该维度下各个因素表现基本相同，没有哪个因素有着影响指标变化的特殊意义

2.某个因素的波动贡献达到了50%+，而其他因素的贡献度很低，那么前面的因素是造成最后结果（上升或下降）的关键因素，就可以得出结论了

这里引入一个概念--波动贡献值，针对率的指标，来讨论一下如何计算各个因素对于指标波动的影响大小。

单一维度下，各因素的波动贡献值之和等于整体波动值。

各因素对率指标波动贡献值的计算

所谓率的指标，就是指标是由分子和分母构成，例如【人工非常不满意度】，【人工问题解决率】等等待。

1.事先定义：

基期分母，基期分子，基期率指标，本期分母，本期分子，本期率指标；

分组1～分组5，以及分组聚合的整体总和，如下图：

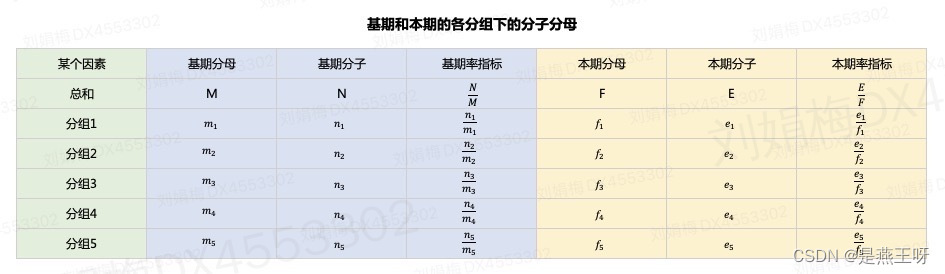
2.示例：【人工问题解决率】

美团优选人工客服的商品问题/履约问题/售后服务等10个场景，在人工服务结束后针对问题是否解决进行问卷调研，2022年27周（基期）此题回收评价量36090，其中评价已解决为29981，【人工问题解决率】29981/36090=83.07%；

2022年28周（本期）此题回收评价量上涨到36558，评价已解决为30239，【人工问题解决率】30239/36558=82.72%，下降 0.33pp；请问是哪个或哪些场景带来负向贡献，分别贡献多少？

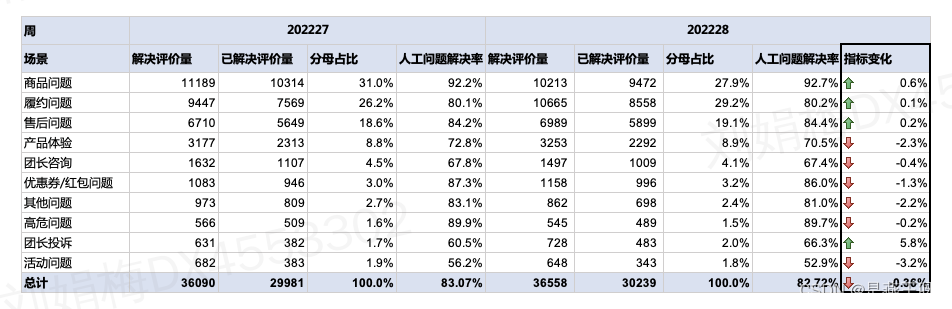
 大数据表面来看，指标下降主要来自两个方面：1.有6个场景指标变坏，2.履约问题（解决率低的场景）的评价量上涨，拖累了整体指标带来的结果。具体每个场景分别是正向或负向贡献，分别贡献多少，需要量化各个分组波动的贡献值。率值指标的波动值有两部分构成，分母分布波动和比例变化波动。

3.分母分布波动贡献

当总和分母M变成F的过程中，各个因素分母的分布也发生了变化。我们先控制各个因素的本期率值和基期率值保持一致。再计算各分组分母分布变化带来的波动值影响。同时我们引入一个中间分母，在本期分母总和F的前提下，各分组所占总和的比例与基期相同。

中间分母=F*m1/M，如下图所示

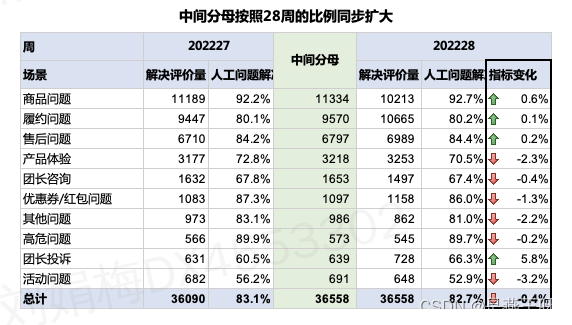
 那么每个分组的分母分布波动贡献=（基期指标-基期大盘指标）*（本期分母占比-基期分母占比）详见：https://blog.csdn.net/weixin_41875135/article/details/123506890--简化公式后

解释：上面的例子中，我们可以看到，

在基期情况下，【商品问题】的【人工问题解决率】高于整体，【商品问题】的分母（解决问题评价量）在基期所占整体评价的31%，但是在本期，占比为27.9%（10213/36558），优秀分组分布占比下降，因此该分组带来的波动贡献为负向（-0.28pp），

=（92.2%-83.1%）*（27.9%-31.0%）；

在基期情况下，【履约问题】的【人工问题解决率】低于整体，【履约问题】的分母（解决问题评价量）在基期所占整体评价的26.2%，但是在本期，占比为29.2%（10665/36558），较差分组占比上涨，因此该分组带来的波动贡献为负向（-0.09pp），

=（80.1%-83.1%）*（29.2%-26.2%）；

【分母波动贡献】与【分组mix影响】的逻辑区别：

应用	指标	判断权重变化	判断优秀or差劲
娟梅	分母波动贡献	是	是
服体	分组mix影响	是	否

【分母波动贡献】与【分组mix影响】的计算结果区别：

 解释：

【分母波动贡献】和【分组mix影响】的影响值总计是一致的，都是-0.33%，因为【分母波动贡献】除了考虑权限之外，还考虑了分组较整体是好或坏，高于整体为优秀，低于整体为较差；

分母波动贡献的推导逻辑是：假设各分组的【人工问题解决率】保持不变的情况下，各分组分母分布的波动，使整体指标下降了0.33pp，但是我们实际整体是下降了0.36pp，另外0.03pp为率值值波动的另外一个组成部分带来的。

4.指标变化贡献

指标变化贡献与服体和指标变化影响是一致的。

这部分很好理解，由于各分组的率值发生了变化，在分母不变的情况下，计算该部分的波动值。那么每个分组的指标变化贡献=（本期指标-基期指标）*本期分母占比，例如下图：

 解释：

【商品问题】，本期【人工问题解决率】92.7%，比基期92.2%要高，所以带来的波动为正向（+0.16pp），=（92.7%-92.2%）*27.9%；

【产品体验】，本期【人工问题解决率】70.5%，比基期72.8%要低，所以带来的波动为负向（-0.21pp），=（70.5%-72.8%）*8.9%；

因此指标部化这部分的波动，使用整体指标下降了0.03pp.

5.整体波动贡献

整体波动贡献将以上两个部分的波动贡献值加在一起即可（贡献值=分母分布波动贡献+指标变化贡献），如下图：

 整体【人工问题解决率】下降0.36pp，其中【产品体验】带来负向贡献0.22pp，【商品问题】带来负向贡献0.12pp。因此可以得出结论，整体【人工问题解决率】从83.07%下降到82.72%，这一下降是由于【产品体验】和【商品问题】导致的。其中【产品体验】是由于指标下降带来负向贡献，【商品问题】是由于发生上涨带来负向贡献。

在日常运营工作中，需要知道率值波动是由两方面的影响带来的，并且它们分别是怎样的，才能定位到异动的原因。

这里是介绍单个维度下各分组对于关键指标的影响，但是在实际工作中，我们的指标受多个维度因素的影响。那我们如何去评估不同维度对于指标变化的影响大小呢，如何快速的定位是哪个维度下，哪个因素对于指标的影响最大呢？

五.课堂练习