系统梳理EEG中常用的功能连接指标—系列2（终）

《本文同步发布于“脑之说”微信公众号，欢迎搜索关注~~》

在上一篇文章《系统梳理EEG中常用的功能连接指标—系列1》中，笔者对皮尔森相关系数（Pearson correlation coefficient）、波谱相干（Spectral coherence）、互信息（Mutual information,MI）、相锁值（Phase Locking Value, PLV）4个功能连接指标的计算方法、优缺点进行了介绍。本文为系列2，继续对相关的功能连接指标进行梳理。

5.相滞指数（Phase lag index，PLI）
与PLV相似，PLI也是基于相位的功能连接方法，可以用来测量两个通道信号的相同步程度，其计算方法如下：
其中，N表示时间点，φrel表示两个通道信号在时间tn处的相位差，sign是一个符号函数，当自变量为正值时其输出为1，当自变量为负值时其结果为-1，对于0其结果也是0.
PLI的取值范围为[0 1]，值越大表示两个信号之间的相位同步程度越强。PLI最主要的优点是对体积传导效应（volume conduction effect）不敏感，但是其对噪声似乎比较敏感。

6.部分有向相干（Partial directed coherence, PDC）
PDC是一种基于格兰杰因果关系的多变量有效连接测量方法，与前面介绍的其他功能连接方法不同，PDC是测量通道信号之间的因果影响，因此是有方向性的。对于一个N通道的EEG信号X(n)=[x1(n),x2(n), x3(n), …, xN(n)]T，其可以用一个多变量的自回归模型MVAR来描述：

其中p是MVAR的order，Ar表示系数矩阵，W(n)表示高斯白噪声。
p可以通过Akaike information criterion (AIC)来求解，而通过Yule-Walker方程，可以把Ar求解出来。当求得Ar之后，那么就可以得到A(f):

其中I表示identity matrix。
那么，频率f处从通道j到通道i的有向信息流即PDC值可以用以下公式来求解：

其中Aij(f)表示A(f)矩阵的元素，*表示矩阵转置和复共轭。
PDC值的范围[0 1]，值越大表示从通道j到i的信息流动越强

7.有向传递函数（Direct Transfer Function, DTF）
与PDC类似，DTF也是一种基于格兰杰因果关系的多变量有效连接测量方法，DTF的计算过程也与PDC类似，唯一区别在于DTF的计算用到了上述A(f)的逆矩阵，我们这里记为H(f)，那么DTF定义为：

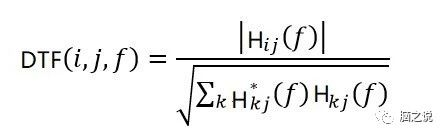
同样，DTF取值范围在[0 1]。与PDC相比，DTF主要问题可能是会检测到通道之间的间接因果连接，因此会产生虚假连接，而PDC只检测通道之间的直接连接。

8.其他功能连接指标
除了在《系列1》和本文上述介绍的这些功能连接指标，还有很多其他的功能连接的指标，如同步似然指数（Synchronization Likelihood, SL）、转移熵（Transfer Entropy, TE）、部分转移熵（Partial Transfer Entropy, PTE）、相位斜率指数(Phase Slope Index, PSI)、加权PLI（Weighted Phase-Lag Index, WPLI）、部分MI(Partial Mutual Information, PMI)等。而有些功能连接指标的计算原理笔者也并不是十分了解，在这里就不展开介绍，以免误人子弟。如果想对各种各样的功能连接指标有一个系统的了解，笔者推荐HERMES工具包。HERMES是由西班牙马德里技术大学（Technical University of Madrid）的Centre for Biomedical Technology团队研发的基于Matlab的开源EEG工具包，其主要的功能和特点是计算基于各种方法的功能连接，HERMES官方网址：http://hermes.ctb.upm.es/