这里写目录标题
一、线性方程组
1.1 线性方程组
- 线性方程:
- 线性方程组:
- 一组解、解集:
- 例子:求包含两个未知数的两个方程组成的方程组的解,等价于求两条直线的交点:一个数对(a,b)同时满足两个方程,代表这个点同时在两个方程表示的直线上,故而为两直线的交点。同理三个未知数的方程代表面,满足方程组的解集为不同面的交集。
线性方程组的解情况
线性方程组是相容的:一个或无穷个解
不相容:无解
- 解法:两个线性方程组的增广矩阵是行等价的,则它们具有相同的解集
1.2 行化简和阶梯型矩阵
- 先导元素、阶梯型矩阵(3点)和简化阶梯型矩阵(5点):一行中最左边不为0的元素
- 解的存在性问题
定理1 :每个矩阵等价于唯一的简化阶梯型矩阵
- 主元位置和主元列:矩阵A对应的阶梯型矩阵先导元素的位置;主元列是A的含有主元位置的列
- 行化简方法:
- 基本变量、自由变量:化简后的增广矩阵对应一个线性方程组,对应于主元列的变量为基本变量,其他变量为自由变量

定理2(存在与唯一性定理):线性方程组相容(有解)的充要条件是增广矩阵的最右列不是主元列。就是说增广矩阵的阶梯型没有形状如 [0 0 0 0 b] 的行。(b≠0)
唯一性:没有自由变量时,有唯一解,有自由变量时,有无穷个解。
1.3 向量方程
-
向量和向量的代数性质
-
向量的线性组合:

-
若v1,v2,…,vp 是Rn中的向量,则v1,v2,…,vp 所有的线性组合组成的集合用 Span{v1,v2,…,vp}表示,称v1,v2,…,vp 生成(或张成)Rn的子集。就是说Span{v1,v2,…,vp}是所有形如 c1v1 + c2v2 + … +cpvp 的向量的集合
-
要判断向量 b 是否在Span{v1,v2,…,vp} 中,等价判断 向量方程是否有解,等价判断增广矩阵是否有解
-
Span{v} 和Span{u v}的几何解释:在R2中和R3中,注意都是过原点的
1.4 矩阵方程Ax = b


- 方程 Ax = b 有解 放且仅当 b 是 A 各列的线性组合
定理4:设A是 m×n 的矩阵,下列表述等价(注意,讨论的是系数矩阵A),这是讨论对任意b 都可以写成A的各列线性组合
a、对Rm中的每个b,方程 Ax = b 有解
b、Rm 中的每个b 都是A的列的一个线性组合
c、A 的各列生成Rm(Rm中的每一个 向量b都是A的列的线性组合)
d、A 在每一行都有一个主元位置,即增广矩阵的阶梯型没有如 [ 0 0 0 1] 的行
1.5 线性方程的解集
- 齐次线性方程组:形如 Ax = 0,A 是m×n 矩阵,0是Rm中的零向量
齐次方程至少有一个解,即x = 0,称为平凡解
非平凡解(非零向量x):当且仅当方程组至少有一个自由变量
- 参数向量形式:
- 非齐次方程组的解:
定理6:设方程 A x = b 对某个b是相容的,p为一个特解,则方程的解集是 p+ v,其中v是Ax=0的任意一个解。
1.6 应用
1.7 线性无关
- 线性无关

- 矩阵各列线性无关:将上述向量方程写成矩阵形式,矩阵的各列线性无关,当且仅当方程 Ax = 0 仅有平凡解
- 两个向量的集合判断线性相关:是否成倍数关系
- 多个向量的集合:当且至少有一个向量是其他的线性组合,则这个集合是线性相关的
- 若一个向量组的向量的个数超过了向量中元素的个数,则这个向量组是线性相关的。
- 若向量组中包含零向量,则他们线性相关

二 、矩阵代数
2.1 矩阵运算(√)
- 矩阵的和 、标量乘法
- 矩阵的乘法
- 矩阵的乘幂
- 矩阵的转置:若干个矩阵的乘积的转置 等于 转置的乘积,但是顺序相反
2.2 矩阵的逆

定理4 :矩阵可逆,当且仅当行列式 不为 0
定理5:若A是n x n可逆矩阵,则对于Rn中任意b,方程Ax = b 有唯一解 ,x = A(-1)b
定理6:乘积的逆 等于 相反顺序 逆的乘积
- 通过行变换求逆

2.4 分块矩阵
2.5 矩阵的因式分解
2.8 Rn的子空间
Rn的一个子空间是 Rn中的集合 H, 它具有以下三个性质:1、零向量属于H 。2、对H中的任意两个向量 u和v,u+v属于H 。3、对H中的任意向量u,数乘 cu属于H
即子空间对于加法和标量乘法是封闭的
- 例子:通过原点的平面;通过原点的直线;不过原点的不是子空间

- 矩阵的列空间:矩阵A的各列的线性组合 的 集合,记作Col A
A 的列空间是所有使方程 Ax = b 有解的 向量b的集合
- 矩阵的零空间:是齐次方程 Ax = 0 的所有解的集合,记作 Nul A
2.9 维数与秩
- 坐标系:
 - 子空间的维数:非零子空间H的维数,用dim H表示,是H的任意一个基 的向量的 个数,零子空间的维数定义为零;
- 子空间的维数:非零子空间H的维数,用dim H表示,是H的任意一个基 的向量的 个数,零子空间的维数定义为零; - 例子:Rn空间的维数是 n,Rn的每个基由 n个向量组成;R3中的一个经过原点的平面维数是2,一条经过原点的直线维数是1。
Nul A 的维数,是求出 Ax = 0中自由变量的个数
矩阵A的秩(rank A)定义为 A列空间的维数;A的主元列形成Col A的一个基,A的秩正好是A 的主元列的个数。
定理14(秩定理):结合上面两条,若矩阵A由n列,则rank A + dim (Nul A)= n;
定理15(基定理)
三、行列式
3.1 行列式介绍
- 行列式的计算法则
定理2:若A为三角矩阵,则det A等于A的对角线上元素乘积
3.2 行列式性质
dingl
定理4:方阵A是可逆的,当且仅当 detA 不为0
定理
定理5:
3.3 克拉默法则、体积和线性变换
四、向量空间
4.1 向量空间 与 子空间


每个子空间都是一个向量空间,典型的为 R3空间中的一个过原点的平面,或者R3中一个过原点的直线;或者R2中一个过原点的直线;

4.2 零空间、列空间和线性变换
- 矩阵的零空间


定理2:
- 矩阵的列空间



- 线性变换的核 与 值域

4.3 线性无关集和基
五、特征值与特征向量
5.1 特征向量与特征值
- 定义:矩阵A 是n×n矩阵看,x为非零向量,若存在数 a 使得 Ax = ax, 则称a为A的特征值,x称为对应于 a 的特征向量。(被A变换成自身一个数量倍数的向量。
- 特征值是 使方程(A-aI)x=0 有非平凡解的值,有自由变量的值,就是特征值。
- 应该是 先求特征值,然后求特征值对应的特征向量,某个特种值对应的特种向量不唯一;是一个集合,称为矩阵A对应于特征值a的特征空间;
- 矩阵A对特征空间具有扩张作用;是指给定某个特征值后,可以确定一个特种空间,矩阵A乘上这个特征空间里的任何向量,都等于这个向量乘特征值
定理1:三角矩阵的主对角线的元素是特征值
定理2:
5.2 特征方程
六、正交性和最小二乘
6.1 内积、长度和正交性
- 内积(点积):u 和 v 是 Rn 中 n×1 向量,内积u转置乘v,为一标量
- 性质:交换 、数乘、分配
- 向量的长度(范数):
- 向量间距离:
- 正交向量:两个向量的内积是0,则他们是正交的;几何上表示为u到v的距离和u到-v的距离相等;
定理2(勾股定理)
6.2 正交集


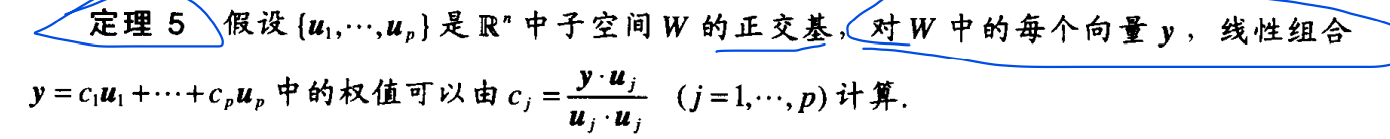
-
正交投影:

-
正交投影是定理5的特殊形式,将Rn中的向量分解为两个相互垂直的向量,这两个相互垂直的向量就是 一组正交基,即由两个向量组成的正交基;因为相互垂直就是正交集,正交集就是正交基















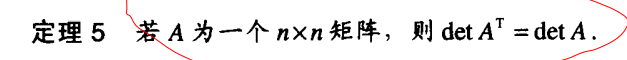





















 2723
2723











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








