Python实现ACO蚁群优化算法优化支持向量机回归模型(SVR算法)项目实战

说明：这是一个机器学习实战项目（附带数据+代码+文档+视频讲解），如需数据+代码+文档+视频讲解可以直接到文章最后获取。

1.项目背景

蚁群优化算法(Ant Colony Optimization, ACO)是一种源于大自然生物世界的新的仿生进化算法，由意大利学者M. Dorigo, V. Maniezzo和A.Colorni等人于20世纪90年代初期通过模拟自然界中蚂蚁集体寻径行为而提出的一种基于种群的启发式随机搜索算法"。蚂蚁有能力在没有任何提示的情形下找到从巢穴到食物源的最短路径，并且能随环境的变化，适应性地搜索新的路径，产生新的选择。其根本原因是蚂蚁在寻找食物时，能在其走过的路径上释放一种特殊的分泌物——信息素(也称外激素)，随着时间的推移该物质会逐渐挥发，后来的蚂蚁选择该路径的概率与当时这条路径上信息素的强度成正比。当一条路径上通过的蚂蚁越来越多时，其留下的信息素也越来越多，后来蚂蚁选择该路径的概率也就越高，从而更增加了该路径上的信息素强度。而强度大的信息素会吸引更多的蚂蚁，从而形成一种正反馈机制。通过这种正反馈机制，蚂蚁最终可以发现最短路径。

本项目通过ACO蚁群优化算法优化支持向量机回归模型。

2.数据获取

本次建模数据来源于网络(本项目撰写人整理而成)，数据项统计如下：

 数据详情如下(部分展示)：

3.数据预处理

3.1 用Pandas工具查看数据

使用Pandas工具的head()方法查看前五行数据：

 关键代码：

3.2数据缺失查看

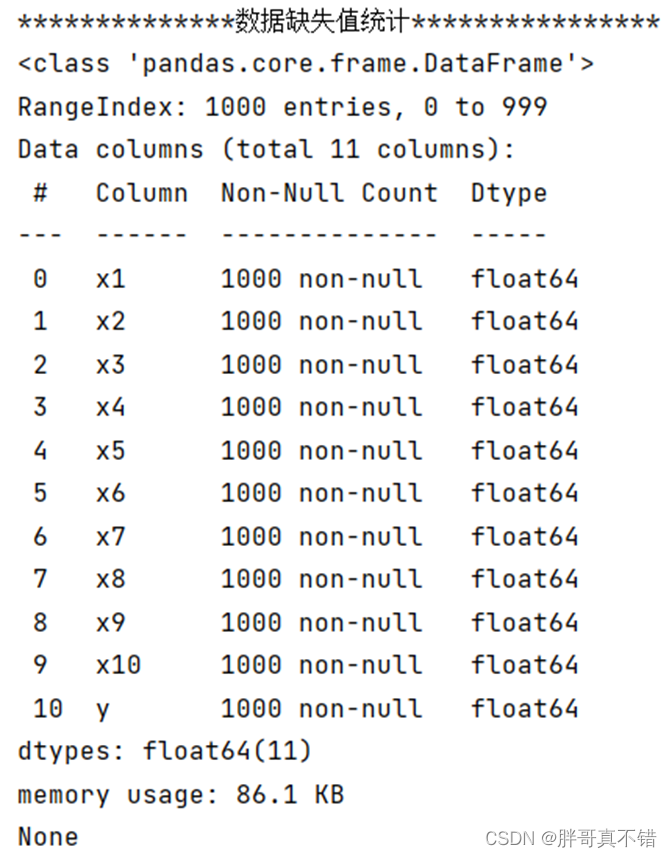
使用Pandas工具的info()方法查看数据信息：

从上图可以看到，总共有11个变量，数据中无缺失值，共1000条数据。

关键代码：

3.3数据描述性统计

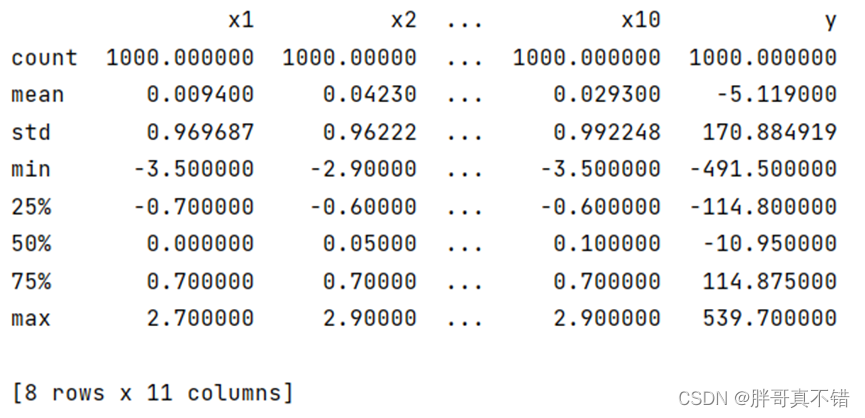
通过Pandas工具的describe()方法来查看数据的平均值、标准差、最小值、分位数、最大值。

 关键代码如下：

4.探索性数据分析

4.1 y变量分布直方图

用Matplotlib工具的hist()方法绘制直方图：

 4.2 相关性分析

5.特征工程

5.1 建立特征数据和标签数据

关键代码如下：

5.2 数据集拆分

通过train_test_split()方法按照80%训练集、20%测试集进行划分，关键代码如下：

6.构建ACO蚁群优化算法优化支持向量机回归模型

主要使用ACO蚁群优化算法优化SVR算法，用于目标回归。

6.1 算法介绍

     说明：ACO算法介绍来源于网络，供参考,需要更多算法原理，请自行查找资料。

蚁群算法是对自然界蚂蚁的寻径方式进行模拟而得出的一种仿生算法。蚂蚁在运动过程中，能够在它所经过的路径上留下信息素进行信息传递，而且蚂蚁在运动过程中能够感知这种物质，并以此来指导自己的运动方向。因此，由大量蚂蚁组成的蚁群的集体行为便表现出一种信息正反馈现象:某一路径上走过的蚂蚁越多，则后来者选择该路径的概率就越大。

 

蚁群算法公式:

 

蚁群算法程序概括:

(1)参数初始化

在寻最短路钱，需对程序各个参数进行初始化，蚁群规模m、信息素重要程度因子α、启发函数重要程度因子β、信息素会发因子、最大迭代次数ddcs_max，初始迭代值为ddcs=1。

(2)构建解空间

将每只蚂蚁随机放置在不同的出发地点，对蚂蚁访问行为按照公式计算下一个访问的地点，直到所有蚂蚁访问完所有地点。

(3)更新信息素

计算每只蚂蚁经过的路径总长Lk,记录当前循环中的最优路径，同时根据公式对各个地点间连接路径上的信息素浓度进行更新。

(4)判断终止

迭代次数达到最大值前，清空蚂蚁经过的记录，并返回步骤2。

6.2 ACO蚁群优化算法寻找最优参数值

关键代码：

 适应度迭代曲线图：

 最优参数：

 6.3 最优参数值构建模型

7.模型评估

7.1评估指标及结果

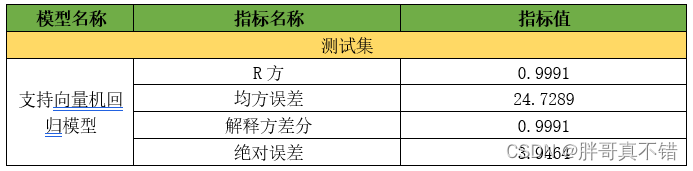
评估指标主要包括R方、均方误差、解释性方差、绝对误差等等。

 从上表可以看出，R方分值为0.9991，说明模型效果比较好。

关键代码如下： 

7.2 真实值与预测值对比图

 从上图可以看出真实值和预测值波动基本一致，模型效果良好。

8.结论与展望

综上所述，本文采用了ACO蚁群优化算法寻找支持向量机SVR算法的最优参数值来构建回归模型，最终证明了我们提出的模型效果良好。此模型可用于日常产品的预测。

# 本次机器学习项目实战所需的资料，项目资源如下：
 
# 项目说明：

# 链接：https://pan.baidu.com/s/18MvTpXBDipoThv8ODoDd9w 
# 提取码：8kzs

# 查看数据前5行
print('*************查看数据前5行*****************')
print(df.head())

# 数据缺失值统计
print('**************数据缺失值统计****************')
print(df.info())

# 描述性统计分析
print(df.describe())
print('******************************')

# y变量分布直方图
fig = plt.figure(figsize=(8, 5))  # 设置画布大小
plt.rcParams['font.sans-serif'] = 'SimHei'  # 设置中文显示
plt.rcParams['axes.unicode_minus'] = False  # 解决保存图像是负号'-'显示为方块的问题
data_tmp = df['y']  # 过滤出y变量的样本
# 绘制直方图  bins：控制直方图中的区间个数 auto为自动填充个数  color：指定柱子的填充色
plt.hist(data_tmp, bins='auto', color='g')
plt.xlabel('y')
plt.ylabel('数量')
plt.title('y变量分布直方图')
plt.show()