基于线性回归房价预测散点图和折线图

	回归是统计学中最有力的工具之一。机器学习监督学习算法分为分类算法和回归算法两 种，其实就是根据类别标签分布类型为离散型、连续性而定义的。回归算法用于连续型分布 预测，针对的是数值型的样本，使用回归，可以在给定输入的时候预测出一个数值，这是对 分类方法的提升，因为这样可以预测连续型数据而不仅仅是离散的类别标签。 回归分析中，只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示， 这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量，且因 变量和自变量之间是线性关系，则称为多元线性回归分析。
	多元线性回归
	假定预测值与样本特征间的函数关系是线性的，回归分析的任务，就在于依据样本 X 和 Y 的观察值。去预计函数 h，寻求变量之间近似的函数关系。定义：
![在这里插入图片描述](https://img-blog.csdnimg.cn/20190929143207727.png)
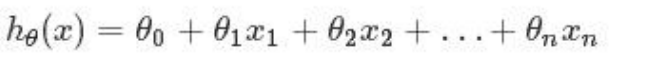
	当中，n=特征数目； xj=每一个训练样本第 j 个特征的值，能够觉得是特征向量中的第 j 个值。 为了方便。记 x0=1。则多变量线性回归能够记为：
	![在这里插入图片描述](https://img-blog.csdnimg.cn/20190929143247633.png)

#-*-coding:utf-8-*-
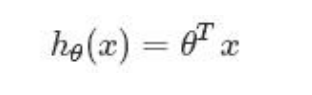
import   pandas  as  pd
import   numpy  as  np
import   matplotlib.pyplot  as  plt
#加载数据
from  sklearn.datasets  import  load_boston
from  sklearn.model_selection  import train_test_split
from  sklearn.preprocessing  import  StandardScaler
from   sklearn.linear_model  import LinearRegression#正规方程求解的线性回归
from  sklearn.linear_model  import SGDRegressor#sgd线性回归，随机梯度下降线性回归
from  sklearn.linear_model  import Ridge#岭回归算法
#默认不支持中文,需要配置RC参数
plt.rcParams['font.sans-serif']='SimHei'
#设置字体之后不支持,需要去设置RC参数更改编码
plt.rcParams['axes.unicode_minus']=False
def  show_res(</