Graph Neural Network-Based Anomaly Detection in Multivariate Time Series 综述

原文链接：https://arxiv.org/abs/2106.06947
代码链接：GitHub - d-ailin/GDN: Implementation code for the paper "Graph Neural Network-Based Anomaly Detection in Multivariate Time Series"

简述：提出一种图偏差网络(GDN)，旨在以图的形式学习传感器之间的关系，然后识别和解释学习模式的偏差。首先将传感器看作节点，计算其嵌入向量，利用点积即求取cos距离的方式得到节点嵌入向量之间的相似度，以此来评判传感器之间是否存在边链接，以此构建邻接矩阵。其次，引入注意力机制以及特征提取的方式去求取t时刻的模型预测s(t) (N*1维度)，并需要利用预测的s(t)和实际测量值s^(t)的均方误差作为最小化损失的函数；最后为了检测异常，我们使用超过验证数据集的最大异常评分来设置阈值。在测试期间，任何异常得分超过阈值的时间点都将被视为异常。测试方式如下，假如某类故障发生，1号传感器难以检测（即发生故障时，1号传感器的预测的波形变化幅度与实际正常阈值相比并不明显），但由于图网络的联系性，1号传感器的变化会间接影响2号传感器的波形变化，若2号传感器是最大异常点，2号传感器的预测变化明显地高于阈值（即使2号传感器实际并没有故障），因此，可以从2号传感器的变化反推回1号传感器的故障。

摘要：

最近，深度学习方法使高维数据集异常检测的改进成为可能。然而，现有的方法并没有明确地学习变量之间现有关系的结构，也没有利用它们来预测时间序列的预期行为。我们的方法结合了结构学习方法和图神经网络，另外使用注意力权重为检测到的异常提供可解释性。

1.引文

随着传感器数据的复杂性和维度的增长，人类越来越无法手动监控这些数据。这需要自动异常检测方法，可以快速检测高维数据中的异常，并向人类操作员解释这些异常，允许他们尽可能快地诊断和响应异常。
由于在历史数据中固有的缺乏标记异常，以及异常的不可预测和高度变化的性质，异常检测问题通常被视为无监督学习问题。(Due to the inherent lack of labeled anomalies in historical data, and the unpredictable and highly varied nature of anomalies, the anomaly detection problem is typically treated as an unsupervised learning problem.)
然而，非深度学习方法通常以相对简单的方式对传感器之间的相互关系进行建模:例如，仅捕捉线性关系，这对于许多现实世界中复杂的高度非线性关系是不够的。
最近，基于深度学习的技术使高维数据集异常检测的改进成为可能。例如，自动编码器(AE) (Aggarwal 2015)是一种常用的异常检测方法，它使用重构误差作为异常值评分。最近，生成对抗网络(GANs) (Li et al. 2019)和基于lstm的方法(Qin et al. 2017)也报道了在多元异常检测方面有很好的性能。然而，大多数方法没有明确地了解哪些传感器是相互关联的，因此在建立具有许多潜在相互关系的传感器数据时，面临许多困难。这限制了他们在异常事件发生时检测和解释偏离这种关系的能力。
然而，将GNNs应用于时间序列异常检测需要克服两个主要挑战。首先，不同的传感器有非常不同的性能:例如，一个可以测量水压，而另一个可以测量流量。然而，传统的GNN使用相同的模型参数来建模每个节点的行为。其次，在我们的设置中，图的边(即传感器之间的关系)最初是未知的，需要利用我们的模型进行学习。
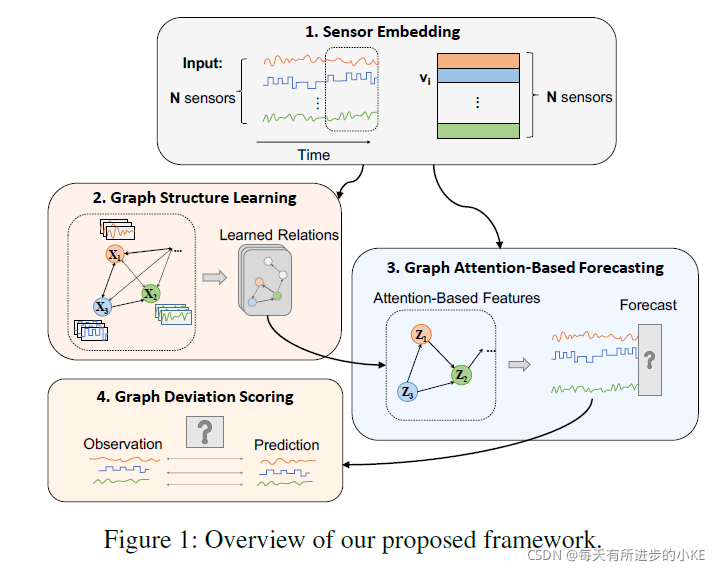
因此，在这项工作中，我们提出了新的图偏差网络(Graph Deviation Network, GDN)方法，它学习传感器之间的关系图，并检测与这些模式（pattern）的偏差。我们的方法包括四个主要部分:
1.Sensor Embedding:利用嵌入向量灵活地捕捉每个传感器的独特特征
2.Graph Structure Learning:学习传感器之间的关系，并把它们视作图边
3. Graph Attention-Based Forecasting:根据图中邻近传感器的注意力函数，预测传感器未来的行为
4. Graph Deviation Scoring:图偏差评分识别并解释图中所学习的传感器关系的偏差。
简而言之，我们的工作贡献点包括：

• 提出GDN,一种基于注意力的图神经网络，以此去学习传感器之间的关系依赖图，并识别和解释这些关系的偏差
• 我们在两个水处理厂的真实异常数据集上进行了实验。我们的结果表明，GDN检测异常比基线方法更准确。
• 我们通过案例研究表明，GDN通过其嵌入和学习图提供了一个可解释的模型。我们表明，基于检测到偏差的子图、注意力权重，并通过比较这些传感器上的预测和实际行为，它有助于解释异常。

2.相关工作

异常检测的目的是检测偏离大部分数据的异常样本
多变量时间序列建模：通常基于多变量时间序列过去的行为建模。为了学习非线性高维时间序列的表示和预测时间序列数据，基于深度学习的时间序列方法引起了人们的兴趣，然而，现有深度学习方法没有明确地学习不同时间序列之间的关系，这对异常检测是有意义的:例如，它们可以通过识别这些关系的偏差来诊断异常。
基于图的方法通过边表示传感器之间的相互依赖关系，为传感器之间的关系建模提供了一种方法。然而，这些方法使用相同的模型参数来建模每个节点的行为，因此在表示不同传感器的非常不同的行为方面面临限制。此外，GNN通常需要图结构作为输入，而在我们的设置中，图结构最初是未知的，需要从数据中学习。

3.所提方法

3.1 问题描述 

训练数据（Ttrian个采样时间单位，N个传感器）：
在每个时间点t，N维向量，表示我们的N个传感器的值。
目标是从Ttest个分离时间单位的测试数据中检测异常
测试的输出结果是，“1”表示异常

3.2  概述

我们的GDN方法旨在以图的形式学习传感器之间的关系，然后识别和解释学习模式的偏差。它包括引文所提及的四个主要部分。

3.3 传感器嵌入

在许多传感器数据设置中，不同的传感器可以有非常不同的特性，而这些特性可以以复杂的方式联系起来。例如，假设我们有两个水箱，每个水箱都有一个传感器测量水箱中的水位，还有一个传感器测量水箱中的水质。那么，两个水位传感器的行为可能会相似，两个水质传感器的行为也可能相似。然而，同样有可能的是，同一水箱内的传感器会显示出很强的相关性。因此，理想情况下，我们希望以一种灵活的方式表示每个传感器，以多维方式捕捉其行为背后的不同因素。

 这些嵌入是随机初始化的，然后和模型的其余部分一起训练。这些嵌入之间的相似性vi表示行为的相似性，因此，具有相似嵌入值的传感器之间应该有较高的相关性。(可以把d看作是提取传感器的d个特征，根据这些特征来评判传感器数据的波形相似性，以此来确立传感器数据的相关性)
在我们的模型中，这些嵌入将以两种方式使用:1)用于结构学习，以确定哪些传感器彼此相关，2)在我们的注意机制中，以一种允许不同类型的传感器产生异质效应（heterogeneous effects）的方式对邻居进行注意。

3.4 图结构学习

我们框架的一个主要目标是以图形结构的形式来学习传感器之间的关系。为此，我们将使用一个有向图，其节点表示传感器，其边表示传感器之间的依赖关系。从一个传感器到另一个传感器的边缘表明第一个传感器用于模拟第二个传感器的行为。我们使用有向图是因为传感器之间的依赖模式不需要是对称的。我们用邻接矩阵A来表示这个有向图。
我们设计一个灵活的框架,它可以应用到1)通常情况下我们没有之前的图结构的信息,2)我们有一些先验信息,边缘是合理的(如最小交互性的传感器系统可以分成不同部分)。
这种先验信息可以灵活地表示为每个传感器i的一组候选关系Ci：

 为了选择传感器i在候选节点之间的依赖关系，我们计算节点i的嵌入向量与其候选节点之间的相似度：

即首先计算传感器i的嵌入向量与候选关系之间的归一化点积。然后，我们选择这种归一化点积的前k个值:这里TopK表示其输入(即归一化点积)中前k个值的节点索引。k的值可以由用户根据所需的稀疏程度选择。接下来，我们将定义我们的基于注意力的图模型，它利用这个学习到的邻接矩阵A。

 3.5 基于图注意力网络预测

为了对异常进行有效的解释，我们的模型需要解决的是：

• 哪些传感器偏离了正常行为？
• 传感器在哪些方式偏离了正常行为？

为了实现这些目标，我们使用了一种基于预测的方法，即我们基于过去预测每个传感器每次的预期行为。这使得用户能够很容易地识别与预期行为有很大偏差的传感器。此外，用户可以比较每个传感器的预期和观测行为，以理解为什么模型认为一个传感器是异常的。
因此，在时间t时，我们根据大小为w的滑动窗口对历史时间序列数据(无论是训练数据还是测试数据)定义我们的模型输入:

 我们的模型需要预测的目标输出是当前时刻的传感器数据，即

特征提取 为了捕获传感器之间的关系，我们引入了一种基于图注意的特征提取器，以学习到的图结构为基础，将节点的信息与其相邻节点进行融合。不同于现有的图注意机制，我们的特征提取器包含了传感器嵌入向量，它描述了不同类型传感器的不同行为。为此，我们计算节点i的聚合表示zi，如下所示：

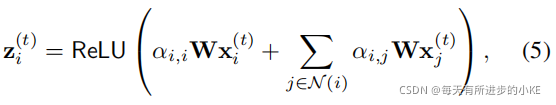
 其中为节点i的输入特征，为由学习邻接矩阵A得到的节点i的邻居集合，为可训练权矩阵，对每个节点进行共享线性变换，注意系数计算为：

 表示串联;因此，将传感器嵌入与相应变换后的特征连接起来，a是注意机制学习系数的向量。我们使用LeakyReLU作为非线性激活来计算注意系数，并使用Eq.(8)中的softmax函数对注意系数进行归一化。

输出层 通过上述特征提取器，我们得到了所有N个节点的表示，即。对于每个)，将它与相应的时间序列嵌入vi按元素相乘(表示），并将所有节点计算的堆叠结果作为全连接层的输入，输出的维度为N，从而预测时间t矢量传感器的值，即：

模型的预测输出用s(t)表示。我们使用预测输出s(t)和观测数据s^(t)之间的均方误差作为最小化损失的函数:

3.6 图偏差得分

鉴于习得的关系，我们想要检测和解释偏离这些关系的异常。为了做到这一点，我们的模型为每个传感器计算个别的异常分数，并将它们合并为每个时间点的单个异常分数，从而允许用户定位哪些传感器是异常的，正如我们将在我们的实验中显示的那样。
异常评分将t时刻的预期行为与观测到的行为(实际行为)进行比较，计算出t时刻的传感器i的错误值Err：

 由于不同的传感器可能具有非常不同的特性，它们的偏差值也可能具有非常不同的尺度。为了防止任何一个传感器产生的偏差超过其他传感器，我们对每个传感器的误差值进行了稳健的归一化：

 分别是值在时间间隔内的中位数和四分位距IQR (IQR：被定义为一个分布或一组值的第1个和第3个四分位数之间的差值，是对分布的扩展的可靠度量，常用于识别异常值)。
然后，为了计算时间点t的总体异常，我们使用max函数对传感器进行聚合(我们使用max是因为异常只影响一小部分传感器，甚至单个传感器):

 为了抑制值的突变往往不能完美地预测，并导致误差值的尖峰，即使这种行为是正常的。类似于(Hundman等人。2018b)，我们使用简单移动平均(simple moving average，SMA)来生成平滑的分数。最后，如果超过固定阈值，则将时间标记为异常。虽然可以使用不同的方法来设置阈值，如极值理论(Siffer et al. 2017)，但为了避免引入额外的超参数，我们在实验中使用了一种简单的方法，即设置阈值为相对于验证数据的最大值。

4.实验

 从准确率，模型各部分贡献度，模型可解释性和异常定位去评判模型

4.1 数据

  

来自水处理厂的两个数据集：SWat 和 WADI, 包括真实异常数据，会在不同的时间间隔内进行一些受控的物理攻击，这与测试集中的异常情况相对应
 通过取中值对原始数据样本进行下采样，每10秒进行一次测量。结果标签是10秒内最常见的标签。由于系统在第一次启动时需要5-6小时才能达到稳定(Goh et al. 2016)，我们消除了两个数据集的前2160个样本。
为了检测异常，我们使用超过验证数据集的最大异常评分来设置阈值。在测试时间，任何异常得分超过阈值的时间点都将被视为异常。

4.2 组件功能

为了研究我们方法中每个组件的必要性，我们逐步排除组件，观察模型性能是如何下降的。首先，我们研究了学习图的重要性，将其替换为一个静态完整图，其中每个节点连接到所有其他节点。其次，为了研究传感器嵌入的重要性，我们使用了一个没有传感器嵌入的注意机制:即。最后，我们禁用了注意机制，而是使用分配给所有邻点的相同权重进行聚合。结果汇总在表3中，并提供以下结果：

• 图结构学习器提高了性能，特别是对于大规模数据集。
• 从注意机制中移除传感器嵌入的变体在两个数据集中的性能都不如原始模型。这意味着嵌入特征改善了图注意机制中权重系数的学习。
• 在我们的实验中，去除注意机制对模型性能的影响最大。由于传感器有非常不同的行为，平等地对待所有邻居会引入噪声并误导模型。这验证了图形注意机制的重要性

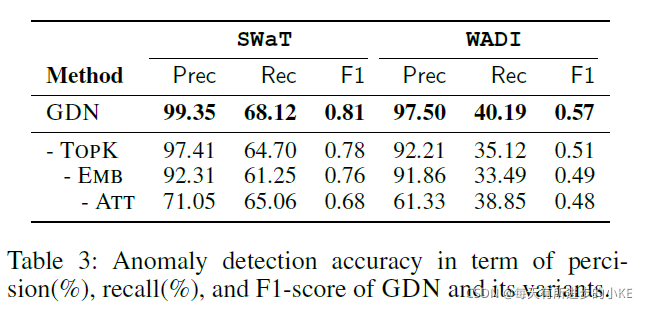
 这些发现表明，GDN使用的学习图结构、传感器嵌入和注意机制都有助于其准确性，这为其优于基线方法提供了解释。

 4.3 模型的可解释性

通过传感器嵌入的可解释性

为了解释学习的模型，我们可以可视化其传感器嵌入向量，例如使用t-SNE(Maaten and Hinton 2008)，如图2中的WADI数据集所示。这个嵌入空间的相似性表明传感器行为之间的相似性，因此检查这个图允许用户推断行为相似的传感器组。

 

 为了验证这一点，我们在WADI系统中使用对应于7类传感器的7种颜色对节点进行着色。该表示在投影的二维空间中表现出局部聚类，验证了学习的特征表示在反映局部传感器行为相似度方面的有效性。此外，我们观察到一组传感器形成一个局部星团，显示在虚线圈区域。通过查看数据，我们发现这些传感器测量的是在WADI配水网络中执行类似功能的水箱中的类似指标，这说明了这些传感器之间的相似性。

图边和注意力权重的可解释性

 在我们学习的图中，边通过指示哪些传感器彼此相关而提供了可解释性。此外，注意权重进一步表明了每个节点的邻点在建模节点行为中的重要性。
图3(左)显示了WADI数据集上学习的这个图的示例。下面的小节进一步展示了一个使用此图定位和理解异常的案例研究。

4.4 异常定位

图3(左)显示了传感器的学习图，边通过它们的注意力权重进行加权，并使用force-directed布局绘制(Kobourov 2012)。

 我们进行了一个案例研究，涉及一个已知原因的异常:正如WADI数据集文档中记录的那样，这个异常是由一个流量传感器1_FIT_001_PV通过错误读数造成的。这些错误读数在传感器的正常范围内，所以检测这种异常是不容易的。
在此攻击期间，GDN进行识别1_MV_001_STATUS作为异常评分最高的偏差传感器，如图3左边的三角形标识，该传感器的较大偏差表明1_MV_001_STATUS可能是被攻击传感器，或者与被攻击传感器密切相关。
“GDN”(红色圈表示)为偏离传感器关注权重最高的传感器。事实上，这些邻居是密切相关的传感器:1_FIT_001_PV作为邻点，通常与1_MV_001_STATUS高度相关，因为后者显示阀门的状态，该阀门控制由前者测量的流量。然而，攻击导致偏离了这一关系，因为攻击只导致1_FIT_001_PV的虚假读数。  
GDN进一步通过比较图3(右)中预测和观测的传感器值来理解这种异常:对于1_MV_001_STATUS，我们的模型预测了增加(随着1_FIT_001_PV增加，我们的模型已经知道传感器一起增加)。但是即使受到攻击，然而1_MV_001_STATUS没有变化，导致GDN检测到较大的错误为异常。
综上所述:1)模型的个体异常评分有助于定位异常;2)它的注意力权重有助于找到密切相关的传感器;3)它对每个传感器预期行为的预测使我们了解异常是如何偏离预期的。

5.结论

在这项工作中，我们提出了我们的图偏差网络(GDN)方法，该方法学习传感器之间的关系图，并检测这些模式的偏差，同时结合传感器嵌入。在两个真实传感器数据集上的实验表明，GDN在准确性上优于基线，提供了一个可解释的模型，并帮助用户定位和理解异常。未来的工作可以考虑增加体系结构和在线训练方法，以进一步提高方法的实用性。