机器学习之贝叶斯分类器——《机器学习》周志华著

1. 解释先验概率、后验概率、全概率公式、条件概率公式，结合实例说明贝叶斯公式，如何理解贝叶斯定理？

i) 先验概率：

用$P(h)$表示在没有训练数据前假设$h$拥有的初始概率。$P(h)$被称为$h$的先验概率。先验概率反映了关于$h$是一正确假设的机会的背景知识如果没有这一先验知识，可以简单地将每一候选假设赋予相同的先验概率。

ii) 后验概率：

$P(D)$表示训练数据$D$的先验概率，$P(D|h)$表示假设$h$成立时$D$的概率。机器学习中，我们关心的是$P(h|D)$，即给定$D$时$h$的成立的概率，称为$h$的后验概率。

iii) 全概率概率：

1. 如果事件组$B_1$，$B_2$，…满足
   1)$B_1$，$B_2$…两两互斥，即$B_i\cap B_j=\varnothing$， $i,j=1，2，....，i,j=1，2，....，$且$P(B_i)>0,i=1,2,....$;
   2)$B_1\cup B_2\cup ...=\Omega$，称事件组$B_1$,$B_2$,…是样本空间$\Omega$的一个划分。
   设$B_1$,$B_2$,…是样本空间$\Omega$的一个划分，$A$为任一事件，则：
   

iv) 条件概率：

一个事件发生后另一个事件发生的概率。一般的形式为$P(x|y)$表示$y$发生的条件下$x$发生的概率。

v) 贝叶斯公式

与全概率公式解决的问题相反，贝叶斯公式是建立在条件概率的基础上寻找事件发生的原因（即大事件$A$已经发生的条件下，分割中的小事件$B_i$的概率），设$B_1$,$B_2$,…是样本空间$\Omega$的一个划分，则对任一事件$A$$(P(A)>0)$,有

上式即为贝叶斯公式$(Bayesformula)$，$B_i$常被视为导致试验结果$A$发生的”原因“，$P(B_i)(i=1,2,...)$表示各种原因发生的可能性大小.

• 实例
  小张从家到公司上班总共有三条路可以直达（如下图），但是每条路每天拥堵的可能性不太一样，由于路的远近不同，选择每条路的概率如下
  
  每天上述三条路不拥堵的概率分别为：
  
  假设遇到拥堵会迟到，到达公司未迟到选择第１条路的概率是多少？
  
  
  
  
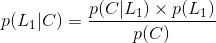
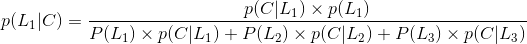
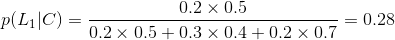
  所以选择第一条的概率是0.28。

2. 结合实例说明朴素贝叶斯分类器是如何对测试样本进行分类的？并归纳总结算法步骤。

我们设一个待分类项$X=f_1{f}_2,\cdots ,f_n$，其中每个$f$为$X$的一个特征属性，然后设一个类别集合$C_1,C_2,\cdots ,C_m$。

然后需要计算$P(C_1|X),P(C_2|X),\cdots ,P(C_m|X)$，我们可以根据一个训练样本集合（已知分类的待分类项集合），然后统计得到在各类别下各个特征属性的条件概率：
$P(f_1|C_1),P(f_2|C_1),\cdots ,P(f_n|C_1),\cdots ,P(f_1|C_2),P(f_2|C_2),\cdots ,P(f_n{C}_2),\cdots ,P(f_1|C_m),P(f_2|C_m),\cdots ,P(f_n|C_m)$

如果$P(C_k|X)=MAX(P(C_1|X),P(C_2|X),\cdots ,P(C_m|X))$，则$X\in C_k$

朴素贝叶斯会假设每个特征都是独立的，根据贝叶斯定理可推得：$P(C_i|X)=P(X|C_i)P(C_i)P(X)$，由于分母对于所有类别为常数，因此只需要将分子最大化即可，又因为各特征是互相独立的，所以最终推得：

• 实例

现有一网站想要通过程序自动识别出账号的真实性（将账号分类为真实账号与不真实账号，所谓不真实账号即带有虚假信息或恶意注册的小号）。
首先需要确定特征属性和类别，然后获取训练样本。假设一个账号具有三个特征：日志数量/注册天数（$F_1$）、好友数量/注册天数（$F_2$）、是否使用了真实的头像（True为1，False为0）。
该网站使用曾经人工检测过的10000个账号作为训练样本，那么计算每个类别的概率为：
$P\left(C_0\right)=8900÷10000=0.89,P\left(C_1\right)=1100÷10000=0.11$,$C_0$为真实账号的类别概率也就是89%，$C_1$为虚假账号的类别概率也就是11%。
之后需要计算每个类别下的各个特征的条件概率，代入朴素贝叶斯分类器，可得$P(F_1|C)P(F_2|C)P(F_3|C)P(C)$，不过有一个问题是，$F_1$与$F_2$是连续变量，不适宜按照某个特定值计算概率。解决方法为将连续值转化为离散值，然后计算区间的概率，比如将$F_1$分解为$[0,0.05]、[0.05,0.2]、[0.2,+\infty ]$三个区间，然后计算每个区间的概率即可。

已知某一账号的数据如下：$F_1=0.1,F_2=0.2,F_3=0$，推测该账号是真实账号还是虚假账号。在此例中，$F_1$为0.1，落在第二个区间内，所以在计算的时候，就使用第二个区间的发生概率。根据训练样本可得出结果为：
接下来使用训练后的分类器可得出该账号的真实账号概率与虚假账号概率，然后取最大概率作为它的类别：


最终结果为该账号是一个真实账号。

3. 分别说明如何用极大似然估计和贝叶斯估计进行朴素贝叶斯的参数估计。

贝叶斯分类器设计时，需要知道先验概率$P\left({\omega }_i\right)$和类概率密度函数$P\left(x\mid {\omega }_i\right)$，然后再按照最小错误率或者最小风险标准进行决策。

但是，在实际的工程应用中，类概率密度函数往往是未可知的。即使把类概率密度函数近似为正态分布函数，其分布的均值和方差也是未知的。

因此，我们需要从已知的有限的样本中，尽可能地估计出类条件概率密度函数的参数，来方便我们设计分类器。换句话说，我们直接从样本出发，已知类概率密度函数的形式，但是类条件概率密度函数的参数未知，依然能够设计出分类器。

根据待分类数据的随机性，可以将这种参数估计的方法分为两类，即最大似然估计和贝叶斯估计。后者认为，待估计参数是完全随机、测不准的。而前者认为参数是固定的。

最大似然估计

已知：样本集 D = { x 1 , x 2 , . . . , x n } D=\left \{ x_{1},x_{2},...,x_{n} \right \} D={x1​,x2​,...,xn​},且每类样本都是从类条件概率密度函数$P(X|{\omega }_{i}c)$的总体中独立抽取出来的。

求解目标：

对目标进行简化：

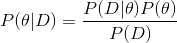
在最大似然估计中，认为$\theta$是确定的，即$P(\theta )$， 是一个常数。而$P(D)$是根据已有的数据得到，也是确定的。因此：

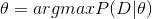
构造函数


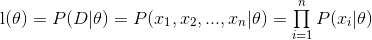
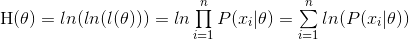
则

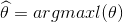
或者

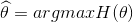
贝叶斯估计与最大似然估计的不同之处在于，不认为$\theta$是确定的常数，而认为$\theta$是随机变量。这样一来：

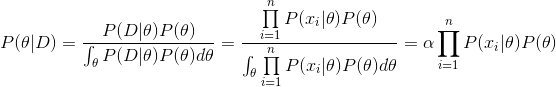
其中$\alpha$是无关量，则

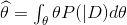
可以看出：

最大似然估计和贝叶斯估计的不同之处在于：

(1) 前者认为待估参数是确定的。而后者认为待估参数是随机的。

(2) 有(1)造成了对目标进行简化时的不同，即对$P(\theta )$的处理方式不同。

(3) 对估计量 的计算方式不同。

4. 编程实现拉普拉斯修正的朴素贝叶斯分类器，并以西瓜数据集3.0为例（P84），对P151的测试样本1进行判别。

朴素贝叶斯的训练过程就是估计类别先验概率以及类条件概率的过程；测试阶段根据训练得到的概率值计算出类别的后验概率并取概率最大的类别作为样本分类。根据数据集3.0得到的拉普拉斯朴素贝叶斯分类器把测试样例预测为正类，即好瓜。
本人认为有两种较好的python3.6编程方法，列出如下：

第一种：

// An highlighted block
import numpy as np
 
D = np.array([
    [1, 1, 1, 1, 1, 1, 0.697, 0.460, 1],
    [2, 1, 2, 1, 1, 1, 0.774, 0.376, 1],
    [2, 1, 1, 1, 1, 1, 0.634, 0.264, 1],
    [1, 1, 2, 1, 1, 1, 0.608, 0.318, 1],
    [3, 1, 1, 1, 1, 1, 0.556, 0.215, 1],
    [1, 2, 1, 1, 2, 2, 0.403, 0.237, 1],
    [2, 2, 1, 2, 2, 2, 0.481, 0.149, 1],
    [2, 2, 1, 1, 2, 1, 0.437, 0.211, 1],
    [2, 2, 2, 2, 2, 1, 0.666, 0.091, 0],
    [1, 3, 3, 1, 3, 2, 0.243, 0.267, 0],
    [3, 3, 3, 3, 3, 1, 0.245, 0.057, 0],
    [3, 1, 1, 3, 3, 2, 0.343, 0.099, 0],
    [1, 2, 1, 2, 1, 1, 0.639, 0.161, 0],
    [3, 2, 2, 2, 1, 1, 0.657, 0.198, 0],
    [2, 2, 1, 1, 2, 2, 0.360, 0.370, 0],
    [3, 1, 1, 3, 3, 1, 0.593, 0.042, 0],
    [1, 1, 2, 2, 2, 1, 0.719, 0.103, 0]])
m, n = D.shape[0], D.shape[1]-1  # 实例数,样本数
label = np.unique(D[:,-1])
class_dict = {int(l): 0 for l in label}
for i in range(m):
    class_dict[D[i,-1]] += 1
p_class = {l: (class_dict[l]+1)/(m+2) for l in class_dict}
DICT0 = [{} for item in range(n)]  # list of dicts that contain their own samples with class 0
DICT1 = [{} for item in range(n)]  # list of dicts that contain their own samples with class 1
 
for i, d in enumerate(DICT0[:-2]):
    DICT0[i] = {int(a): 0 for a in np.unique(D[:, i])}
    d = DICT0[i]
    k = len(np.unique(D[:, i]))  # 第i列中的属性数量
    for j in range(8):
        d[D[j,i]] += 1
    DICT0[i] = {l: (d[l]+1)/(8+k) for l in d}
 
for i, d in enumerate(DICT1[:-2]):
    DICT1[i] = {int(a): 0 for a in np.unique(D[:, i])}
    d = DICT1[i]
    k = len(np.unique(D[:, i]))  # 第i列中的属性数量
    for j in range(8,m):
        d[D[j, i]] += 1
    DICT1[i] = {l: (d[l] + 1) / (9 + k) for l in d}
 
def prob_continuous(x,data_n):  # 连续变量的概率
    mean = np.mean(data_n)
    var = np.var(data_n)
    p = np.exp(-(x-mean)**2*0.5/var)/(np.sqrt(2*np.pi*var))
    return p
 
test = [1,1,1,1,1,1,0.697,0.46]  # 预测样本
result = [p_class[0], p_class[1]]
DICT0[6], DICT0[7] = prob_continuous(test[-2], D[:8, 6]), prob_continuous(test[-1], D[:8, 7])
DICT1[6], DICT1[7] = prob_continuous(test[-2], D[8:, 6]), prob_continuous(test[-1], D[8:, 7])
 
for i, t in enumerate(test[:-2]):
    result[0] *= DICT0[i][t]
    result[1] *= DICT1[i][t]
result[0] *= DICT0[6] * DICT0[7]
result[1] *= DICT1[6] * DICT1[7]
print(result)

结果：

// An highlighted block
[0.024223607117715082, 4.4242506192749345e-05]

**结果分析：**由于0.024223607117715082>4.4242506192749345e-05，因此朴素贝叶斯分类器将测试样本判别为“好瓜”。
参考链接：
https://blog.csdn.net/qilixuening/article/details/68495402

第二种：

建立数据集：获取书中的西瓜数据集3.0，并存为data_3.txt

算法实现：

// An highlighted block
import math
import numpy as np
import pandas as pd
 
D_keys = {
	'色泽': ['青绿', '乌黑', '浅白'], 
	'根蒂': ['蜷缩', '硬挺', '稍蜷'], 
	'敲声': ['清脆', '沉闷', '浊响'], 
	'纹理': ['稍糊', '模糊', '清晰'], 
	'脐部': ['凹陷', '稍凹', '平坦'], 
	'触感': ['软粘', '硬滑'], 
}
Class, labels = '好瓜', ['是', '否']
 
# 读取数据
def loadData(filename):
	dataSet = pd.read_csv(filename)
	dataSet.drop(columns=['编号'], inplace=True)
	return dataSet
 
# 配置测1数据
def load_data_test():
	array = ['青绿', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', 0.697, 0.460, '']
	dic = {a: b for a, b in zip(dataSet.columns, array)}
	return dic
 
def calculate_D(dataSet):
	D = []
	for label in labels:
		temp = dataSet.loc[dataSet[Class]==label]
		D.append(temp)
 
	return D
 
def calculate_Pc(Dc, D):
	D_size = D.shape[0]
	Dc_size = Dc.shape[0]
	N = len(labels)
	return (Dc_size+1) / (D_size+N)
 
def calculate_Pcx_D(key, value, Dc):
	Dc_size = Dc.shape[0]
	Dcx_size = Dc[key].value_counts()[value]
	Ni = len(D_keys[key])
	return (Dcx_size+1) / (Dc_size+Ni)
 
def calculate_Pcx_C(key, value, Dc):
	mean, var = Dc[key].mean(), Dc[key].var()
	exponent = math.exp(-(math.pow(value-mean, 2) / (2*var)))
	return (1 / (math.sqrt(2*math.pi*var)) * exponent)
 
def calculate_probability(label, Dc, dataSet, data_test):
	prob = calculate_Pc(Dc, dataSet)
	for key in Dc.columns[:-1]:
		value = data_test[key]
		if key in D_keys:
			prob *= calculate_Pcx_D(key, value, Dc)
		else:
			prob *= calculate_Pcx_C(key, value, Dc)
 
	return prob
 
def predict(dataSet, data_test):
	# mu, sigma = dataSet.mean(), dataSet.var()
	Dcs = calculate_D(dataSet)
	max_prob = -1
	for label, Dc in zip(labels, Dcs):
		prob = calculate_probability(label, Dc, dataSet, data_test)
 
		if prob > max_prob:
			best_label = label
			max_prob = prob
 
		print(label, prob)
 
	return best_label
 
 
if __name__ == '__main__':
	# 读取数据
	filename = 'data_3.txt'
	dataSet = loadData(filename)
	data_test = load_data_test()
	label = predict(dataSet, data_test)
	print('预测结果：', label)

结果：

// An highlighted block
是 0.025631024529740663
否 7.722360621178048e-05
预测结果： 是

参考链接：
https://blog.csdn.net/qilixuening/article/details/68495402