MCMC采样

MCMC采样

MCMC 是一种随机的近似推断，其核心就是基于采样的随机近似方法蒙特卡洛方法。而近似推断中又可以分成两大类，即为确定性近似 (VI) 和随机近似 (MCMC)。我们需要从概率分布中取
个点，从而近似计算这个积分。常用采样方法有：逆采样，拒绝采样和重要性采样。

逆采样（Inverse Sampling）

首先求得概率密度的累积密度函数CDF，然后求得CDF的反函数，在0到1之间均匀采样$u^{(i)}\sim U(0,1)$，代入反函数，就得到了采样点$x^{(i)}\sim cd{f}^{-1}\left(u^{(i)}\right)$。但是实际大部分概率分布不能得到CDF。

下面我们以指数分布为例，说明如何通过均匀分布来采样服从指数分布的样本集。指数分布的概率密度函教PDF为：
$p_{\exp }(x)=\{\begin{array}{cc}\lambda \exp (-\lambda x)& ,x\ge 0\\ 0& ,x<0\end{array}$ (1)

那么它的概率分布函数CDF为：
$\mathrm{F}(\mathrm{x})={\int }_{-\infty }^{x}p(x)dx$ (2)

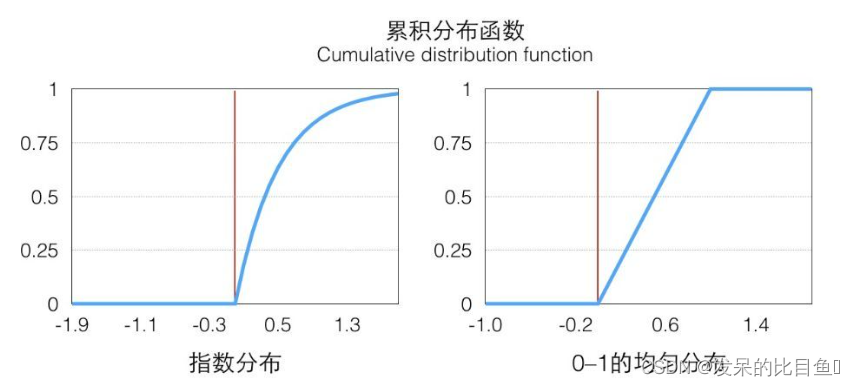
下图为指数分布和均匀分布的CDF图。从左图上看，在$x\ge 0$的部分是一个单调递增的函数(在定义域上单调非减)，定义域和值域是$[0,+\infty )\to [0,1)$，在$p(x)$大的地方它增长快，反之亦然。

因为它是唯一映射的（在$x>0$的部分，接下来我们只考虑这一部分），所以它的反函数可以表示为$F^{-1}(a),a\in [0,1)$，值域为$[0,+oo)$。（上图的左图就是$F(x)$的图）

因为$F$单调递增，所以$F^{-1}$也是单调递增的：
$\begin{array}{rl}& x\le y\Rightarrow F(x)\le F(y)\\ & a\le b\Rightarrow F^{-1}(a)\le F^{-1}(b)\end{array}$ (3)

利用反函数的定义，我们有：
$F^{-1}(a)<x\text{, if }a<F(x)$ (4)

接下来，我们定义一下$[0,1]$均匀分布的CDF，这个很好理解：
$P(a\le x)=H(x)=\{\begin{array}{cc}1& ,x\ge 1\\ x& ,0\le x\le 1\\ 0& ,x<0\end{array}$ (5)

根据公式(4) (5)得：
$P\left(F^{-1}(a)\le x\right)=P(a\le F(x))=H(F(x))$ (6)

因为$F(x)$的值域$[0，1)$，根据公式（5），公式（6）可以改写为：
$\mathrm{P}\left({\mathrm{F}}^{-1}(\mathrm{a})\le \mathrm{x}\right)=\mathrm{H}(\mathrm{F}(\mathrm{x}))=\mathrm{F}(\mathrm{x})$ (7)

据$F(x)$的定义，它是exp分布的CDF，所以公式（7）的意思是$F^{-1}(a)$ 符合exp分布，我们通过$F$的反函数将一个0到1均匀分布的随机数转换成了符合$exp$分布的随机数，注意，以上推导对于CDF可逆的分布都是一样的。对于exp来说，它的反函数的形式是：
$F_{\exp }^{-1}(a)=-\frac{1}{\lambda }\ast \log (1-a)$

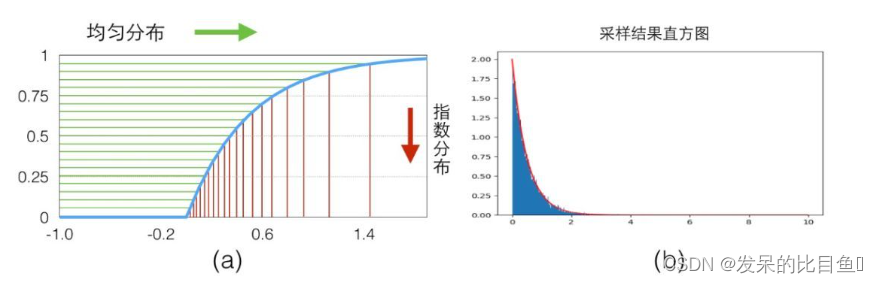
具体的映射关系可以看下图(a)， 我们从y轴0-1的均匀分布样本(绿色)映射得到了服从指数分布的样本(红色)。

代码

import numpy as np
import matplotlib.pyplot as plt
def sampleExp(Lambda = 2,maxCnt = 50000):
    ys = []
    standardXaxis = []
    standardExp = []
    for i in range(maxCnt):
        u = np.random.random()
        y = -1/Lambda*np.log(1-u) #F-1(X)
        ys.append(y)
    for i in range(1000):
        t = Lambda * np.exp(-Lambda*i/100)
        standardXaxis.append(i/100)
        standardExp.append(t)
    
    print()
    plt.plot(standardXaxis,standardExp,'r')
    plt.hist(ys,1000, density=True)
    plt.show()

sampleExp()

拒绝采样（Reject Sampling）

对于概率分布$p(Z)$，引入简单的提议分布$q(z)$，使得$\forall z_i,Mq\left(z_i\right)\ge p\left(z_i\right)$。首先在$q(z)$中采样，定义接受率：$\alpha =\frac{p\left(z^i\right)}{Mq\left(z^i\right)}\le 1$。

采样步骤:

1. 取 $z^i\sim q(z)$ 。
2. 在均匀分布中选取 $u$ 。
3. 如果 $u\le \alpha$ ，则接受 $z^i$ ，否则，拒绝这个值。

我们以求圆周率$\pi$的例子入手，讲解拒绝采样的思想。通过采样的方法来计算t值，也就是在一个1×1的范围内随机采样一个点，如果它到原点的距离小于1，则说明它在1/4圆内，则接受它，最后通过接受的占比来计算1/4圆形的面积，从而根据公式反算出预估$\pi$个的值，随着采样点的增多，最后的结果$\pi$人会越精准。

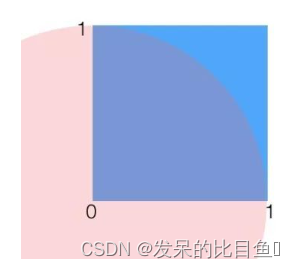
求一个空间里均匀分布的集合面积，可以尝试在更大范围内按照均匀分布随机采样，如果采样点在集合中，则接受，否则拒绝。最后的接受概率就是集合在”更大范围“的面积占比。

代码

def samplePI(maxCnt=10000000):
    accCnt = 0
    for _ in range(maxCnt):
        x = np.random.random()
        y = np.random.random()
        if np.sqrt(x**2+y**2)<1:
            accCnt += 1
    return (accCnt/maxCnt)*4

samplePI() 

推导.

给定一个概率分布$p(z)=\frac{1}{Z_p}\tilde{p}(z)$。 其中，$\tilde{\mathrm{p}}(z)$已知。$Z_p$为归一化常数， 未知， 要对该分布$p(z)$进行拒绝采样，首先需要借用一个简单的参考分布（proposal distribution），记为$q(x)$，该分布的采样易于实现，如均匀分布、高斯分布。
然后引入常数$k$，使得对所有的的$z$，满足$k\mathrm{q}(z)\ge \tilde{\mathrm{p}}(z)$，如下图所示，红色的曲线为$\tilde{\mathrm{p}}(\mathrm{z})$，蓝色的曲线为$\mathrm{kq}(\mathrm{z})$。

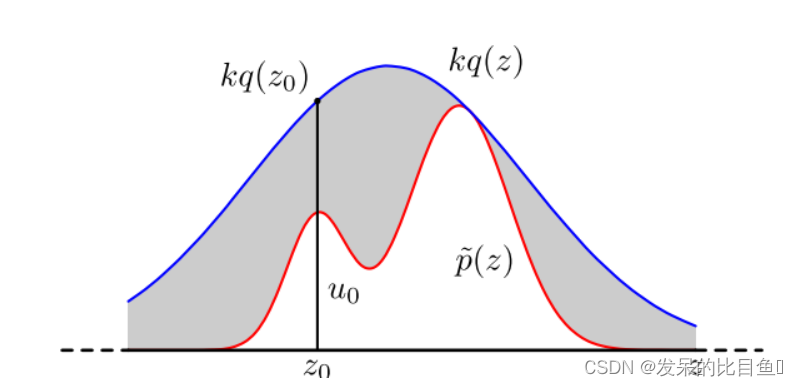
在每次采样中，首先从$q(z)$采样一个数值$z_0$，然后在区间$[0,kq(z_0)]$进行均匀采样，得到$u_0$。如果$u_0<p(z_0)$，则保留该采样值，否则舍弃该采样值。最后得到的数据就是对$p(z)$分布的一个近似采样。结合图，直观来理解上述的过程：在$x=z_0$这条线上，从$[0,kq(z_0)]$均匀采样中一个值，如果这个值小于$\tilde{\mathbf{p}}\left(z_0\right)$，即这个均匀采样的这个值落在了$\tilde{\mathbf{p}}\left(z_0\right)$的下方，我们就接受$z_0$这个采样值。

我们知道，每次采样的接受概率计算如下：
$$\mathrm{p}(\text{ accept })=\int \frac{\tilde{p}(z)}{\mathrm{kq}(z)}\mathrm{q}(z)\mathrm{d}z=\frac{1}{\mathrm{k}}\int \tilde{\mathrm{p}}(z)\mathrm{d}z$$

所以，为了提高接受概率，防止舍弃过多的采样值而导致采样效率低下，$k$的选取应该在满足$\mathrm{kq}(z)\ge \tilde{\mathrm{p}}(z)$的基础上尽可能小。

拒绝采样问题可以这样理解，$\tilde{p}(z)$与$x$轴之间的区域为要估计的问题，类似于上面提到的圆形区域，$kq(z)$与$x$轴之间的区域为参考区域，类似于上面提到的正方形。由于$kq(z)$与$x$轴之间的区域面积为$k$（原来的概率密度函数的面积为1，现在扩大了$k$倍，故$k\times 1$，所以，$p(z)$与$x$轴之间的区域面积除以$k$即为对$p(z)$的估计。在每一个采样点，以$[0，kq(z_0)]$为界限，落在$\tilde{\mathrm{p}}(\mathrm{z})$曲线以下的点就是服从$p(z)$分布的点。

假设，我们要采样的分布是：
$\tilde{p}(z)=0.3\exp \left(-(z-0.3{)}^2\right)+0.7\exp \left(-(z-2{)}^2/0.3\right)$。其归一化常数$Z_p\approx 1.2113$，参考分布为高斯分布$q(z)=\mathrm{Gassian}(1.4,1.2)$, 其中均值和方差是经过计算和尝试得到的，以满足$kq(z)\ge \tilde{\mathrm{p}}(z)$

代码

import numpy as np
import matplotlib.pyplot as plt

def f1(x):
    return (0.3*np.exp(-(x-0.3)**2) + 0.7* np.exp(-(x-2.)**2/0.3))/1.2113
x = np.arange(-4.,6.,0.01)
plt.plot(x,f1(x),color = "red")

size = int(1e+07)
sigma = 1.2
z = np.random.normal(loc = 1.4,scale = sigma, size = size)
qz = 1/(np.sqrt(2*np.pi)*sigma)*np.exp(-0.5*(z-1.4)**2/sigma**2)
k = 2.5
#z = np.random.uniform(low = -4, high = 6, size = size)
#qz = 0.1
#k = 10
u = np.random.uniform(low = 0, high = k*qz, size = size)

pz =  0.3*np.exp(-(z-0.3)**2) + 0.7* np.exp(-(z-2.)**2/0.3)
sample = z[pz >= u]
plt.hist(sample,bins=150, density=True, edgecolor='black')
plt.show()

重要性采样 （Importance Sampling）

重要性采样并不是直接对概率进行采样，而是对概率分布的期望进行采样${\mathbb{E}}_{p(z)}[f(z)]$。
$$\begin{array}{rl}{\mathbb{E}}_{p(z)}[f(z)]=\int p(z)f(z)dz& =\int \frac{p(z)}{q(z)}q(z)f(z)dz\\ & =\int f(z)\frac{p(z)}{q(z)}q(z)dz\\ & \approx \frac{1}{N}\sum _{i=1}^{N}f\left(z_i\right)\frac{p\left(z_i\right)}{q\left(z_i\right)}\\ & z_i\sim q(z),i=1,2,\cdots ,N\end{array}$$

其中$\frac{p\left(z_i\right)}{q\left(z_i\right)}$是重要性值（Weight），用来平衡不同的概率密度值之间的差距。重要值采样对于权重非常小的时候，效率非常低。重要性采样有一个变种 Sampling-Importance-Resampling，这种方法，首先和上面一样进行采样，然后在采样出来的$N$个样本中，重新采样，这个重新采样，使用每个样本点的权重作为概率分布进行采样。

下面就放一些比较重要的部分. 首先我们来定义函数f(x). 定义的函数如下:
$\frac{1}{1+\exp (-x)}$

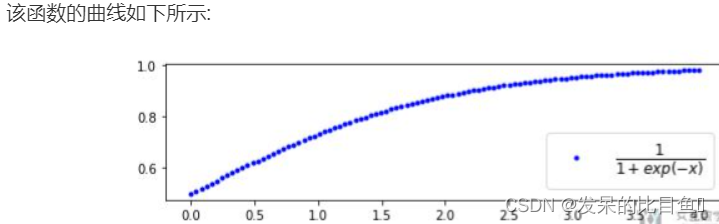
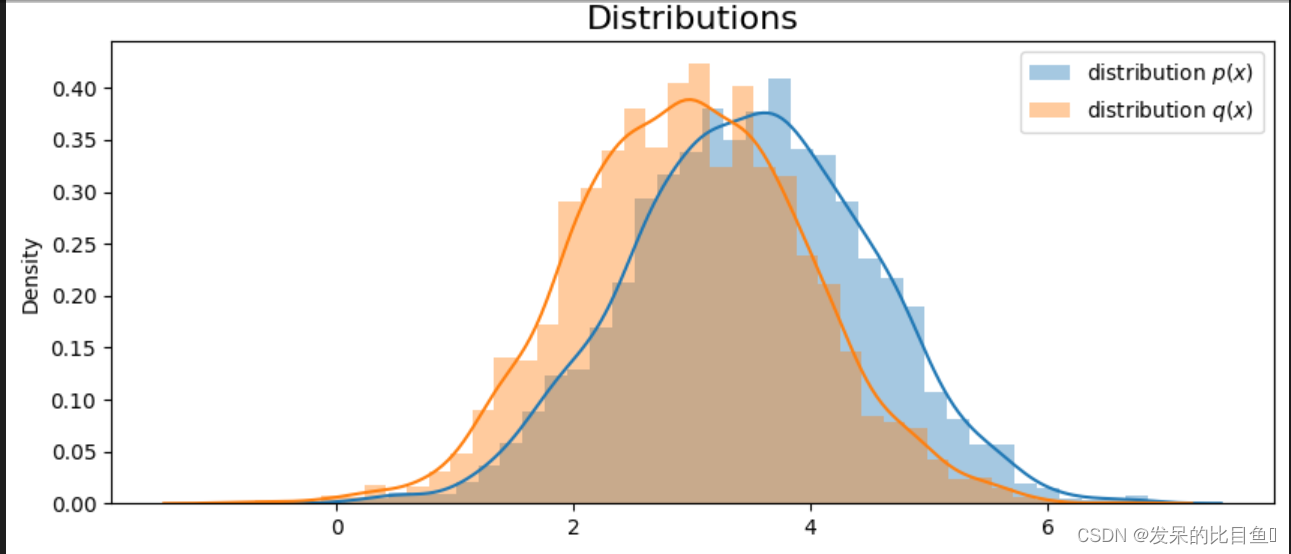
首先进行第一个实验, p(x)与q(x)比较接近. 下面我们来定义分布p(x)和q(x). 这两个分布的均值比较接近. 我们从每一个分布中抽样3000个数据.

# p(x)
mu_target = 3.5
sigma_target = 1
p_x = [np.random.normal(mu_target, sigma_target) for _ in range(3000)]
# q(x)
mu_appro = 3
sigma_appro = 1
q_x = [np.random.normal(mu_appro, sigma_appro) for _ in range(3000)]

fig = plt.figure(figsize=(10,6))
ax = fig.add_subplot(1,1,1)
# 画出两个分布的图像
sns.distplot(p_x, label="distribution $p(x)$")
sns.distplot(q_x, label="distribution $q(x)$")
plt.title("Distributions", size=16)
plt.legend()

最终这两个分布如下所示:

# 当x~p(x)时, E[f(x)]
np.mean([f_x(i) for i in p_x])

参考

https://www.cnblogs.com/yechangxin/articles/17017600.html