Cross-lingual Entity Alignment via Joint Attribute-Preserving Embedding(基于联合属性保持向量的跨语言实体对齐)

最新推荐文章于 2024-06-20 09:38:33 发布

球球不秃头

最新推荐文章于 2024-06-20 09:38:33 发布

阅读量1.4k

点赞数 2

分类专栏： NLP 文章标签：知识库嵌入跨语言实体对齐属性向量结构向量向量模型

NLP 专栏收录该内容

9 篇文章

订阅专栏

基于联合属性保持向量的跨语言实体对齐

1 引言
2 相关工作
- 2.1KB Embedding
- 2.2 跨语言知识库对齐
3 基于知识库嵌入的跨语言实体对齐

摘要实体对齐的任务是在两个知识库(KBs)中找到代表相同现实世界对象的实体。在面对不同自然语言的KBs时，传统的跨语言实体对齐方法依靠机器翻译来消除语言障碍。这些方法经常受到不同语言之间翻译质量不均衡的影响。虽然最近的基于embedding的技术在KBs中编码实体和关系，并且不需要机器翻译来实现跨语言实体对齐，但仍有大量属性未被探索。本文提出了一种 用于跨语言实体对齐的联合属性保持向量模型。它将两个KBs的结构 共同嵌入到一个统一的向量空间中，并 利用KBs中的属性相关性进一步细化。我们在真实数据集上的实验结果表明，该方法显著优于目前最先进的跨语言实体对齐嵌入方法，并可以与基于机器翻译的方法相补充。

1 引言

在过去的几年中，知识库（KBs）已经成功地应用于许多人工智能相关领域，如语义Web、问答和Web挖掘。各种知识库覆盖广泛的领域，存储丰富、结构化的真实世界事实。在KB中，每个事实都以三元组的形式（实体、属性、值）表示，其中值可以是文字或实体。实体、属性、文字和三元组分别用E、P、L和T表示。为简单起见，将忽略空白节点。有两种类型的属性——关系(R)和属性(A)——相应地也有两种三元组，即关系三元组和属性三元组。关系三元组 $t r \in E \times R \times E$ 描述了两个实体之间的关系，而属性三元组 $t r \in E \times A \times L$ 给出实体的文字属性值。

众所周知，知识库系统经常面临两个问题：

覆盖率低。不同方使用不同的数据源构建不同的知识库。它们包含互补的事实，因此必须集成多个知识库；
多语种差异。为了支持多语言应用程序，已经构建了越来越多的多语言知识库和特定语言知识库。这使得整合跨语言知识库既有必要也有好处。

实体对齐的任务是在两个KB中查找引用同一真实世界对象的实体。它在自动集成多个知识库方面起着至关重要的作用。本文主要研究跨语言实体对齐。它可以帮助构建一个连贯的知识库，并处理跨不同自然语言的不同知识表达。传统的跨语言实体对齐方法依赖于机器翻译，其精度还远远不够理想。Spohret等人认为，跨语言场景中的对齐质量在很大程度上取决于多种语言之间的翻译质量。

继流行的基于翻译的 embedding 模型之后，一些研究利用KB向量进行实体对齐，并取得了有希望的结果。embedding技术学习低维向量表示（即embedding），并将各种语义(如类型)编码到其中。以知识库结构为重点，基于 embedding 的方法提供了一种跨语言实体对齐的替代方法，而不考虑其自然语言标签。

将 embedding 方法应用于跨语言实体对齐仍然存在一些挑战。首先，据我们所知，大多数现有的知识库 embedding 模型仅基于关系三元组学习 embedding。然而，我们观察到属性三元组占了KBs的很大一部分。例如，我们从English DBpedia(2016-04)中统计infobox事实的三元组，发现了58,181,947个属性三元组，是关系三元组(数目为18,598,409)的三倍。面对实体对齐的任务，属性三元组可以提供额外的信息来向量化实体，但是如何将它们合并到跨语言嵌入模型中仍然没有得到很大的研究。其次，由于链接开放数据倡议，知识库之间存在一些对齐的实体和属性，可以作为它们之间的桥梁。然而，正如[5]中所发现的，跨语言知识库之间的现有对齐通常只占一小部分。因此，如何更好地利用它是向量化跨语言知识库的关键。

为了解决上述问题，我们引入了一种联合保持属性的向量模型，用于跨语言实体对齐。它采用结构向量(SE)和属性向量(AE)两个模块，分别在两个知识库中基于两个知识层面(关系三元组和属性三元组)学习向量。SE专注于建模两个KBs的关系结构，并利用预先给定的现有对齐作为重叠其结构的桥梁。AE捕获属性的相关性(即这些属性是否通常一起用于描述一个实体)，并基于属性相关性对实体进行聚类。最后，结合SE和AE，将两个KBs中的所有实体共同嵌入到一个统一的向量空间 $\mathbb R^d$ 中，其中为向量的维数。我们的方法的目的是通过搜索源实体在 $\mathbb R^d$ 中最临近来找到潜在的跨语言目标实体(即我们想要发现的真正对齐的实体)。我们希望潜在对齐的跨语言实体的向量彼此非常接近。

综上所述，本文的主要贡献如下:

我们提出了一种基于向量的跨语言实体对齐方法，该方法不依赖于跨语言KBs之间的机器翻译。
利用结构向量的方法联合向量化两个KBs的关系三元组，利用属性向量的KBs属性三元组进一步细化向量化。据我们所知，保留它们的属性信息时，跨语言KBs没有预先学习向量。
我们对来自DBpedia的真实世界跨语言数据集进行了评估。实验结果表明，我们的方法在很大程度上优于两种先进的基于向量的跨语言实体对齐方法。此外，它可以与传统的基于机器翻译的方法相补充。

本文的其余部分组织如下。我们在第2节讨论了知识库向量和跨语言知识库对齐的相关工作。我们在第3节详细描述了我们的方法，并在第4节报告了实验结果。最后，我们在第5节总结了本文和未来的工作。

2 相关工作

我们将相关工作分为两个子领域：知识库 Embedding 和跨语言知识库对齐。我们将在本节的其余部分讨论它们。

2.1KB Embedding

近年来，人们在学习 KB Embedding 方面做出了巨大的努力。TransE是基于翻译的方法的先驱，将关系向量解释为从头部实体向量到尾部实体向量的转换。换句话说，如果一个关系三元组（h，r，t）成立， $h + r \approx t$ 这是意料之中的事。TransE显示了其建模1对1关系的强大能力，并在知识库完成方面取得了有希望的结果。为了进一步改进TransE，提出了包括TransH和TransR在内的后续工作。此外，还有一些基于非翻译的 KB Embedding 方法。

此外，也有一些研究利用KBs的知识来改进嵌入。krompa ß等人在KB Embedding 模型中增加了类型约束，提高了其链路预测性能。KR-EAR通过对属性相关性建模，额外嵌入属性，在实体、关系和属性预测方面取得了良好的效果。但它只学习单个知识库中的属性嵌入，这阻碍了它在跨语言情况下的应用。此外，KR-EAR关注的是那些值来自一小组条目的属性，例如“gender”的值是{Female, Male}。它可能无法建模那些值非常稀疏和异构的属性，例如“name”、“label”和“coordinate”。RDF2Vec使用KB结构的局部信息来生成实体序列，并使用语言建模方法来学习用于机器学习任务的实体嵌入。对于跨语言任务，[12]扩展了NTNKBC用于跨语言KB完成。[7]采用神经网络方法，将英文KBs翻译成中文，扩大中文KBs。

2.2 跨语言知识库对齐

现有的跨语言知识库对齐工作主要分为两类：跨语言本体匹配和跨语言实体对齐。对于跨语言本体匹配，Fuet等提出了一个通用框架，利用机器翻译工具将标签翻译为同一语言，使用单语言本体匹配方法查找映射。Spohret等利用基于翻译的标签相似性和本体结构作为机器学习技术(如支持向量机)学习跨语言映射功能的特征。在所有这些工作中，机器翻译是一个不可分割的组成部分。

对于跨语言实体对齐，MTransE结合TransE将KB结构编码到语言特定的向量空间，并设计了5个对齐模型，通过种子对齐来学习不同语言KBs之间的翻译。JE利用TransE将不同的KBs嵌入到一个统一的空间，目的是每个种子对齐都有类似的 embedding ，这是可扩展到跨语言场景。Wanget al.提出了一个图模型，它只利用语言独立的特性(例如out-/ links)来查找Wiki知识库之间的跨语言链接。利用了基于 Embedding 的方法来对齐Web表中的实体。与之不同的是，我们的方法将两个KBs联合嵌入在一起，利用属性 embedding 进行改进。

3 基于知识库嵌入的跨语言实体对齐

在本节中，我们首先介绍了我们的联合属性保持嵌入模型的表示法和一般框架。然后，我们详细阐述了模型的技术细节，并讨论了几个关键的设计问题。

我们使用小写粗体字母来表示相应术语的向量表示，例如， $(\mathbf h, \mathbf r, \mathbf t)$ 为三元组 $(h, r, t)$ 的向量表示。我们用大写粗体字母表示矩阵，用上标表示不同的 KBs。例如， $E^{(1)}$ 表示KB1中实体的表示矩阵，其中每一行都是实体向量 $e^{(1)}$ 。

3.1 概述

我们的联合属性保持嵌入模型的框架如图1所示。给定两个不同自然语言的KBs(表示为KB1和KB2)和一些预对齐的实体或属性对(称为种子对齐，用上标 $^{(1,2)}$ 表示)，我们的模型学习KB1和KB2的向量表示，并期望潜在的对齐实体紧密嵌入。
在这里插入图片描述
图1：联合属性保持嵌入模型的框架

在TransE之后，我们将关系解释为从头实体到尾实体的转换，来表征KBs的结构信息。我们让种子对齐中的每一对共享相同的表示，作为KB1和KB2之间的桥梁，构建叠加关系图，并通过结构向量(structure embedding, SE)联合学习统一向量空间下所有实体的表示。直觉是，两个可对齐的KBs可能有许多对齐的三元组，例如英语的(Washington, capitalOf, America)和法语的对应(Washington, capitaleDes, Etats-Unis)。在此基础上，SE旨在学习两个KBs之间的潜在对齐三元的近似表示。

然而，SE只要求学习的表示必须在每个关系三元组内兼容，这导致一些实体由于它们的关系三元组的稀疏性而无序分布。为了缓解这种非相干分布，我们利用属性三元组来帮助嵌入实体，因为我们观察到潜在的对齐实体通常在属性值上具有高度的相似性。从技术上讲，由于属性值的复杂性、异质性和跨语言性，我们忽略了它们。相反，我们将属性值抽象为它们的范围类型，例如(Tom, age， " 12 “)到(Tom, age, Integer)，其中Integer是值” 12 "的抽象范围类型。然后，对抽象属性三元组进行属性向量(AE)，获取跨语言和单语言属性的相关性，并在此基础上计算实体的相似性。最后，将属性相似度约束与SE相结合，通过聚类具有高属性相关性的实体来细化表示。这样，我们的联合模型既保留了两个KBs的关系信息，又保留了它们的属性信息。

将实体以向量形式表示在统一的嵌入空间中，通过搜索该空间中最近的跨语言邻居，可以实现潜在跨语言目标实体对源实体的对齐。

3.2 结构向量

SE的目的是模拟两个KBs的几何结构，并学习潜在的对齐三元的近似表示。形式上，给定一个关系三元组 $t r = (h, r, t)$ ，我们期望 $h + r = t$ 。为了测量 $t r$ 的可信度，我们定义了评分函数 $={||\mathbf h+\mathbf r−\mathbf t||}^2_2$ 。我们希望 $f (t r)$ 的值更低，并希望对每个关系三元组将其最小化。

图2给出了一个例子，说明SE如何用种子对齐来建模两个KBs的几何结构。

在阶段(1)中，我们随机初始化所有的向量，并让种子对齐中的每对向量重叠，构建覆盖关系图。为了在图中直观地表示出三元组，我们将实体视为向量空间中的一个点，将关系向量从其头部实体开始移动。注意，目前实体和关系是随机分布的。
在阶段(2)中，我们最小化三元组的分数，并让每个三元关系中的向量表示兼容。例如，关系capitalOf往往接近capitaleDes，因为它们共享相同的头实体和尾实体。与此同时，实体“America”和它的近似“ ´Etats-Unis”将紧密地移动到彼此之间，因为它们有共同的头部实体和近似的关系。因此，SE是一个动态的传播过程。训练后的理想状态显示为Phase(3)。我们可以看到潜在的结盟实体“America”和“ ´Etats-Unis”在一起。

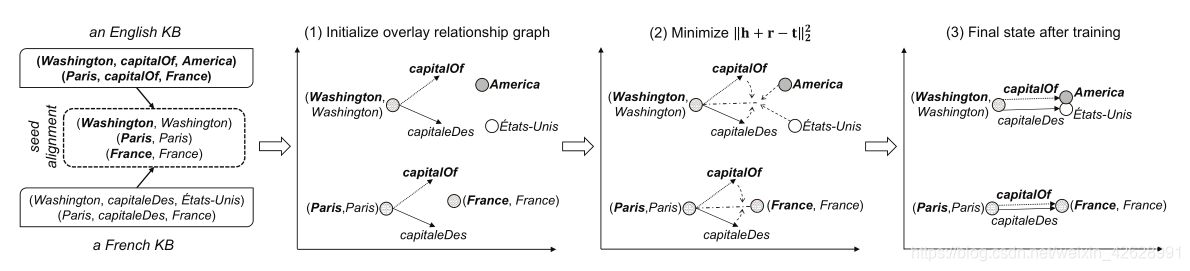
在这里插入图片描述
图2：结构向量实例

此外，我们发现在基于翻译的 embedding 模型中广泛使用的负三元组(也称为**损坏三元组)**对SE也有价值。考虑到另一个英国实体中国和它潜在的法国实体中国恰好与美国紧密相连，SE可能会把中国当成美国的候选人，因为他们距离很近。负三元组将有助于减少这种巧合的发生。如果我们把 $t r^{'} = (W a s h i n g t o n, c a p i t a l O f, C h i n a)$ 设为负三元组，并且把 $t r^{'}$ 设为高分，那么中国就会与美国保持距离。当我们强制任何嵌入向量的长度为1时，score函数有一个常数最大值。因此，我们希望最小化 $- f (t r^{'})$ 以获得 $t r^{'}$ 的高分。

综上所述，我们倾向于对已有的三元组(正的)评分较低，对负的评分较高，这样可以使以下目标函数最小化:
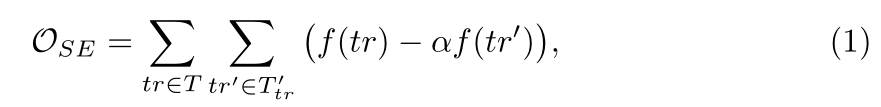
在这里插入图片描述
其中， $T$ 为所有正三元组的集合， $T'_{tr}$ 为 $t r$ 的相关负三元组，由一个随机实体(但不是同时)替换它的头或尾生成。 $α$ 是一个权重为正负三元组的比值超参数，其范围为 $[0, 1]$ 。重要的是要记住，种子对齐中的每一对在训练期间共享相同的向量，以便连接两个KBs。

3.3 属性向量与实体相似度计算

属性向量

如果一组属性通常被一起使用来描述一个实体，我们称它们为相关的。例如，经度、纬度和地名的属性是相互关联的，因为它们被广泛地一起用来描述一个地方。此外，我们希望赋予经度和纬度对较高的相关性，因为它们具有相同的范围类型。我们使用种子实体对来建立跨语言属性之间的相关性。给定一个对齐的实体对 $e^{(1)}, e^{(2)})$ ，我们将 $e^{(1)}$ 的属性视为 $e^{(2)}$ 的每个属性的相关属性，反之亦然。我们期望具有高度相关性的属性被紧密地嵌入。

为了捕捉属性的相关性，AE借鉴了Skip-gram的想法，这是一个非常流行的模型，通过预测一个单词本身的上下文来学习单词向量。类似地，给定一个属性，AE希望预测其相关属性。为了利用范围类型信息，AE最小化以下目标函数:
在这里插入图片描述
其中 $H$ 表示正 $(a, c)$ 对的集合，即 $c$ 实际上是a的相关属性，术语 $p (c ∣ a)$ 表示概率。为防止所有向量的值相同，我们采用负采样方法，有效地将 Eq.(2) 参数化，将 $log\ p (c|a)$ 替换为:

其中， $=\dfrac{1}{1+e^{−x}}$ . $H'_a$ 是根据对数均匀基数分布生成的属性 $a$ 的负对集合，假设它们都是错误的。如果 $a$ 和 $c$ 有不同的range类型，我们设 $w_{a,c}= 1$ ，否则设 $w_{a,c}= 2$ ，以增加它们趋于相似的概率。在本文中，我们区分了四种抽象范围类型，即Integer、Double、Datetime和String(默认)。注意，扩展到更多类型是很容易的。

实体相似度计算

给定属性嵌入，我们取实体的表示为其属性向量的归一化平均，即 $\mathbf{e} ={\Huge } {[\sum _{a \in A_e}\mathbf{a} ]}_1$ ，其中$ A_e$ 为 $e$ 的属性集， ${[.]}_1$ 表示归一化向量。我们有两个向量表示两个 KB 中的实体的矩阵， $\mathbf {E} _{AE}^{(1)} \in \mathbb {R}^{n_{e}^{(1)} \times d}$ 表示 KB1, $\mathbf {E} _{AE}^{(2)} \in \mathbb {R}^{n_{e}^{(2)} \times d}$ 表示 KB2，其中每一行是一个实体向量， $n_{e}^{(1)}$ ， $n_{e}^{(2)}$ 分别表示KB1, KB2中的实体数量。

我们使用余弦距离来衡量实体之间的相似性。对于两个实体 $e,e^′$ ，我们有 $sim(e,e^′)=cos(e,e^′)=\dfrac{e·e^′}{||e|| ||e'||}= e·e^′$ ，因为任何嵌入向量的长度都强制为1。KB1和KB2之间的交叉KB相似矩阵 $\mathbf S^{(1,2)}∈\mathbb R^{n^{(1)}_e×n^{(2)}_e}$ ，以及KB1的内部相似矩阵 $\mathbf S^{(1)}∈R^{n^{(1)}_e×n^{(1)}_e}$ 和KB2的 $\mathbf S^{(2)}∈R^{n^{(2)}_e×n^{(2)}_e}$ ，定义如下:
在这里插入图片描述
相似性矩阵 $S$ 表示实体之间的余弦相似性，并且 $S_{i,j}$ 是一个KB中的第 $i$ 个实体与同一或另一个KB中的第 $j$ 个实体之间的相似性。我们丢弃较低的 $S$ 值，因为两个实体的低相似性表明它们可能是不同的。因此，当 $S_{i,j}< τ$ 时，我们设置元素 $S_{i,j}= 0$ ，其中 $τ$ 是一个阈值，可以根据种子实体对的平均相似度来设置。在本文中，我们将内部相似性矩阵和交叉KB相似性矩阵的 $τ$ 分别固定为 $0.95$ 和 $0.9$ ，以达到较高的精度。

3.4 联合保持属性的嵌入

我们希望对KBs中的类似实体进行集群，以改进它们的向量表示。受[25]启发，我们使用实体之间的成对相似性矩阵作为监督信息，最小化以下目标函数：
在这里插入图片描述
其中 $β$ 是一个超参数，平衡KBs之间的相似性和他们的内在相似性。 $\mathbf E_{SE}∈\mathbb R^{n_e×d}$ 表示 SE 中 KB 的实体向量矩阵，每一行都是一个实体向量。 $\mathbf S^{(1,2)}E^{(2)}_{SE}$ 通过对KB2中实体向量的相似性进行积累，计算出KB1中实体的潜在向量。通过最小化 ${||\mathbf E^{(1)}_{SE}−\mathbf S^{(1,2)}\mathbf E^{(2)}_{SE}||}^2_F$ ，我们期望KBs之间紧密嵌入类似的实体。两个内部相似矩阵以相同的方式工作。

为了保持两个KBs的结构和属性信息，我们共同最小化以下目标函数:
在这里插入图片描述
其中 $δ$ 是 $\mathcal O_S$ 的超参数权重。

3.5 讨论

我们从以下几个方面对我们的联合属性保持嵌入模型进行了讨论和分析:

结构嵌入的目标函数

SE是基于翻译的嵌入模型，但其目标函数(见式(1))不遵循下面许多KB嵌入模型所使用的基于边缘的排名损失函数:
在这里插入图片描述
Eq.(7)旨在区分正、负三元组，期望它们的分数能有较大的差距。然而，对于跨语言实体对齐任务，我们除了要让他们的分数之间有较大的差距外，我们还希望将较低的分数分配给积极的三元组，将较高的分数分配给消极的三元组。因此我们选择Eq.(1)而不是Eq.(7)。

相比之下，JE使用来自TransE的基于边缘的排名损失，而MTransE没有这个，因为它不使用负三元组。然而，正如第3.2节所解释的，我们认为负三元组在区分实体之间的关系方面是有效的。我们在第4.4节报告的实验结果也证明了负三元组的有效性。

训练

我们用截断的正态分布随机初始化实体、关系和属性的向量等参数，然后优化等式 $(2) (6)$ 使用称为 $A d a G r a d$ 的梯度下降优化算法。我们的培训过程不是直接优化 $\mathcal O_{joint}$ ，而是使用两个优化器分别最小化 $\mathcal O_{SE}$ 和 $δ\mathcal O_S$ 。在每个阶段，两个优化器交替执行。当最小化 $O_{SE}$ 时， $f (t r)$ 和 $- α f (t r')$ 也可以交替优化。

任何嵌入向量的长度都被强制为1，原因如下：

该约束通过增加嵌入范数和塑造嵌入来防止训练过程简单地最小化目标函数；
它限制了训练过程中实体和关系分布的随机性；
它修复了等式(3)中的内积和余弦相似性之间的不匹配，以测量嵌入。

我们的模型在培训中也具有可扩展性。结构嵌入属于基于翻译的嵌入模型，已经被证明能够大规模学习嵌入[1]。为了节省内存，我们对等式(5)中的矩阵使用稀疏表示。此外，可以使用分治策略降低计算等式(4)的内存成本。

参数复杂性

联合模型中的参数数为 $d(n_e+n_r+n_a)$ ，其中 $n_e$ 、 $n_r$ 、 $n_a$ 分别为实体数、关系数和属性数。d是向量的尺寸。考虑到 $n r$ ， $n a ≪ n e$ 在实践中和训练中的种子对齐共享向量，模型的复杂性大致与实体的数量成线性关系。

搜索潜在对齐实体

因为每个向量的长度总是等于1，所以两个KBs的实体之间的余弦距离可以计算为 $\mathbf D=\mathbf E^{(1)}_{SE}\mathbf E^{(2)⊤}_{SE}$ 。因此，只需按降序对 $D$ 中的每一行进行排序，就可以得到最近的实体。对于每个源实体，我们希望它真正对齐的目标实体的排名是前几个。