零极点的左半平面/右半平面什么意思

神仙来了我也爱吃火锅

已于 2025-01-18 17:53:14 修改

阅读量3.8k

点赞数 69

分类专栏：模拟IC设计文章标签：硬件架构

于 2024-11-10 16:53:06 首次发布

本文链接：https://blog.csdn.net/weixin_42636352/article/details/143417006

版权

模拟IC设计专栏收录该内容

12 篇文章

订阅专栏

在我们从事模拟电子电路的工作过程中，经常会遇到分析零极点的情况。也经常会查阅资料，看到说该零/极点是左半平面或右半平面零/极点，所以blabla……

那么什么是系统的左右半平面零极点呢？我们又如何去理解它，利用它，最终的能从0到1的去分析它？

理解零极点的左右半平面，先得理解

一、左右半平面是什么的左右半平面?——也即坐标系是什么？

首先说，这个坐标系画的是什么的零极点？一般情况下，该坐标系是用来绘制一个信号系统的系统函数的。如下图，为最基本的反馈系统图，

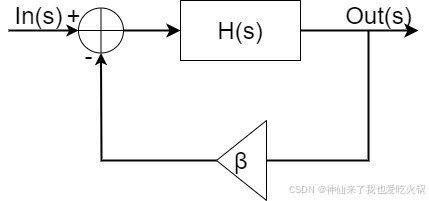
其对应的系统函数，为

$F\left ( s \right )=\frac{H\left ( s \right )}{1+\beta H\left ( s \right )}$

。可见该公式，一般为拉普拉斯变换的函数，如果用傅里叶变换，我们面对的函数可以写成

$F\left ( j\omega \right )=\frac{H\left ( j\omega \right )}{1+\beta H\left ( j\omega \right )}$

。实际一个意思。假设该函数是有两个极点，一个零点，那么函数一定可以变化成下式的形状，

$F\left ( s \right )=\frac{as+b}{cs^{2}+ds+e}$

进而变化成

$F\left ( s \right )=\frac{a\left ( s-z_{zeropoint} \right )}{c\left ( s-p_{polepoint1} \right )\left ( s-p_{polepoint2}\right )}$

通过解该函数，往往可以得到该函数对应的解，该解可能为实数，也可能为复数。我们就姑且全认为是复数了，得到三个解

$z_{zeropoint}=r_{zero}+j\omega _{zero}$

$p_{polepoint1}=r_{pole1}+j\omega _{pole1}$

$p_{polepoint2}=r_{pole2}+j\omega _{pole2}$

然后我们可以根据该函数计算出系统的零极点，绘制在坐标系中。可见，坐标系为一个复数坐标系，横轴为实数轴，竖轴为虚数轴。此处我将实数轴的字母使用了r表示，没有用传统的Re[]和Im【】，其中深意看后文就能明白。

二、零极点数值的意义是什么？——实部和虚部分别是什么？

前面的内容，已经明白坐标轴是什么。那么现在零极点的问题，就是实轴和虚轴具体是什么了。文章主题讨论的是电子电路，那么自然应该对应到电子电路上。

这个问题的真实本质，实际上是为什么电路系统分析的时候要引入复变函数的概念。在此，我特别想吐槽一下，““实数”“虚数”两个词，翻译得真的不怎么好。"虚"字容易给人一种“虚数”就是不存在的数的感觉。“复数”的本质，应该是二维数，虚数的本质，也只是二维数的另一维而已。复变函数，说白了就是就是二维向量的计算。

在信号领域，分析问题时，对于复杂的模型，几乎形成了一种固定方案，就是进行系统函数的傅里叶变换。因为再信号领域，每一个信号其实都带有两个参数，一个是当前信号点所在的时间点，另一个是当前信号点所拥有的信号幅值。用傅里叶变换，可以很好地将两个信号独立出去。傅里叶变换体现出了极强的周期性。因此可以用极坐标方式表现出来。如下面的gif图。

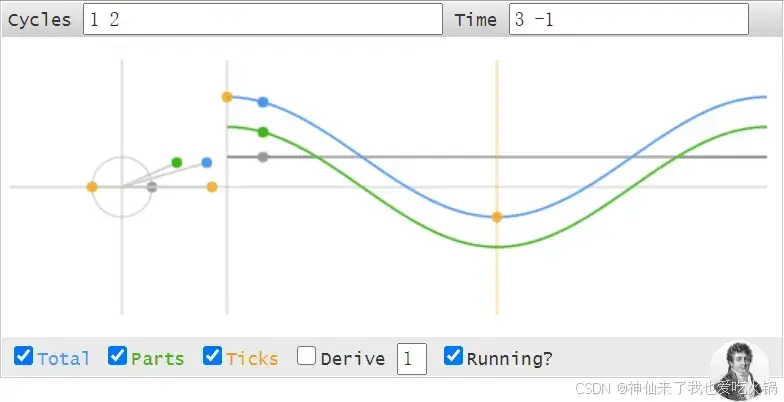
很明显，一个系统函数就一定是可以这样表示出来的了。只是系统函数可能不会像上图中三角函数这样的规整。

此时，对于图中的坐标系，左侧图中每一个点，距离原点的位置，就是右侧波形图的Y轴数值，也可以说其实就是振幅了。坐标中的每一个点与原点之间的连线，与实轴正半轴之间会有一个角度，这就是其实表达的是信号在每一个周期内当前的时间点。假设转动的速度，也即角频率是 $\omega$ ，则每一个点的角度就是 $\omega t$ 。从图中，我们也可以看出来，所谓的零点，其实就是振幅为0的点，所谓的极点，则是振幅为无穷大的点。

回到主题，不管是是零点还是极点，它都是系统函数的一个解。系统函数的解是什么——也即s是什么？直接说答案，s是在某一个频率下，系统中某个零极点节点看到的阻抗。那么它的实数部分，也即不含有相位的部分，自然是纯电阻；而它的虚数部分，含有相位，自然就是电感电容的影响了。此时，就可以理解为什么前文将虚数表示成 $r_{zero}+j\omega _{zero}$ 的形式。

假设极点处于左半平面，则r部分为负值；处于右半平面，则r部分为正值。这时候朋友们或许就愤怒了，“啥玩意儿，电阻怎么能是负的？”——能，见下图。

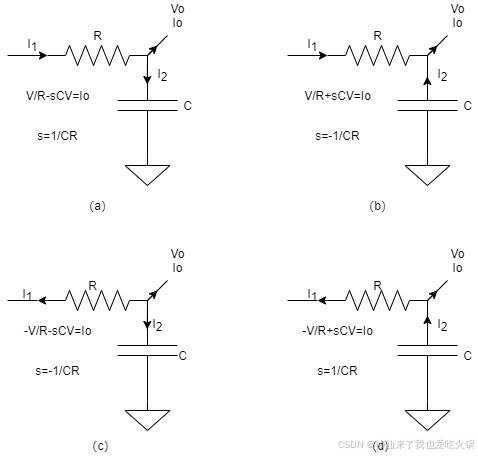
在图中，只要电阻和电容的电流方向不一致时，就会出现极点计算的s为复数的情况。

这怎么理解呢？

其实就是，电容此时的电流方向，与电阻不一致，那么电压越大的时候，其增加的电流必然一部分倒灌进入电阻中，那么岂不是电压越大，倒灌的越多，在电阻上看到的就是电压越大电流越小。那可不就成了负电阻了么。——说句非人话，就是此时电容的相位到了后半段，进入放电阶段了（a b 图情形）。

三、如何在电路中对应？——具体是个什么物理意义？

如前文所述，如果在左半平面，则电阻为负，其实也表现出此时电阻和电容电流方向不一致的情形。以极点为例，如下图。

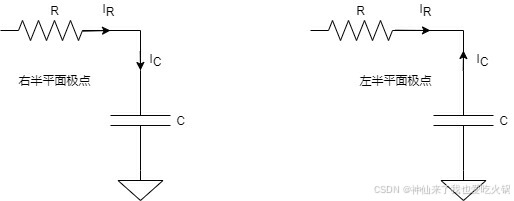
如果以零点为例呢？关键是我们如何去从电路中判断？来，来，来，我们再做一个假设，假设有这样一个电路，熟悉吧，不特殊吧。

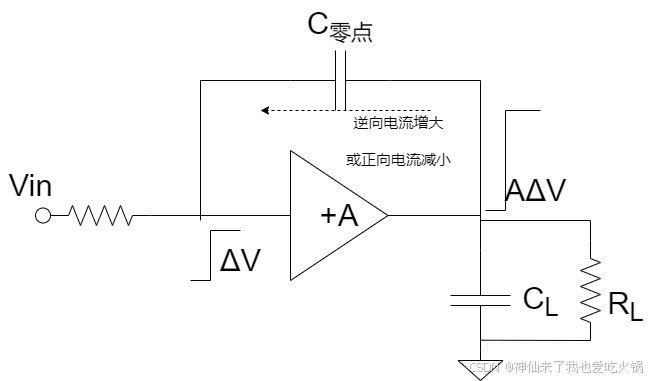
在这个图中，当放大器为正向放大的时候，输入每增大ΔV，输出增大更多，必然导致输入输出之间的压差为（A-1）ΔV。这样，加载在零点电容上的电压就更大，进而导致零点电容上的逆向电流增大，或者正向电流减小。电压越大，压差越大，逆向电流越大或者正向电流越小，这可不就是个负电阻么。（为什么这个电容是零点电容，请参考我另外一篇博文——什么是电路系统的零极点_零极点分析-CSDN博客）

那如果放大器为反向放大的时候，输入输出影响方式相反。自然就导致正电阻的现象了。如下图。

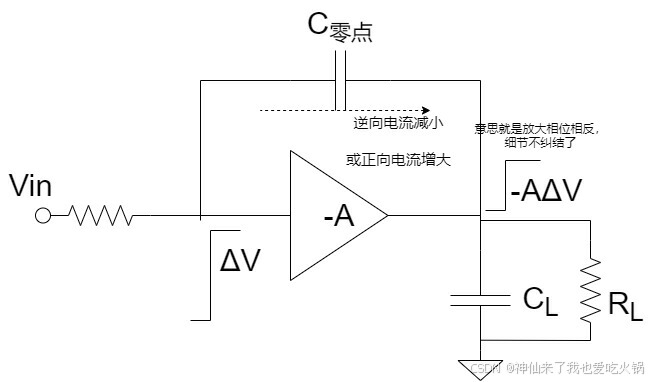
所以，在某些共源极电路中，会有个正半平面零点，在共漏极电路中，有负半平面零点。如下图，（相信大家能看懂，我就不细节标注哪个是共源那个是共漏，也不标注每个器件是干嘛的了）。

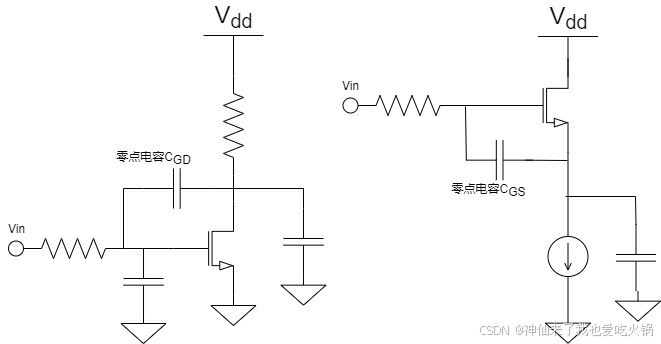
这些正负半平面零点的分布，也完全可能跟随着负载不同而变化。如共源极电路中，如果负载是个电阻，那么当然，放大倍数就是负数，零点自然是个正半平面零点。可是如果负载是个电感呢？我没自己推算，可以想象，我们一定有办法将放大倍数变成正数。那时候，零点就到了负半平面了。这些都要具体情况具体分析。本文的目的，在于理解正半平面，负半平面的物理意义，多的内容，暂时不展开了。

创作不易，可以说是太累了，朋友们一定要大胆点赞、收藏、关注，不要不好意思，不然，我坚持不下去了。谢谢

~完~