《机器人学》 二、关于在坐标系中旋转平移物体的理论基础解析

二、2D到3D的坐标变换问题

关于2d旋转变换问题在第一篇已经讲过，大概再整理基本内容，如下图：

3D旋转问题如下：
1、三维旋转可借助二维旋转来理解，由于三维空间中可以任意轴旋转，为方便分析与使用，只考虑绕X、Y、Z轴的旋转。
![在这里插入图片描述](https://img-blog.csdnimg.cn/direct/99b3e272cd5c444790f13f4c600aa67b.png

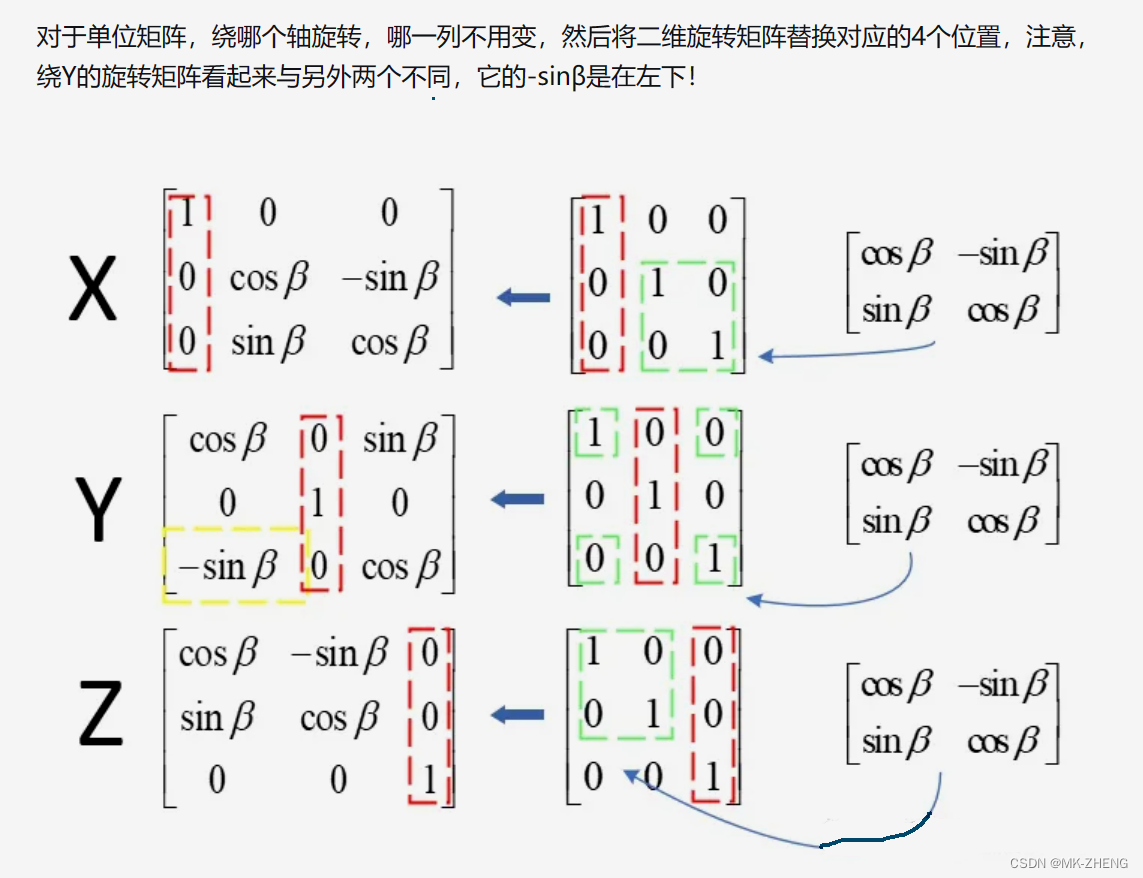
进阶：
以上我们得到了三个旋转矩阵，分别是绕x轴旋转，绕y轴旋转，绕z轴旋转，下面我们开始定义操作。

定义旋转操作

旋转单次
我们定义：
绕x轴旋转为操作A;
绕y轴旋转为操作B;
绕z轴旋转为操作C。

如果一个物体R想要绕x轴旋转t角度，得到一个新的物体位置R’，我们可以写为
R’ = A(t)R
其中R与R’就是坐标向量，A与R之间是向量乘法，A(t)代表的是绕x轴转角度t。
当然，一个物体不可能只有一个坐标点，如果存在多个坐标点R1,R2,R3，那么就一一乘上A(t)即可，也就是R1’=A(t)R1, R2’=A(t)R2, R3’=A(t)R3，最后得到新的物体的三个坐标点R1’, R2’, R3’。

连续多次旋转
如果我们想让这个物体首先绕x轴旋转角度t1，然后再绕y轴旋转角度t2，再绕z轴旋转角度t3，那么我们该怎么写？

我们一步一步看，首先是绕x轴旋转角度t1，公式为R’=A(t1)R。此时旋转后的物体的坐标是R’。

然后是绕y轴旋转角度t2，公式为R”=B(t2)R’。此时旋转后的物体的坐标是R”。

最后是绕z轴旋转角度r3，公式为R”’=C(t3)R”。此时旋转后的物体的坐标是R”’。

也就是说后一个操作是对当前物体的坐标进行操作。

那么我们两个两个看，联立前两个，先绕x轴t1角度再绕y轴t2角度，公式为R”=B(t2)R’=B(t2)A(t1)R。从公式中看这两步操作实际上是对R乘了两个矩阵B(t2)和A(t1)，这样就变成了R”。

注意，操作按照先后次序，右边的矩阵为先操作，左边的矩阵为后操作。

那么同理我们可以得到旋转三次后的坐标R”’=C(t3)B(t2)A(t1)R。

同理，如果存在多次操作，我们只需要按照顺序不断的左乘旋转矩阵就好。

不绕xyz轴旋转，过原点绕任意轴进行多次旋转
我们要将物体绕着直线z=y按右手方向旋转30度，这种情况就相对比较复杂了，因为它并不是xyz轴，所以我们旋转时有以下三步操作：

将坐标系进行旋转操作，令z=y

与原z轴重合，原z轴操作后的位置为z’轴；

将物体绕z轴按右手方向旋转30度；

将坐标系进行旋转操作，令z’轴与原z轴重合。

左边为原坐标系，右边为绕x轴旋转45度后的新坐标系，其中旋转过后的坐标系为xy’z’，我们想要绕着转的直线（原z=y）现在变成了z轴，那么这样子就变成了绕z轴旋转的情况。

所以我们将绕x轴旋转坐标系的操作记为A(45)，所以物体现在的坐标为R′=A(45)R

之后我们就可以将物体绕z轴右手方向旋转30度了，操作记为B(30)，所以现在物体的坐标为
R′′=B(30)R′

但是此时我们的坐标系还是以原z=y为z轴的坐标系，我们需要把z’轴转过来，变成最初的那个样子，所以我们需要把坐标系绕x轴旋转-45度，这样子z’就和z重合了，z=y也回到了原来的位置。

所以这一步操作记为A(-45)，物体现在的坐标为R”’=A(-45)R”。

最后总的来说，这个物体从最初的状态到最后的状态相当于进行了三步操作，乘上了三个矩阵，即R”’=A(-45)B(30)A(45)R.

围绕轴不经过原点的旋转-初级
上面的方法全部都要经过原点，但如果我们想要围着转的对称轴不经过原点呢？这就要多加一个操作了，那就是给坐标加上个某一个值，比如我有坐标向量(x, y, z)，想要向x轴平移1单位，那么新的坐标就变成了(x+1, y, z)，相当于进行了如下操作

(x’, y’, z’) = (x, y, z) + (1, 0, 0)

所以我们这里定义一个新操作D(a,x)。其中a代表沿着位移方向的轴，方向只有三个，xyz。x代表的是唯一的距离，比如说上述操作就可以写为D(x,1)，总的公式为R’=R+D(x,1)。

围绕轴不经过原点的旋转-高级
我们现在要将一个物体R绕着z=y-1这条线为轴右手方向旋转30度。其实步骤依旧和上面一模一样，只不过将z=y-1转到z轴上更为麻烦了而已，主要分为以下步骤。

首先将z=y-1平移到经过原点，也就是将坐标轴向y方向平移-1个单位，即操作D(y,1)，平移后的物体坐标为R’=R+D(y,-1)。

然后就是之前举的例子了，我们直接可以写得(我用R2代替R”，以此类推)

R2=A(45)R’

R3=B(30)R2

R4=A(-45)R3

最后到了这里我们还得把z=y-1移到原来位置，也就是再加上一个D(y,1)操作，也就是

R5=R4+D(y,-1)
=A(-45)B(30)A(45)[R+D(y,-1)]+D(y,1）

这样子，我们就可以实现任何操作

总结
可以看出，我们最终达到实现任何操作的步骤为三步

将我们想要旋转的轴通过旋转与平移操作将其与任一坐标轴重合；

进行我们想要绕着旋转轴旋转的操作；

将旋转轴通过旋转与平移操作移动到原来的位置。

并且我们的基础操作总共有4个，其中三个旋转一个平移，分别为：

绕x轴右手方向旋转t角度记为A(t);

绕y轴右手方向旋转t角度记为B(t);

绕z轴右手方向旋转t角度记为C(t);

沿某一轴(记为a轴)正方向平移x距离记为D(a, x)。

这样子我们得到的坐标就是我们实现了当前操作的坐标。