关于指数加权平均,已经有很多珠玉在前,很多博主都写了很好的博客。不过如果不自己推导消化一下,感觉东西就不是自己的,所以还是写个博客记录一下学习过程以及一些思考。
指数加权平均数学表达式
指数加权平均公式如下,其中 v t v_t vt为当前时刻平均值, v t − 1 v_{t-1} vt−1为上一时刻平均值, θ t \theta_t θt为当前时刻新数据, β \beta β小于1为权重系数。
v t = β v t − 1 + ( 1 − β ) θ t v_t=\beta v_{t-1}+(1-\beta)\theta_t vt=βvt−1+(1−β)θt
有的也写成如下形式,其中
α
=
1
−
β
\alpha=1-\beta
α=1−β,区别不大:
v
t
=
(
1
−
α
)
v
t
−
1
+
α
θ
t
v_t=(1-\alpha)v_{t-1}+\alpha\theta_t
vt=(1−α)vt−1+αθt
v
t
=
v
t
−
1
+
α
(
θ
t
−
v
t
−
1
)
v_t=v_{t-1}+\alpha(\theta_t-v_{t-1})
vt=vt−1+α(θt−vt−1)
按照上述计算方式,则:
v
0
=
0
v_0=0
v0=0
v
1
=
(
1
−
β
)
θ
1
v_1=(1-\beta)\theta_1
v1=(1−β)θ1
v
2
=
β
v
1
+
(
1
−
β
)
θ
2
=
β
(
1
−
β
)
θ
1
+
(
1
−
β
)
θ
2
v_2=\beta v_{1}+(1-\beta)\theta_2 =\beta (1-\beta)\theta_1+(1-\beta)\theta_2
v2=βv1+(1−β)θ2=β(1−β)θ1+(1−β)θ2
v
3
=
β
v
2
+
(
1
−
β
)
θ
3
=
β
2
(
1
−
β
)
θ
1
+
β
(
1
−
β
)
θ
2
+
(
1
−
β
)
θ
3
v_3=\beta v_{2}+(1-\beta)\theta_3 =\beta^2 (1-\beta)\theta_1+\beta(1-\beta)\theta_2 +(1-\beta)\theta_3
v3=βv2+(1−β)θ3=β2(1−β)θ1+β(1−β)θ2+(1−β)θ3
…
v
t
=
(
1
−
β
)
(
θ
t
+
β
θ
t
−
1
+
β
2
θ
t
−
2
+
+
β
3
θ
t
−
3
+
.
.
.
)
v_t =(1-\beta)(\theta_t + \beta\theta_{t-1}+\beta^2 \theta_{t-2}+ +\beta^3\theta_{t-3}+...)
vt=(1−β)(θt+βθt−1+β2θt−2++β3θt−3+...)
指数加权平均原理及其物理意义
指数加权平均的计算结果 v t v_t vt可以看作是 1 / ( 1 − β ) 1/(1-\beta) 1/(1−β)个数据的平均值,假设 β = 0.9 \beta=0.9 β=0.9,即相当于计算10个数据的平均值。由此可知,如果 β \beta β越大,则平均的数据越多,加权平均值更平滑,时间延迟更严重。
在实际应用中,如果数据的采样时间间隔为 T {T} T,想对时间常数 τ \tau τ内的采样值进行平均,那么只需要设置 β \beta β满足 1 / ( 1 − β ) = τ / T 1/(1-\beta)=\tau/{T} 1/(1−β)=τ/T。
那么为什么指数平均可以看作是 1 / ( 1 − β ) 1/(1-\beta) 1/(1−β)个数据的平均值的平均值呢?
由于 β \beta β小于1,所以随着指数的增大, β n \beta^n βn越趋近于0,而一般认为当指数项衰减到 1 e \frac{1}{e} e1就可以忽略不计。设 ϵ = 1 − β \epsilon=1-\beta ϵ=1−β,由于当 ϵ − > 0 + \epsilon -> 0^+ ϵ−>0+时, ( 1 − ϵ ) 1 ϵ − > 1 e (1-\epsilon )^{\frac{1}{\epsilon}}->\frac{1}{e} (1−ϵ)ϵ1−>e1,因此
β 1 1 − β = 1 e \beta^{\frac{1}{1-\beta}}=\frac{1}{e} β1−β1=e1
即可以看作只有最近的 1 1 − β {\frac{1}{1-\beta}} 1−β1个数据项进行了平均。
这里更直观的理解,可以假设 1 1 − β = n {\frac{1}{1-\beta}}=n 1−β1=n,那么上述指数加权平均公式变为:
v t = n − 1 n v t − 1 + 1 n θ t v_t=\frac{n-1}{n} v_{t-1}+\frac{1}{n}\theta_t vt=nn−1vt−1+n1θt
从上述表达式,可以认为新的数据权重占 1 n \frac{1}{n} n1,上一次的平均值占 n − 1 n \frac{n-1}{n} nn−1。个人觉得这种表达方式更方便记忆和理解。
偏差修正
在前期没有达到 1 / ( 1 − β ) 1/(1-\beta) 1/(1−β)个数据的情况下,如果对前期的平均值有精度要求,则需要进行修正。通过将 v t v_t vt除以 ( 1 − β t ) (1-\beta^{t}) (1−βt)来修正指数加权平均的误差。
v t = β v t − 1 + ( 1 − β ) θ t ( 1 − β t ) v_t=\frac{\beta v_{t-1}+(1-\beta)\theta_t}{(1-\beta^{t})} vt=(1−βt)βvt−1+(1−β)θt
由于随着t增大, ( 1 − β t ) (1-\beta^{t}) (1−βt)会趋近于1,因此对后期的指数加权平均没有影响。
一阶低通滤波
从时域和频域的角度来看,指数加权平均实际上也是一阶低通滤波或者控制模型中一阶惯性环节。通过画波特图和幅频响应曲线,可以看到各频率的幅值情况及相位延迟情况。
转折频率如下,其中
α
=
1
−
β
\alpha=1-\beta
α=1−β。
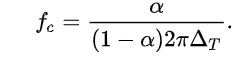
如果
β
=
0.9
\beta=0.9
β=0.9,采样频率0.01s,则转折频率1.7Hz。
参考来源
[1]优化算法之指数加权平均详解
[2] Moving average
[3] 一阶低通滤波(LPF)的原理及应用(以APM/PX4飞控为例)
[4] 指数加权平均





















 6244
6244











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








