第6章——深度学习入门（鱼书）

第6章 与学习相关的技巧

本章将介绍神经网络的学习中的一些重要观点，主题涉及 寻找最优权重参数的最优化方法、权重参数的初始值、超参数的设定方法 等。此外，为了应对过拟合，本章还将介绍 权值衰减、Dropout等正则化方法，并进行实现 。最后将对近年来众多研究中使用的 Batch Normalization 方法进行简单的介绍。使用本章介绍的方法，可以高效地进行神经网络（深度学习）的学习，提高识别精度。

6.1 参数的更新

神经网络的学习的目的是找到使损失函数的值尽可能小的参数 。这是寻找最优参数的问题，解决这个问题的过程称为 最优化（optimization） 。遗憾的是，神经网络的最优化问题非常难。这是因为参数空间非常复杂，无法轻易找到最优解（无法使用那种通过解数学式一下子就求得最小值的方法）。而且，在深度神经网络中，参数的数量非常庞大，导致最优化问题更加复杂。

在前几章中，为了找到最优参数，我们将参数的梯度（导数）作为了线索。使用参数的梯度，沿梯度方向更新参数，并重复这个步骤多次，从而逐渐靠近最优参数，这个过程称为 随机梯度下降法（stochastic gradient descent），简称SGD 。 SGD 是一个简单的方法，不过比起胡乱地搜索参数空间，也算是“聪明”的方法。但是，根据不同的问题，也存在比 SGD更加聪明的方法。本节我们将指出 SGD 的缺点，并介绍 SGD 以外的其他最优化方法。

6.1.1　探险家的故事

6.1.2　SGD

让大家感受了最优化问题的难度之后，我们再来复习一下 SGD 。用数学式可以将 SGD 写成如下的式（ 6 . 1 ）。

class SGD:
 def __init__(self, lr=0.01):
 self.lr = lr
 def update(self, params, grads):
 for key in params.keys():
 params[key] -= self.lr * grads[key]

这里，进行初始化时的参数 lr表示learning rate（学习率） 。这个学习率会保存为实例变量。此外，代码段中还定义了 update(params, grads) 方法，这个方法在 SGD 中会被反复调用。参数 params 和 grads （与之前的神经网络的实现一样）是字典型变量，按 params['W1'] 、 grads['W1'] 的形式，分别保存了权重参数和它们的梯度。

使用这个 SGD 类，可以按如下方式进行神经网络的参数的更新（下面的代码是不能实际运行的伪代码）。

network = TwoLayerNet(...)
optimizer = SGD()
for i in range(10000):
 ...
 x_batch, t_batch = get_mini_batch(...) # mini-batch
 grads = network.gradient(x_batch, t_batch)
 params = network.params
 optimizer.update(params, grads)
 ...

这里首次出现的变量名 optimizer 表示“进行最优化的人”（翻译为优化器可能更好）的意思，这里

由 SGD 承担这个角色。参数的更新由 optimizer 负责完成。我们在这里需要做的只是将参数和梯度的信息传给 optimizer 。

像这样，通过单独实现进行最优化的类，功能的模块化变得更简单。比如，后面我们马上会实现另一个最优化方法Momentum，它同样会实现成拥有update(params, grads)这个共同方法的形式。这样一来，只需要将optimizer = SGD()这一语句换成optimizer = Momentum()，就可以从SGD切

换为 Momentum 。

很多深度学习框架都实现了各种最优化方法，并且提供了可以简单切换这些方法的构造。比如 Lasagne深度学习框架，在 updates.py这个文件中以函数的形式集中实现了最优化方法。用户可以从中选择自己想用的最优化方法。

6.1.3　SGD的缺点

虽然 SGD 简单，并且容易实现，但是在解决某些问题时可能没有效率。这里，在指出 SGD 的缺点之际，我们来思考一下求下面这个函数的最小值的问题。

如图 6-1 所示，式（ 6 . 2 ）表示的函数是向 x 轴方向延伸的“碗”状函数。实际上，式（ 6 . 2 ）的等高线呈向 x 轴方向延伸的椭圆状。

6.1.4　Momentum

Momentum 是 “动量”的意思，和物理有关。用数学式表示 Momentum 方法，如下所示。

for key in params.keys():
 self.v[key] = self.momentum*self.v[key] - self.lr*grads[key]
 params[key] += self.v[key]

和前面的 SGD 一样， W 表示要更新的权重参数，表示损失函数关于 W 的梯度， η 表示学习率。这里新出现了一个变量 v ，对应物理上的速度。式（ 6 . 3 ）表示了物体在梯度方向上受力，在这个力的作用下，物体的速度增加这一物理法则。如图 6-4 所示， Momentum 方法给人的感觉就像是小球在地面上滚动。

式（ 6 . 3 ）中有 α v 这一项。在物体不受任何力时，该项承担使物体逐渐减速的任务（ α 设定为 0 . 9 之类的值），对应物理上的地面摩擦或空气阻力。下面是 Momentum 的代码实现（源代码在 common/optimizer.py 中）。

class Momentum:

    """Momentum SGD"""

    def __init__(self, lr=0.01, momentum=0.9):
        self.lr = lr
        self.momentum = momentum
        self.v = None
        
    def update(self, params, grads):
        if self.v is None:
            self.v = {}
            for key, val in params.items():                                
                self.v[key] = np.zeros_like(val)
                
        for key in params.keys():
            self.v[key] = self.momentum*self.v[key] - self.lr*grads[key] 
            params[key] += self.v[key]

实例变量 v 会保存物体的速度。初始化时， v 中什么都不保存，但当第一次调用 update() 时， v 会以字典型变量的形式保存与参数结构相同的数据。剩余的代码部分就是将式（ 6 . 3 ）、式（ 6 . 4 ）写出来，很简单。

现在尝试使用 Momentum 解决式（ 6 . 2 ）的最优化问题，如图 6-5 所示。

图 6-5 中，更新路径就像小球在碗中滚动一样。和 SGD 相比，我们发现“之”字形的“程度”减轻了。这是因为虽然 x 轴方向上受到的力非常小，但是一直在同一方向上受力，所以朝同一个方向会有一定的加速。反过来，虽然 y 轴方向上受到的力很大，但是因为交互地受到正方向和反方向的力，它们会互相抵消，所以 y 轴方向上的速度不稳定。因此，和 SGD 时的情形相比，可以更快地朝 x 轴方向靠近，减弱“之”字形的变动程度。

6.1.5　AdaGrad

在神经网络的学习中，学习率（数学式中记为η）的值很重要。学习率过小，会导致学习花费过多时间；反过来，学习率过大，则会导致学习发散而不能正确进行。

在关于学习率的有效技巧中，有一种被称为 学习率衰减 （ learning ratedecay ）的方法，即随着学习的进行，使学习率逐渐减小。实际上，一开始“多”学，然后逐渐“少”学的方法，在神经网络的学习中经常被使用。

逐渐减小学习率的想法，相当于将“全体”参数的学习率值一起降低。而 AdaGrad [6] 进一步发展了这个想法，针对“一个一个”的参数，赋予其“定制”的值。

AdaGrad 会为参数的每个元素适当地调整学习率，与此同时进行学习（ AdaGrad 的 Ada来自英文单词Adaptive，即“适当的”的意思 ）。下面，让我们用数学式表示 AdaGrad 的更新方法。

self.h[key] += grads[key] * grads[key]

params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)

和前面的 SGD 一样，W表示要更新的权重参数， 表示损失函数关于 W 的梯度， η 表示学习率。这里新出现了变量 h ，如式 (6 . 5) 所示，它保存了以前的所有梯度值的平方和（式（ 6 . 5 ）中的 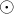表示对应矩阵元素的乘法）。然后，在更新参数时，通过乘以