海伯伦定理

谓词公式通过等价关系及推理规则化成相应的子句集

在谓词逻辑中，把原子谓词公式及其否定统称为文字。
定义3.5：任何文字的析取式称为子句。     例如： P(x)∨Q(x), ¬P(x,f(x))∨Q(x,g(x))
定义3.6：不包含任何文字的子句称为空子句。 空子句不含有文字，不能被任何解释满足，所以空子句是永假的，不可满足的。
任何谓词公式都可通过等价关系及推理规则化成相应的子句集。

1. 利用等价关系消去“→”和“↔”  ，例如公式

可等价变换成

2. 利用等价关系把“¬”移到紧靠谓词的位置上 ，上式经等价变换后

3. 重新命名变元，使不同量词约束的变元有不同的名字 ，上式经变换后

4. 消去存在量词
a.存在量词不出现在全称量词的辖域内，则只要用一个新的个体常量替换受该量词约束的变元，然后把存在量词删除。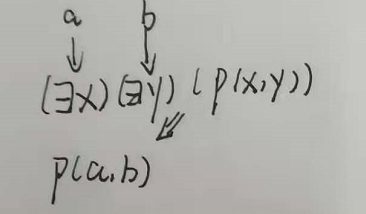
    
b.存在量词位于一个或者多个全称量词的辖域内，此时要用Skolem函数f(x1,x2,…,xn)替换受该存在量词约束的变元。     
上式中存在量词(y)及(z)都位于(x)的辖域内，所以需要用Skolem函数替换，设替换y和z的Skolem函数分别是f(x)和g(x)，则替换后得到

5. 把全称量词全部移到公式的左边
6. 利用等价关系把公式化为Skolem标准形

Skolem标准形的一般形式是

其中，M是子句的合取式，称为Skolem标准形的母式。     上式化为Skolem标准形后得到

7. 消去全称量词
8. 对变元更名，使不同子句中的变元不同名 上式化为


9. 消去合取词，就得到子句集

等价性

定理3.1： 设有谓词公式F，其标准形的子句集为S，则F不可满足性的充要条件是S不可满足。 所以： 如果要证明一个谓词公式是不可满足的，则只要证明其相应的子句集是不可满足的就可以了。

海伯伦域

判断一个子句的不可满足性，需要对个体域上的一切解释逐个进行判定，只有当子句对任何非空个体域上的任何一个解释都是不可满足的，该子句才是不可满足的。 海伯伦构造了一个特殊的域(海伯伦域)，并证明只要对这个特殊域上的一切解释进行判定，就可知子句集是否不可满足。

定义3.7 ：设S为子句集，则按下述方法构造的域H∞称为海伯伦域，记为H域。   
 (1)令H0是S中所有个体常量的集合，若S中不包含个体常量，则令H0＝{a}，其中a为任意指定的一个个体常量。   
 (2)令Hi+1=Hi∪{S中所有n元函数f(x1,…,xn)|xj(j=1,…,n)是Hi中的元素}，其中i=0,1,2,…。

例. 求子句集S={P(x)∨Q(x),R(f(y))}的H域。
解：此例中没有个体常量，任意指定一个常量a作为个体常量，得到
H0={a}
H1={a,f(a)}
H2={a,f(a),f(f(a))}
H3={a,f(a),f(f(a)),f(f(f(a)))}
…
H∞={a,f(a),f(f(a)),f(f(f(a))),…}