Reconstructing Clear Image for High-Speed Motion Scene With a Retina-Inspired Spike Camera 论文笔记

主要贡献

提出了一种分层运动对齐的时间滤波方案，将短期滤波与长期滤波相结合，利用了模型复杂度较低的长期时间相关性。

脉冲相机概述

脉冲相机原理

脉冲产生

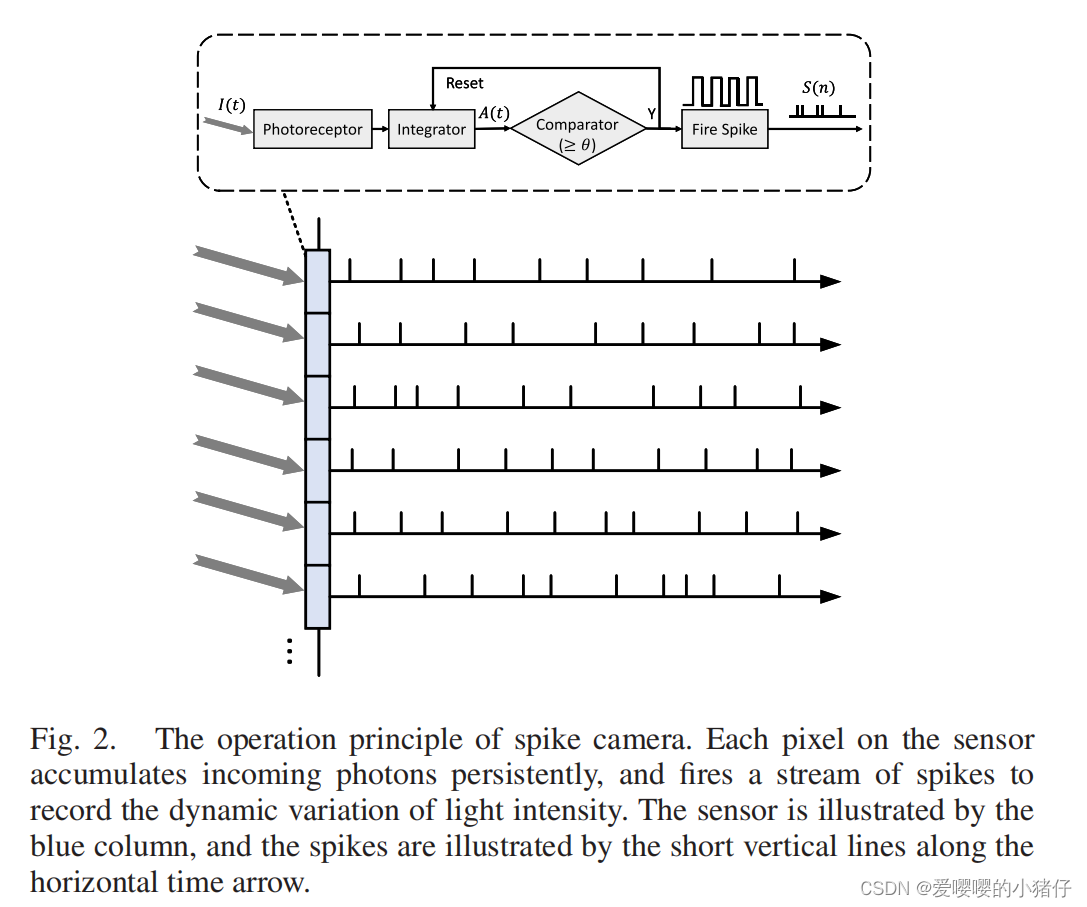
脉冲相机的机制如图2所示。该传感器由一组像素阵列构成，每一个像素都可以单独地记录光强。每一个像素都包含了三个主要部分：光感受器、积分器和比较器。光感受器捕捉环境中的光子，然后将瞬时光强$I(t)$转化为可以被积分器识别的电压。积分器累计电荷，比较器则检查所积累的信号：
$$A(t)={\int }_0^t\eta I(x)dx\text{\hspace{1em}(1)}$$
其中，$\eta$表示光电转化率。一旦积累的信号达到阈值$\theta$，像素建立flag信号并发出脉冲。同时立刻重置积分器，开始新一轮的“积累和发放”过程。这个信号累加过层可以表示为：
$$A(t)={\int }_0^t\eta I(x)dx\mathrm{mod}\theta \text{\hspace{1em}(2)}$$
在实际的电路设计中，脉冲由二值比特表示，并在时钟信号的控制下被读出。

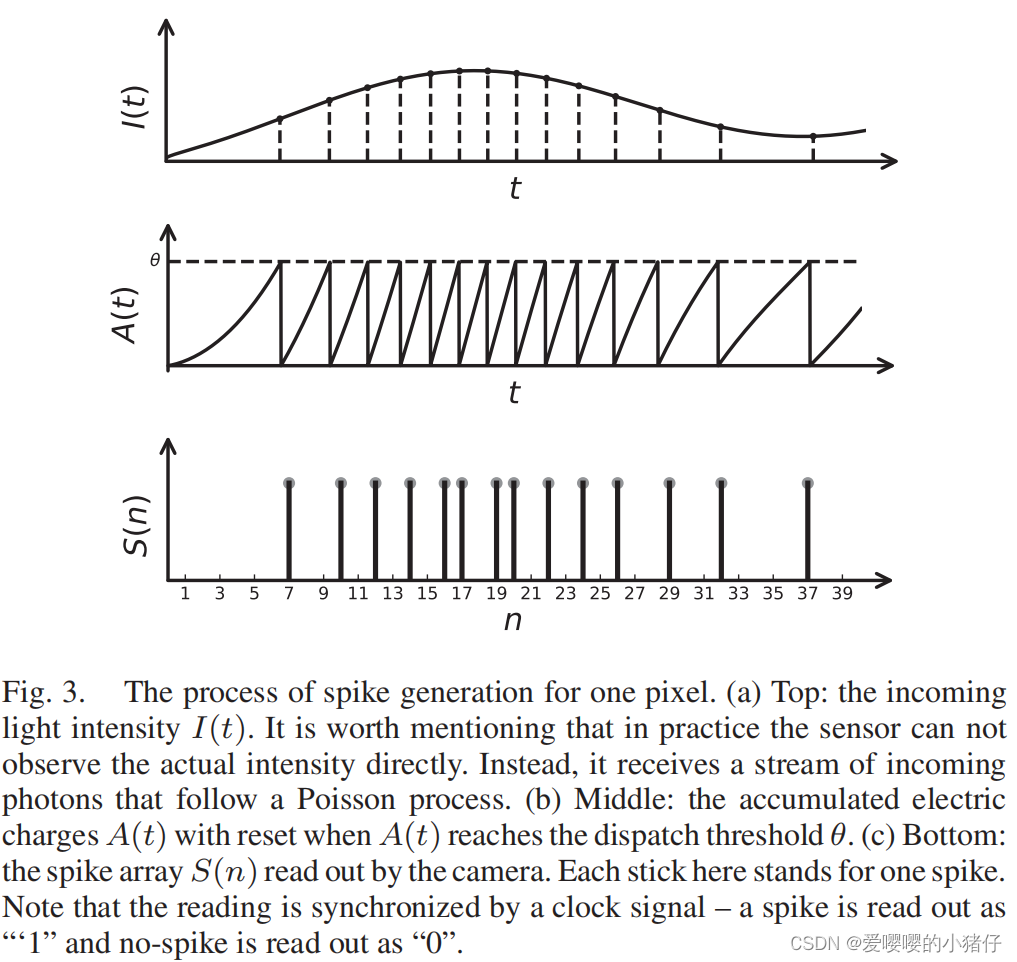
图三展示了电荷累计过程以及脉冲的产生，光强信号如图三(a)所示。我们从图3(b)中可以看到，信号$A(t)$重置为零的时间点正是产生脉冲的发射时间。这些点将工作周期划分为一组时间间隔，在每一个间隔内，信号$I(t)$积分为一个常数（如$\theta /\eta$），对应了一个脉冲的光子量。在当下的设计中，$\theta$由参考电压控制，可以更具不同的光照情况进行调整。

脉冲周期和脉冲间隙

由于每个像素独立工作，我们可以将我们的讨论限制在单一时刻的单一像素。假设 { t 1 , t 2 , t 3 , ⋅ ⋅ ⋅ } \{t_1,t_2,t_3,\cdot\cdot\cdot\} {t1​,t2​,t3​,⋅⋅⋅}是生成脉冲的发射时间，第$k$个脉冲的发射时间应该满足：
$${\int }_{t_{k-1}}^{t_k}\eta I(x)dx=\theta \text{\hspace{1em}(3)}$$
第$k$个脉冲开始于$t_{k-1}$结束于$t_k$。我们将这个间隔段叫做第$k$个脉冲的生命周期或者脉冲间隔。我们可以从图3中观察到脉冲频率随瞬时光强的变化。当光强强时，脉冲相机产生更短脉冲间隔的密集脉冲流。当光强弱时，脉冲相机产生更长脉冲间隔的稀疏脉冲流。

脉冲的读出

脉冲图像传感器上的相似可以在任意时间发射脉冲，但是相机只能以离散二值信号$S(n)$的形式读出脉冲。相机周期性地检查flag标志，在时间$t=nT,n=1,2,...$，其中$T$表示固定的时间间隔。如果flag在$t=nT$时被置位，脉冲相机读出$S(n)=1$并且清除flag标志，以备下一个脉冲的到来。第$k$个在$t_k$时间被读出为$S(n_k)=1$的脉冲满足下式：
$$n_k=\lceil t_k/T\rceil$$
因此，$S(n)$的指数$n$是连续时间$t$的离散近似。为了保持每个脉冲的时间信息尽可能准确，读出间隔$T$应该足够小。

脉冲数据格式

相机使用了一个高速池化操作来周期性地检查每个像素的状态。在目前的实现中，相机每秒检查$40000$次。每次检查，它针对每个像素都会读出一个flag（0或者1），最终形成一个$H\times W$的脉冲帧。二值的帧通过简单的方式被压缩，然后通过高速数据接口发射。随着时间的推移，相机产生三维的$H\times W\times N$脉冲块$S(x,y,n)$，如图1(a)所示。为了后续讨论的方便，我们使用$S_n(z)$来表示脉冲帧，其中$n$是时间索引，$z=(x,y)$是像素坐标。

针对脉冲相机的光强推测

脉冲相机的目的是记录高速移动场景下的动态光强变化。一旦脉冲帧阵列被捕捉，我们旨在恢复任意时刻的瞬时光强$I_n(z)$。

基于时间间隔的推测

一个推测光强的方法时考虑每个脉冲的生命周期。一定量的电荷在这个周期被积累。因此，我么可以从脉冲的时间间隔来推测光照强度。

以像素$z$为和时间索引$n$为例。覆盖点$(z,n)$的脉冲周期的起始时间可以计算为：
P ( z , n ) = max ⁡ { k ∣ S k ( z ) = 1 , k < n } N ( z , n ) = min ⁡ { k ∣ S k ( z ) = 1 , k ≥ n } \begin{align} P(z,n)=\max\{k|S_k(z)=1,k<n\}\tag{5} \\ N(z,n)=\min\{k|S_k(z)=1,k≥n\}\tag{6} \end{align} P(z,n)=max{k∣Sk​(z)=1,k<n}N(z,n)=min{k∣Sk​(z)=1,k≥n}​(5)(6)​
由于一个脉冲周期通常持续很短的时间，我们可以假设光强在这段时间内不变，根据公式(3)中的脉冲产生模型，我们有：
$$\eta I_n(z)\cdot [N(z,n)-P(z,n)]\cdot T+{ϵ}_n(z)\approx \theta \text{\hspace{1em}(7)}$$
这里我们用小的随机扰动${ϵ}_k(z)$来表示由暗电流或者到达光子泊松效应造成的噪声。我们在公式(7)中使用约等于号是因为离散时间索引$n_k$只是真实脉冲激发时间$t_k$的近似，如公式(4)所示。基于公式(7)，瞬时光强可以被表达为：
$${\hat{I}}_n(z)=\frac{\theta }{\eta T[N(z,n)-P(z,n)]}\text{\hspace{1em}(8)}$$

挑战

上述的基于时间间隔的方法本质上是基于瞬时光强的重建方法。图4(a)展示了根据公式(8)得到的图像重建结果。可以发现得到的图像非常嘈杂。这是因为瞬时光强其实很难准确衡量。事实上，即使在很定光照下，短时间到达的光子数量是一个满足泊松分布的随机变量。另一个可能会导致嘈杂重建的因素是由于对$t_k$的离散近似，导致对脉冲时间间隔的估计不准确。

为了抑制噪声的影响，一个直观的方法是联合地考虑多个脉冲周期接受到的光子。在这种情况下，估计变为：
$$\widehat{I_n}(z)=\frac{(2m-1)\cdot \theta }{\eta T[N^{(m)}(z,n)-P^{(m)}(z,n)]}\text{\hspace{1em}(9)}$$
其中
P ( m ) ( z , n ) = max ⁡ { k ∣ ∑ i = k n − 1 S i ( z ) = m , k < n } N ( m ) ( z , n ) = min ⁡ { k ∣ ∑ i = n k S i ( z ) = m , k ≥ n } \begin{align} P^{(m)}(z,n)=\max\{k|\sum_{i=k}^{n-1}S_i(z)=m,k<n\}\tag{10} \\ N^{(m)}(z,n)=\min\{k|\sum_{i=n}^{k}S_i(z)=m,k≥n\}\tag{11} \end{align} P(m)(z,n)=max{k∣i=k∑n−1​Si​(z)=m,k<n}N(m)(z,n)=min{k∣i=n∑k​Si​(z)=m,k≥n}​(10)(11)​
其中$2m$是脉冲数，$N^{(m)}(z,n)-P^{(m)}(z,n)$是$2m-1$个脉冲周期的长度。图4(b)给出了使用公式(9)重建出的图像，其中$m=5$。通过在多个脉冲周期内平均光子，静态场景中扰动${ϵ}_k(n)$的影响会被极大程度上抑制，产生更好的重建结果。但是，对于高速运动的动态场景，物体的运动导致了如图4(b)所示的运动模糊。所以当物体快速移动时，简单地沿着时间轴方向对光子进行平均是不合适的。

基于运动对齐的脉冲相机图像重建

正如我们所讨论的，高速场景下的成像非常具有挑战性。光子的积累可以抑制传感器噪声的影响，但是高速运动的存在导致了来自不同物体点的光线融合（运动模糊）。为了解决这个问题，我们提出了基于运动对齐的光强推测方法。具体来说，我们提出了基于运动对齐的时间滤波机制，来探索沿着运动轨迹的光线时间关联性。

总体框架

我们打算从记录的脉冲数据$S$中恢复任意时刻，质量尽可能高的光照强度$I$。考虑的物体的运动，探索沿着运动轨迹的时间关联性非常有必要，这样就可以在获得高质量重建的同时不引入运动模糊。为了这个目的，我们提出了基于运动对弈的重建框架，如图5所示。

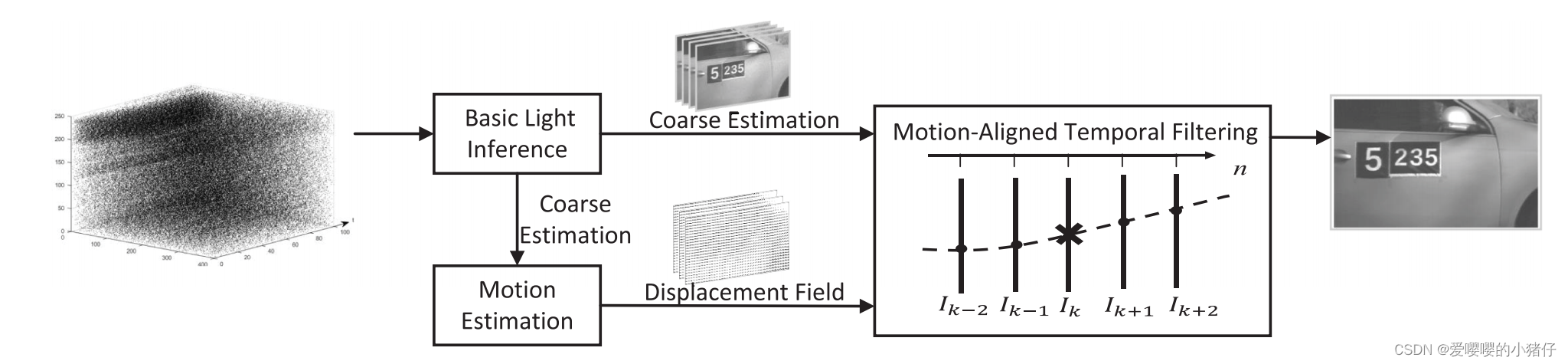
假设$I_k$是带重建的关键帧，我么首先通过公式(8)推测不同时刻的瞬时光强，产生一系列的初始估计$\widehat{I_n},n=1,2,...$。然后，我们基于这些初步估计得到的重建图像，生成关键帧和一系列相邻帧之间运动场 { u k → k + i } \{u_{k\rightarrow k+i}\} {uk→k+i​}。最终，基于这些运动场，基于运动对齐的时间滤波器被用来优化这些初始估计，产生最终高质量的重建图像${\overline{I}}_k$。

运动估计

为了探索时间相关性来减少噪声的影响，同时不引入运动模糊，我们需要找到通过每一个打算重建像素的运动轨迹，然后关键帧${\hat{I}}_k$上的像素就可以被投影到相邻的参考帧 { I ^ k + i } , i = ± 1 , ± 2 , . . . \{\hat{I}_{k+i}\},i=±1,±2,... {I^k+i​},i=±1,±2,...。这个问题可以通过光流解决。在本文中，我们使用了最经典的光流估计算法。具体来说，我们嘉定沿着运动轨迹的光照强度恒定，运动平滑，于是有了下面的优化方程：
$$\underset{u_{k\to k+i}}{\min }|\nabla u_{k\to k+i}{|}_2^2+\eta |{\hat{I}}_{k+i}(z+u_{k\to k+i}(z))-{\hat{I}}_k(z){|}_2^2\text{\hspace{1em}(12)}$$
其中$\eta$是光照一致性和平滑正则项的权衡系数。使用了欧拉-拉格朗日方程解决这个问题后，我们便得到了将$I_k$中像素投影到$I_{k+i}$像素中的运动场。

基于运动对齐的时间滤波

值得注意的，对整个图像使用一个固定的滤波器进行处理很难有效时间关联性。一方面，由于场景内容的多样性，沿着运动轨迹的时间相关性可能会在不同的像素位置之间发生显著的变化。另一方面，由于物体遮挡以及光照变化的存在，在一些情况下光照一致性假设难以满足。当外点出现在运动轨迹上时，他们需要被区别对待。

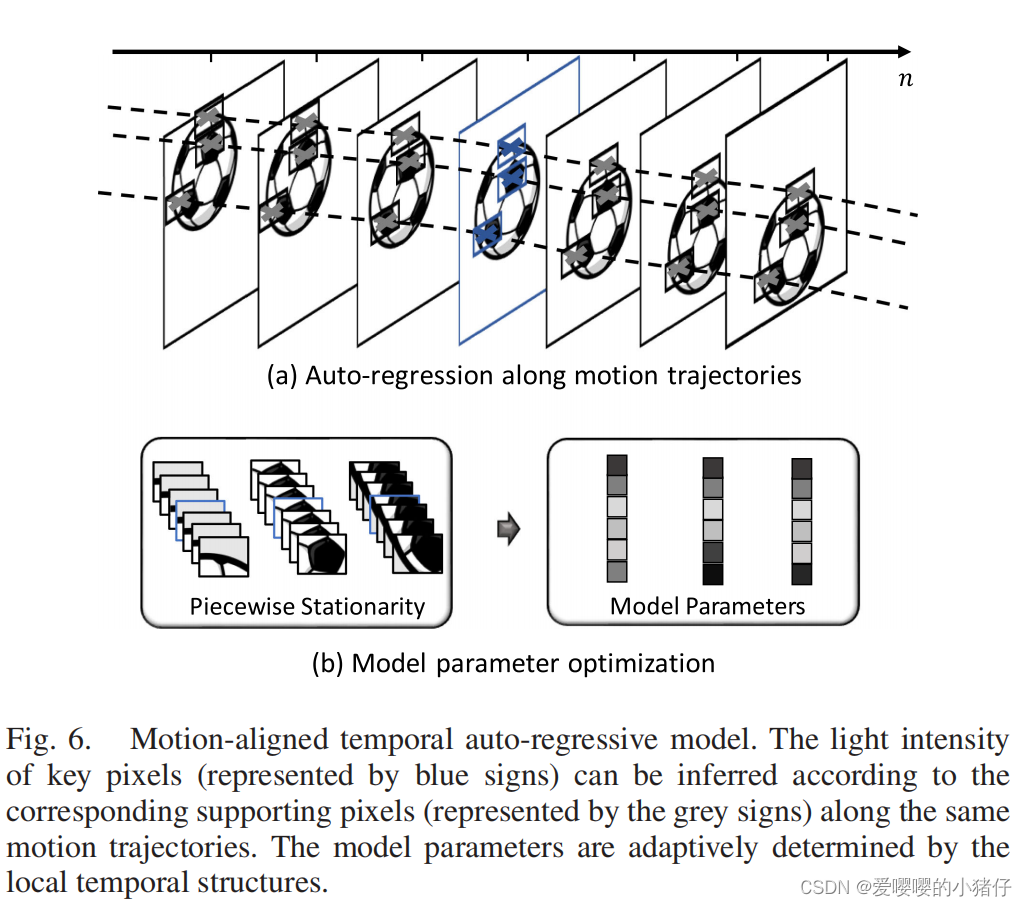
为了自适应地处理沿着运动轨迹的时间相关性，我们使用了自回归（AR, auto-regressive）模型。

1）时间自回归（TAR, temporal auto-regressive）模型：为了表征脉冲阵列之间的时间相关性，可以将光强建模为一个沿着运动轨迹的自回归过程，如图6所示。可以表示为：
$$I_k(z)=\sum _{i\in \varphi }{\alpha }_i{I}_{k+i}(z+u_{k\to k+i}(z))+\epsilon \text{\hspace{1em}(13)}$$
其中，$\varphi$是一个时间指数偏移量的模板，表示自回归模型的时间依赖结构。一个典型的$\varphi$选择方式为 { ± 1 , ± 2 , . . . , ± K } \{±1,±2,...,±K\} {±1,±2,...,±K}。 { α i } \{\alpha_i\} {αi​}是一系列的权重系统。$\epsilon$是独立于时空位置的扰动，包含了图像信息的细节信息和随机噪声。

TAR模型的有效性取决于自适应地调整模型参数${\alpha }_i$以反映视觉信号的局部时间相关结构的机制。假设运动和光强的变化是局部平滑的，这表明了分段平稳性。换句话说，参数${\alpha }_i$在一个小的区域内几乎保持不变，尽管它们可能在不同的区域有显著的变化。这种分段平稳性使得通过将局部窗口内的光强样本拟合到TAR模型中来学习信号结构成为可能。基于学习到的结构，我们可以利用时间相关性来生成质量更好的重建图像。

2）空间自适应时间滤波：假设$I_k$是我们打算重建的图像，$z$是任意的像素。在运动场 { u k → k + i } \{u_{k\rightarrow k+i}\} {uk→k+i​}的帮助下，我们使用TAR模型，沿着运动轨迹对初始估计的亮度进行滤波，得到更加稳定的重建图像：
$${\overline{I}}_k(z)=\sum _{i\in \varphi }{\alpha }_i{\hat{I}}_{k+i}(z+u_{k\to k+i}(z))\text{\hspace{1em}(14)}$$
值得注意的是公式(14)中的$u_{k\to k+i}(z)$可以是亚像素的运动场。为了获得亚像素的位置的光照强度${\hat{I}}_{k+i}(z+u_{k\to k+i}(z))$，可以使用诸如双边插值、NEDI和SAI的插值方法。

基于分段平稳性的假设，通过求解下面的最小二乘问题，$I_k$中$z$位置的TAR模型参数$\alpha$可以适应信号的局部结构：
$$\arg \underset{\alpha }{\min }\sum _{z^{\prime }\in {\Omega }_z}(I_k(z^{\prime })-\sum _{i\in \varphi }{\alpha }_i{I}_{k+i}(z^{\prime }+u_{k\to k+i}(z^{\prime })){)}^2\text{\hspace{1em}(15)}$$
当然，真实信号$I_k$无法获得，我们使用${\hat{I}}_k$进行替代求解公式(15)。这里，${\Omega }_z$是像素$z$附近的二维局部窗口。通常来说，${\Omega }_z$的尺寸，也就是窗口包含的临近像素数量，会被设置的远大于$\varphi$的长度，从而保证上述问题的有效解决并且避免过拟合。

局限性

为了充分利用时间相关性来提高重建质量，应采用沿长运动轨迹结合信号的长期TAR模型。这方面对于我们的高速脉冲相机的情况特别重要，因为它的采样率高达40000Hz。然而，随着$\varphi$尺寸的增加，TAR模型的复杂性也随之增加，引入了大量的参数 { α i } \{α_i\} {αi​}。如之前所述，为了获得 { α i } \{α_i\} {αi​}的可靠估计，应该相应地增加窗口$\Omega$。然而，TAR模型的有效性依赖于局部空间窗口内的时间相关结构接近恒定的分段平稳性。如果$\Omega$的尺寸太大，平稳性假设就不再成立，这将影响TAR模型的精度。

基于运动估计的多层级时间滤波

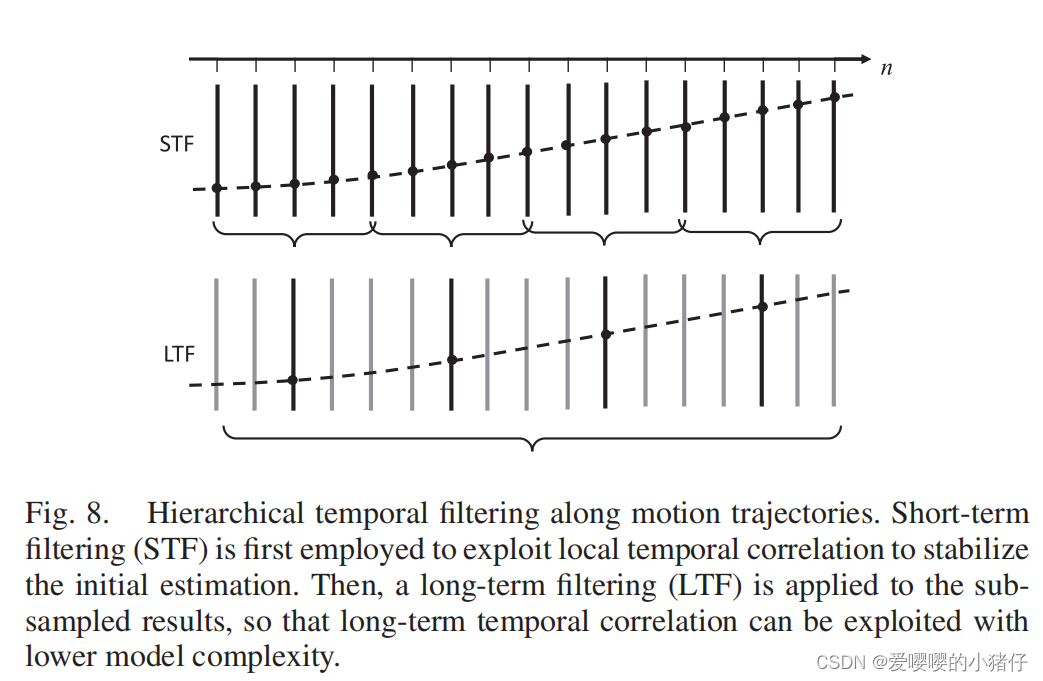
为了解决针对长轨迹的TAR模型学习问题，我们提出了多层级时间自回归模型。基于此，我们提出了基于运动估计的多层级时间滤波（MAHTF, motion-aligned hierarchical temporal filtering）框架，如图7所示。它采用了如图8所示的层级滤波结构，可以首先使用短期滤波（STF, short-term filtering），然后使用降低模型自由度的长期滤波（LTF, long-term filtering）。通过这样的方式，长期时间相关性可以在保证不过拟合的情况下被获得。

总览

整体框架如图7所示。为了实现高质量的常见，我们分三个阶段，通过由粗到细的方式来恢复视觉场景。假设$I_k$是我们准备重建的帧。首先，通过公式(8)得到 { I k + i } \{I_{k+i}\} {Ik+i​}的初始估计 { I ^ k + i } \{\hat{I}_{k+i}\} {I^k+i​}，其中$i=0,\pm 1,\pm 2,...$。然后得到${\hat{I}}_k$和${\hat{I}}_{k+i}$之间的运动估计，得到运动场$u_{k\to k+i}$，其中$i=\pm 1,\pm 2,...$。假设视觉场景在短时间内通常不会有剧烈变化，一个基于运动对齐的STF被使用在 { I ^ k ± i } \{\hat{I}_{k±i}\} {I^k±i​}上，从而探究其短期时间相关性，并且减少接下来的长期TAR模型的自由度。STF会产生一系列更细致的估计 { I ~ k ± i } \{\tilde{I}_{k±i}\} {I~k±i​}。最终，为了进一步细化重建，运动估计被用来细化运动场，基于运动估计的LFT被用在 { I ~ k ± i } \{\tilde{I}_{k±i}\} {I~k±i​}上。TAR模型根据局部内容结构自适应地调整模型参数。特别是，由于STF已经利用了短期相关性，我们建立了基于时间子采样的长期TAR模型。这种设计有助于降低TAR模型的复杂性，但它不影响长期时间相关性的利用。

短期滤波

我们使用短期滤波来探索短时间内的相关性，并且降低长期相关TAR模型的自由度。在本文中，短期被定义为非常短的时间，例如几个脉冲采样点（0.1∼0.2ms）。一般来说，自然图像信号在短期内沿着运动轨迹通常表现出很强的时间相关性，且相关结构趋于相同，STF可以使用一个固定的滤波器，$I_k(z)$可以表达为：
$${\tilde{I}}_k(z)=\frac{1}{C}\sum _{i=-r_s}^{r_s}{\omega }_i\cdot {\hat{I}}_{k+i}(z+u_{k\to k+i}(z))\text{\hspace{1em}(16)}$$
这里，$r_s$是短期滤波的半径，$C=\sum {\omega }_i$是归一化因子。基于广泛应用的马尔科夫模型，视觉信号的时间相关性强度随时间距离的增加而衰减。因此，我们对于STF我们使用了相对简单的滤波器，滤波器的权重可以表示为：
$${\omega }_i=e^{-\frac{i^2}{2{\delta }^2}}\text{\hspace{1em}(17)}$$
这里，$\delta$由半径$r_s$决定。

长期滤波

我们采用基于 { I ~ n } \{\tilde{I}_n\} {I~n​}的长期滤波，在长时间内利用时间相关性。为了自适应地利用这种相关性，我们建立了一个沿着运动轨迹的TAR模型。具体来说，由于短期相关性已经通过STF被利用，本文在建立长时自回归模型时进行了时间方向上的下采样，如图8所示。该模型从几个具有固定帧间隔的估计帧中得出$I_k(z)$的最终估计值：
$${\overline{I}}_k(z)=\sum _{i=-r_l}^{r_l}{\alpha }_i\cdot {\tilde{I}}_{k+i\cdot \overline{T}}(z+u_{k\to k+i\cdot \overline{T}}(z))\text{\hspace{1em}(18)}$$
其中，$r_l$表示TAR模型的半径， { α i } \{\alpha_i\} {αi​}是一系列的滤波器权重，可以根据信号结构进行自适应的调整。$\overline{T}$表示LTF的采样间隔。相比于公式(14)所描述的时域自回归模型，取同样的时域窗口，该模型的复杂度明显更低。如图6所示，长期滤波权重可以根据信号结构自适应的调节。此外，为了避免过拟合，本文额外增加了一个正则项来约束长期滤波参数的自由度。因此，长期滤波的权重可以通过下面的式子确定：
$$\arg \underset{\alpha }{\min }\eta ||\alpha |{|}_2^2+\sum _{z^{\prime }\in {\Omega }_z}({\tilde{I}}_k(z^{\prime })-\sum _{-r_l}^{r_l}{\alpha }_i{\tilde{I}}_{k+i\cdot \overline{T}}(z^{\prime }){)}^2\text{\hspace{1em}(19)}$$
其中，${\Omega }_z$表示以点$z$为中心的空域窗口。

计算复杂度

为了加快算法的速度，我们使用STF作为预处理，预处理的复杂性为$O(n)$。然后，主要的计算复杂度是关于运动对齐和LTF滤波权值 { α i } \{α_i\} {αi​}的参数估计。运动对齐的复杂性与LTF中使用的帧数$2r_l$成正比。滤波权重计算的复杂度与窗口大小和空间重叠程度有关。由于LTF通过求解式(19)来确定一个块的滤波数，块越大，重叠越小，算法运行速度越快。然而，较大的块尺寸可能会降低TAR模型的适应性。因此，需要在算法的复杂度和模型的精度之间进行权衡。假设每个图像被划分为$m$个块，重建$n$个图像的时间复杂度为$O(n\times m+n\times 2r_l)$。

实验