目录
1. 基本概念
在前馈神经网络中,信息的传递是单向的,这种限制虽然使得网络变得更容易学习,但在一定程度上也减弱了神经网络模型的能力。前馈神经网络可以看作一个复杂的函数,每次输入都是独立的,即网络的输出只依赖于当前的输入。但是在很多现实任务中,网络的输出不仅和当前时刻的输入相关,也和其过去一段时间的输出相关。比如一个有限状态自动机,其下一个时刻的状态(输出)不仅仅和当前输入相关,也和当前状态(上一个时刻的输出)相关。此外,前馈网络难以处理时序数据,比如视频、语音、文本等。时序数据的长度一般是不固定的,而前馈神经网络要求输入和输出的维数都是固定的,不能任意改变。因此,当处理这一类和时序数据相关的问题时,就需要一种能力更强的模型。
循环神经网络(Recurrent Neural Network,RNN)是一类具有短期记忆能力的神经网络。在循环神经网络中,神经元不但可以接受其他神经元的信息,也可以接受自身的信息,形成具有环路的网络结构。和前馈神经网络相比,循环神经网络更加符合生物神经网络的结构。循环神经网络已经被广泛应用在语音识别、语言模型以及自然语言生成等任务上。循环神经网络的参数学习可以通过随时间反向传播算法来学习。随时间反向传播算法即按照时间的逆序将错误信息一步步地往前传递。
当输入序列比较长时,会存在梯度爆炸和消失问题,也称为长程依赖问题。为了解决这个问题,人们对循环神经网络进行了很多的改进,其中最有效的改进方式引入门控机制(Gating Mechanism)。
为了处理这些时序数据并利用其历史信息, 我们需要让网络具有短期记忆能力。一般来讲,我们可以通过以下三种方法来给网络增加短期记忆能力:
(1)延时神经网络
一种简单的利用历史信息的方法是建立一个额外的延时单元,用来存储网络的历史信息(可以包括输入、输出、隐状态等)。比较有代表性的模型是延时神经网络(Time Delay Neural Network,TDNN)。
延时神经网络是在前馈网络中的非输出层都添加一个延时器,记录神经元的最近几次活性值。在第 个时刻,第
层神经元的活性值依赖于第
层神经元的最近
个时刻的活性值,即:

其中 表示第
层神经元在时刻
的活性值。通过延时器,前馈网络就具有了短期记忆的能力。
延时神经网络在时间维度上共享权值,以降低参数数量.因此对于序列输入来讲,延时神经网络就相当于卷积神经网络。
(2)有外部输入的非线性自回归模型
自回归模型(AutoRegressive Model,AR)是统计学上常用的一类时间序列模型,用一个变量 的历史信息来预测自己:

其中 为超参数,
,……,
为可学习参数,
为第
个时刻的噪声,方差
和时间无关。
有外部输入的非线性自回归模型(Nonlinear AutoRegressive with Exogenous Inputs Model,NARX)是自回归模型的扩展,在每个时刻 都有一个外部输入
,产生一个输出
,NARX通过一个延时记录最近
次的外部输入和最近
次的输出,第
个时刻的输出
为:
![]()
其中 表示非线性函数,可以是一个前馈网络,
和
为超参数。
(3)循环神经网络
循环神经网络(Recurrent Neural Network,RNN)通过使用带自反馈的神经元,能够处理任意长度的时序数据。给定一个输入序列 ,循环神经网络通过下面公式更新带反馈边的隐藏层的活性值
:
其中 ,
表示非线性函数,可以是一个前馈网络。从数学上讲,上面公式可以看成一个动力系统。因此,隐藏层的活性值在很多文献上也称为状态(State)或隐状态(Iidden State)。
动力系统(Dynamical System)的概念,指系统状态按照一定的规律随时间变化的系统。具体地讲,动力系统是使用一个函数来描述一个给定空间(如某个物理系统的状态空间)中所有点随时间的变化情况。生活中很多现象(比如钟摆晃动、台球轨迹等)都可以动力系统来描述。
下图给出了循环神经网络的示例,其中“延时器”为一个虚拟单元,记录神经元的最近一次的活性值:

由于循环神经网络具有短期记忆能力,相当于存储装置,因此其计算能力十分强大。理论上,循环神经网络可以近似任意的非线性动力系统。前馈神经网络可以模拟任何连续函数,而循环神经网络可以模拟任何程序。
2. 简单循环网络
2.1 简单循环网络
简单循环网络(Simple Recurrent Network,SRN)是一个非常简单的循环神经网络,只有一个隐藏层。在一个两层的前馈神经网络中,连接存在于相邻的层与层之间,隐藏层的节点之间是无连接的。而简单循环网络增加了从隐藏层到隐藏层的反馈连接。
令向量 表示在时刻
时网络的输入,
表示隐藏层状态(即隐藏层神经元活性值),则
不仅和当前时刻的输入
有关,也和上一时刻的隐藏层状态
相关。简单循环网络在时刻
的更新公式为:
式中: 为状态-状态权重矩阵,用于连接上一时间步的隐藏状态到当前时间步的隐藏状态;
为状态-输入权重矩阵,用于连接当前时间步的输入到隐藏状态;
为偏置向量;
表示非线性激活函数,通常为Logistic函数或Tanh函数。
2.2 长程依赖问题
(1) 长程依赖问题
循环神经网络在学习过程中的主要问题是由于梯度消失或爆炸问题,很难建模长时间间隔(Long Range)的状态之间的依赖关系。
梯度消失:是指随着网络层数的增加,反向传播过程中梯度值逐渐减小到几乎为零的现象。这意味着靠近输入层的权重几乎不会得到有效的更新,从而导致这些层的学习速度非常慢或者根本不学习。
梯度爆炸:是指在反向传播过程中,梯度值变得异常大,导致权重更新幅度过大,模型参数可能发散,使得训练过程变得不稳定。
虽然简单循环网络理论上可以建立长时间间隔的状态之间的依赖关系,但是由于梯度爆炸或消失问题,实际上只能学习到短期的依赖关系。这样,如果时刻 的输出
依赖于时刻
的输入
,当间隔
比较大时,简单神经网络很难建模这种长距离的依赖关系,称为长程依赖问题(Long-Term Dependencies Problem)。
(2) 解决方案
为了避免梯度爆炸或消失问题,一种最直接的方式就是选取合适的参数,同时使用非饱和的激活函数,但这种方式需要足够的人工调参经验,限制了模型的广泛应用。比较有效的方式是通过改进模型或优化方法来缓解循环网络的梯度爆炸和梯度消失问题。
梯度爆炸问题:循环网络的梯度爆炸问题比较容易解决,一般通过权重衰减或梯度截断来避免:
- 权重衰减是通过给参数增加
或
范数的正则化项来限制参数的取值范围;
- 梯度截断是设置一定阈值,当梯度的模大于一定阈值时,就将它截断成为一个较小的数。
梯度消失问题:梯度消失是循环网络的主要问题。除了使用一些优化技巧外,更有效的方式就是改变模型,比如:
这样, 和
之间既有线性关系,也有非线性关系,且缓解了梯度消失问题。但这种改进依然存在两个问题:梯度爆炸问题和记忆容量问题。
- 记忆容量(Memory Capacity)问题:随着
不断累积存储新的输入信息,会发生饱和现象,也就是说,隐藏状态
可以存储的信息是有限的,随着记忆单元存储的内容越来越多,其丢失的信息也越来越多。
为了解决这两个问题,可以通过引入门控机制来进一步改进模型(第5节)。
3. 循环神经网络的模式与参数学习
3.1 循环神经网络的模式
根据应用到不同类型的机器学习任务,循环神经网络可以分为以下几种模式:序列到类别模式、同步的序列到序列模式、异步的序列到序列模式。
(1)序列到类别模式
序列到类别模式主要用于序列数据的分类问题:输入为序列,输出为类别。比如在文本分类中,输入数据为单词的序列,输出为该文本的类别。
假设一个样本 为一个长度为
的序列,输出为一个类别
。我们可以将样本
按不同时刻输入到循环神经网络中,并得到不同时刻的隐藏状态
。我们可以将
看作整个序列的最终表示(或特征),并输入给分类器
进行分类,即:
其中 可以是简单的线性分类器(比如Logistic回归)或复杂的分类器(比如多层前馈神经网络)。
除了将最后时刻的状态作为整个序列的表示之外,我们还可以对整个序列的所有状态进行平均,并用这个平均状态来作为整个序列的表示,即:
(2)同步的序列到序列模式
同步的序列到序列模式主要用于序列标注(Sequence Labeling)任务,即每一时刻都有输入和输出,输入序列和输出序列的长度相同。比如在词性标注(Part-of-Speech Tagging)中,每一个单词都需要标注其对应的词性标签。
在同步的序列到序列模式中,输入为一个长度为 的序列
,输出为序列
。样本
按不同时刻输入到循环神经网络中,并得到不同时刻的隐状态
。每个时刻的隐状态
代表了当前时刻和历史的信息,并输入给分类器
得到当前时刻的标签
,即:
(3)异步的序列到序列模式
异步的序列到序列模式也称为编码器-解码器(Encoder-Decoder)模型,即输入序列和输出序列不需要有严格的对应关系,也不需要保持相同的长度。比如在机器翻译中,输入为源语言的单词序列,输出为目标语言的单词序列。
在异步的序列到序列模式中,输入为长度为 的序列
,输出为长度为
的序列
。异步的序列到序列模式一般通过先编码后解码的方式来实现。先将样本
按不同时刻输入到一个循环神经网络(编码器)中,并得到其编码
,然后再使用另一个循环神经网络(解码器),得到输出序列
。为了建立输出序列之间的依赖关系,在解码器中通常使用非线性的自回归模型。令
和
分别为用作编码器和解码器的循环神经网络,则编码器-解码器模型可以写为:

其中, 为分类器,
为预测输出
的向量表示。
在解码器中通常采用自回归模型,每个时刻的输入为上一时刻的预测结果 。
3.2 参数学习
循环神经网络的参数可以通过梯度下降方法来进行学习。
循环神经网络中存在一个递归调用的函数 ,因此,其计算参数梯度的方式和前馈神经网络不太相同。在循环神经网络中主要有两种计算梯度的方式:随时间反向传播(BPTT)算法和实时循环学习(RTRL)算法。
(1)随时间反向传播算法
随时间反向传播(BackPropagation Through Time,BPTT)算法的主要思想是通过类似前馈神经网络的误差反向传播算法来计算梯度。
BPTT算法将循环神经网络看作一个展开的多层前馈网络,其中“每一层”对应循环网络中的“每个时刻”。这样,循环神经网络就可以按照前馈网络中的反向传播算法计算参数梯度。在“展开”的前馈网络中,所有层的参数是共享的,因此参数的真实梯度是所有“展开层”的参数梯度之和。
关于BPTT算法的原理,可参看下文这篇文章:
随时间反向传播(BackPropagation Through Time,BPTT) https://www.cnblogs.com/shixiangwan/p/9289862.html
https://www.cnblogs.com/shixiangwan/p/9289862.html
(2)实时循环学习算法
实时循环学习(Real-Time Recurrent Learning, RTRL)算法是一种用于训练循环神经网络的方法,尤其是在训练长序列数据时。与反向传播的BPTT算法不同的是,RTRL算法是通过前向传播的方式来计算梯度。
RTRL算法的主要特点是它能够在处理序列数据的同时在线地计算梯度。这意味着当网络处理每个时间步的数据时,它可以立即更新权重,而不需要等待整个序列被处理完毕。这种方法在理论上可以更好地适应动态环境,因为它可以在处理序列的过程中逐步优化模型。
优点:
- 能够实现真正的在线学习,适应实时数据流。
- 梯度计算与网络响应同时进行,提供灵活的计算框架。
缺点:
- 计算复杂度高,特别是在处理长序列时。
- 内存消耗大,需要存储雅可比矩阵。
RTRL算法原理:


上面, 表示Hadamard乘积(同或运算),即对应位置元素相乘。
(3)两种算法比较
RTFL算法和BPTT算法都是基于梯度下降的算法,分别通过前向模式和反向模式应用链式法则来计算梯度。
在循环神经网络中,一般网络输出维度远低于输入维度,因此BPTT算法的计算量会更小,但是BPTT算法需要保存所有时刻的中间梯度,空间复杂度较高。RTFL算法不需要梯度回传,因此非常适合用于需要在线学习或无限序列的任务中。
4. 基于门控的循环神经网络
为了改善循环神经网络的长程依赖问题,一种非常好的解决方案是引入门控机制来控制信息的累积速度,包括有选择地加入新的信息,并有选择地遗忘之前累积的信息。这一类网络可以称为基于门控的循环神经网络(Gated RNN)。
本文主要介绍两种基于门控的循环神经网络:长短期记忆网络和门控循环单元网络。
4.1 长短期记忆网络
长短期记忆网络(Long Short-Term Memory Network,LSTM)是循环神经网络的一个变体,可以有效地解决简单循环神经网络的梯度爆炸或消失问题。
第2.2节讲到,为了解决梯度消失问题,神经元可以采用以下策略:
LSTM网络是在上面公式的基础上,主要在以下两个方面进行了改进:
(1)新的内部状态
LSTM网络引入一个新的内部状态(internal state) 专门进行线性的循环信息传递,同时(非线性地)输出信息给隐藏层的外部状态
。内部状态
通过下面公式计算:

其中,遗忘门、输入门
、输出门
为三个门(gate)来控制信息传递的路径;
为向量元素乘积;
为上一时刻的记忆单元;
是通过非线性函数得到的候选状态:
![]()
在每个时刻 ,LSTM网络的内部状态
记录了到当前时刻为止的历史信息。
(2)门控机制
在数字电路中,门(gate)为一个二值变量 {0,1},0代表关闭状态,不许任何信息通过;1代表开放状态,允许所有信息通过。LSTM网络引入门控机制(Gating Mechanism)来控制信息传递的路径。三个门的作用为:
- 遗忘门:控制上一个时刻的内部状态
需要遗忘多少信息;
- 输入门:控制当前时刻的候选状态
有多少信息需要保存;
- 输出门:控制当前时刻的内部状态
有多少信息需要输出给外部状态
。
当 时,记忆单元将历史信息清空,并将候选状态向量
写入。但此时记忆单元
依然和上一时刻的历史信息相关。当
时,记忆单元将复制上一时刻的内容,不写入新的信息。
LSTM网络中的“门”是一种“软”门,取值在(0,1)之间,表示以一定的比例允许信息通过。三个门的计算方式为:

其中 为Logistic函数,其输出区间为(0,1),
为当前时刻的输入,
为上一时刻的外部状态。
下图给出了LSTM网络的循环单元结构,其计算过程为:
- 1)首先利用上一时刻的外部状态
和当前时刻的输入
,计算出三个门,以及候选状态
;
- 2)结合遗忘门
和输入门
来更新记忆单元
;
- 3)结合输出门
,将内部状态的信息传递给外部状态
。

通过 LSTM 循环单元,整个网络可以建立较长距离的时序依赖关系。
循环神经网络中的隐状态 存储了历史信息,可以看作一种记忆(Memory)。在简单循环网络中,隐状态每个时刻都会被重写,因此可以看作一种短期记忆(Short-Term Memory)。在神经网络中,长期记忆(Long-Term Memory)可以看作网络参数,隐含了从训练数据中学到的经验,其更新周期要远远慢于短期记忆。而在LSTM网络中,记忆单元
可以在某个时刻捕捉到某个关键信息,并有能力将此关键信息保存一定的时间间隔。记亿单元
中保存信息的生命周期要长于短期记忆,但又远远短于长期记忆,因此称为长短期记忆(LongShort-Term Memory)。

4.2 LSTM网络的变体网络


4.3 门控循环单元网络
门控循环单元(Gated Recurrent Unit,GRU)网络是一种比LSTM网络更加简单的循环神经网络。
GRU网络引入门控机制来控制信息更新的方式。和LSTM不同,GRU不引入额外的记亿单元,GRU网络是引入一个更新门(Update Gate)来控制当前状态需要从历史状态中保留多少信息,以及需要从候选状态中接受多少新信息,即:
其中, 为更新门:
在LSTM网络中,输入门和遗忘门是互补关系,具有一定的冗余性,而GRU网络直接使用一个门来控制输入和遗忘之间的平衡。下图为GRU网络的循环单元结构:

5. 深层循环神经网络
增加循环神经网络的深度可以增强循环神经网络的能力,这里的增加深度主要是增加同一时刻网络输入到输出之间的路径 →
,比如增加隐状态到输出
→
,以及输入到隐状态
→
之间的路径的深度。
5.1 堆叠循环神经网络
一种常见的增加循环神经网络深度的做法是将多个循环网络堆叠起来,称为堆叠循环神经网络(Stacked Recurrent Neural Network,SRNN)。一个堆叠的简单循环网络(Stacked SRN)也称为循环多层感知器(Recurrent Multi-Layer Perceptron,RMLP)。
下图给出了按时间展开的堆叠循环神经网络:

第 层网络的输入是第
层网络的输出。定义
为在时刻
时第
层的隐状态:
其中,、
和
为权重矩阵和偏置向量,
。
5.2 双向循环神经网络
在有些任务中,一个时刻的输出不但和过去时刻的信息有关,也和后续时刻的信息有关。比如给定一个句子,其中一个词的词性由它的上下文决定,即包含左右两边的信息。因此,在这些任务中,我们可以增加一个按照时间的逆序来传递信息的网络层,来增强网络的能力。
双向循环神经网络(Bidirectional Recurrent Neural Network,Bi-RNN)由两层循环神经网络组成,它们的输入相同,只是信息传递的方向不同。
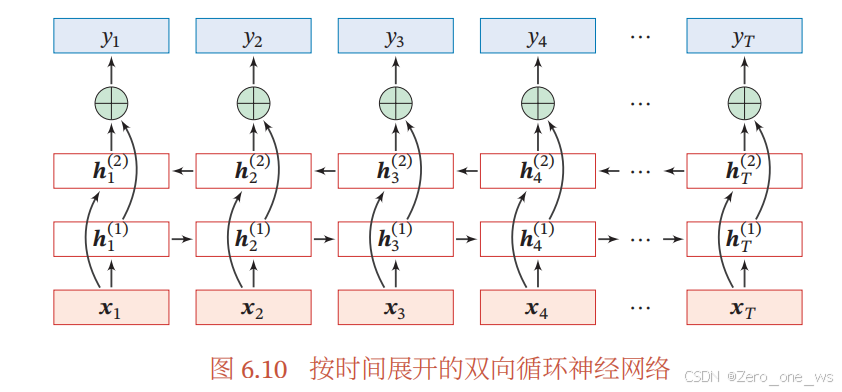
假设第1层按时间顺序,第2层按时间逆序,在时刻 时的隐状态定义为
和
,则:

其中, 为向量拼接操作。
下图为按时间展开的双向循环神经网络:






















 728
728

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








