贝叶斯优化基础方法

---

前言

目前机器学习领域中常见的超参数优化方法包括网格搜索、随机网格搜索、Halving网格搜索与贝叶斯优化。
其中网格搜索、随机网格搜索与Halving网格搜索，无论具体每种网格搜索的思想如何变化，网格优化都是在一个大参数空间中、尽量对所有点进行验证后再返回最优损失函数值的方法，这一类方法在计算量与计算时间上有着不可避免的缺陷，因此才会有随机、Halving等试图缩短训练时间、让整体网格搜索更加适合于大型数据和大型空间的手段。然而，尽管sklearn在提高网格搜索效率方面做出了种种优化，但上述方法仍然无法在效率和精度上做到双赢，若希望更快速的进行参数搜索、并且搜索出一组泛化能力尽可能强的参数，目前的常见做法还是选用一些带有先验过程的调参工具，即一些基于贝叶斯过程调参工具。

---

一、贝叶斯优化是什么？

贝叶斯优化方法是当前超参数优化领域的SOTA手段（State of the Art），可以被认为是当前最为先进的优化框架，它可以被应用于AutoML的各大领域，不止限于超参数搜索HPO的领域，更是可以被用于神经网络架构搜索NAS以及元学习等先进的领域。现代几乎所有在效率和效果上取得优异成果的超参数优化方法都是基于贝叶斯优化的基本理念而形成的，因此贝叶斯优化是整个AutoML中学习的重点。

二、贝叶斯优化基本流程

首先，我们不理会HPO的问题，先来看待下面的例子。假设现在我们知道一个函数$f(x)$的表达式以及其自变量$x$的定义域，现在，我们希望求解出$x$的取值范围上$f(x)$的最小值，你打算如何求解这个最小值呢？面对这个问题，无论是从单纯的数学理论角度，还是从机器学习的角度，我们都已经见过好几个通俗的思路：

• 1 我们可以对$f(x)$求导、令其一阶导数为0来求解其最小值

函数$f(x)$可微，且微分方程可以直接被求解

• 2 我们可以通过梯度下降等优化方法迭代出$f(x)$的最小值

函数$f(x)$可微，且函数本身为凸函数

• 3 我们将全域的$x$带入$f(x)$计算出所有可能的结果，再找出最小值

函数$f(x)$相对不复杂、自变量维度相对低、计算量可以承受

当我们知道函数$f(x)$的表达式时，以上方法常常能够有效，但每个方法都有自己的前提条件。假设现在函数$f(x)$是一个平滑均匀的函数，但它异常复杂、且不可微，我们无法使用上述三种方法中的任意一种方法求解，但我们还是想求解其最小值，可以怎么办呢？由于函数异常复杂，带入任意$x$计算的所需的时间很长，所以我们不太可能将全域$x$都带入进行计算，但我们还是可以从中随机抽样部分观测点来观察整个函数可能存在的趋势。于是我们选择在$x$的定义域上随机选择了4个点，并将4个点带入$f(x)$进行计算，得到了如下结果：

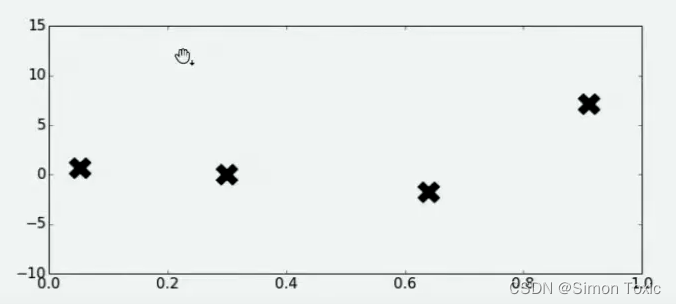
好了，现在有了这4个观测值，你能告诉我$f(x)$的最小值在哪里吗？你认为最小值点可能在哪里呢？大部分人会倾向于认为，最小值点可能非常接近于已观测出4个$f(x)$值中最小的那个值，但也有许多人不这么认为。当我们有了4个观测值，并且知道我们的函数时相对均匀、平滑的函数，那我们可能对函数的整体分布有如下猜测：

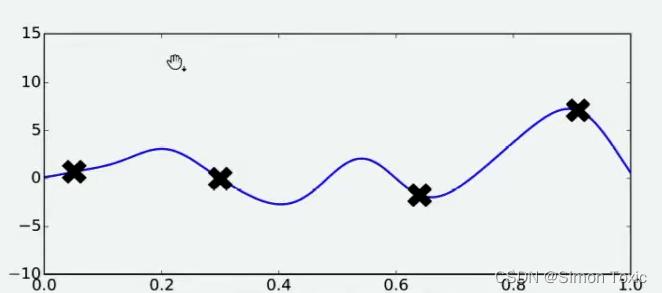
当我们对函数整体分布有一个猜测时，这个分布上一定会存在该函数的最小值。同时，不同的人可能对函数的整体分布有不同的猜测，不同猜测下对应的最小值也是不同的。

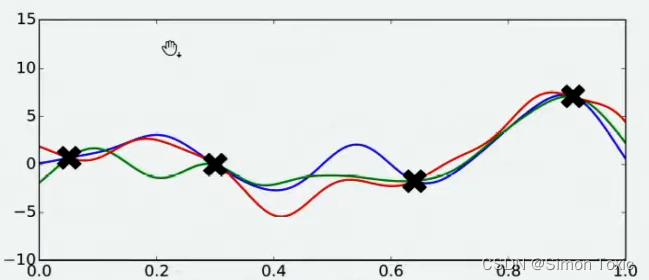
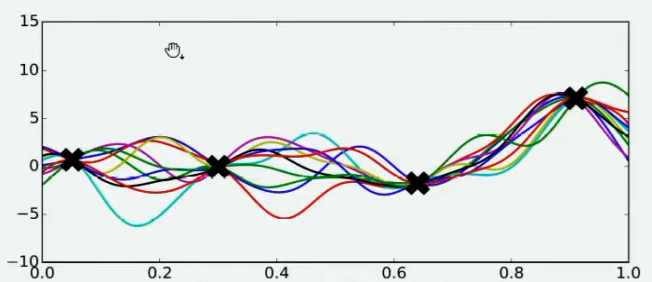
现在假设我们邀请了数万个人对该问题做出猜测，每个人所猜测的曲线如下图所示。不难发现，在观测点的附近，每个人猜测的函数值差距不大，但是在远离远侧点的地方，每个人猜测的函数值就高度不一致了。这也是当然的，因为观测点之间函数的分布如何完全是未知的，并且该分布离观测点越远时，我们越不确定真正的函数值在哪里，因此人们猜测的函数值的范围非常巨大。

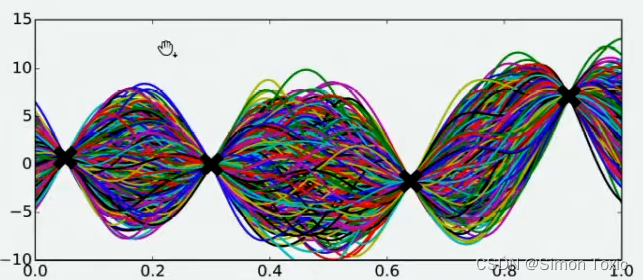
现在，我们将所有猜测求均值，并将任意均值周围的潜在函数值所在的区域用色块表示，可以得到一条所有人猜测的平均曲线。不难发现，色块所覆盖的范围其实就是大家猜测的函数值的上界和下界，而任意$x$所对应的上下界差异越大，表示人们对函数上该位置的猜测值的越不确定。因此上下界差异可以衡量人们对该观测点的置信度，色块范围越大，置信度越低。

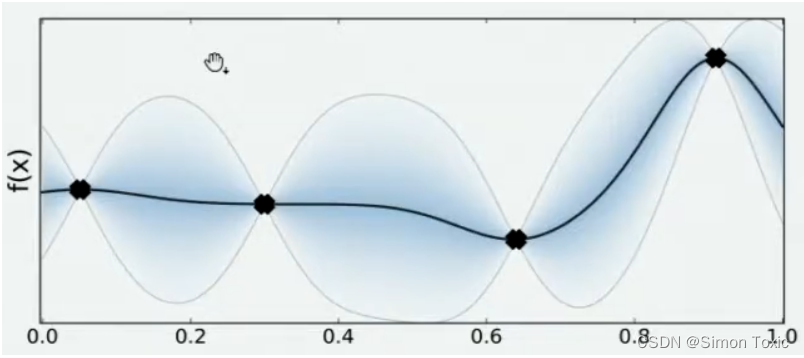
在观测点周围，置信度总是很高的，远离观测点的地方，置信度总是很低，所以如果我们能够在置信度很低的地方补充一个实际的观测点，我们就可以很快将众人的猜测统一起来。以下图为例，当我们在置信度很低的区间内取一个实际观测值时，围绕该区间的“猜测”会立刻变得集中，该区间内的置信度会大幅升高。

当整个函数上的置信度都非常高时，我们可以说我们得出了一条与真实的$f(x)$曲线高度相似的曲线$f^{\ast }$，次数我们就可以将$f^{\ast }$的最小值当作真实$f(x)$的最小值来看待。自然，如果估计越准确，$f^{\ast }$越接近$f(x)$，则$f^{\ast }$的最小值也会越接近于$f(x)$的真实最小值。那如何才能够让$f^{\ast }$更接近$f(x)$呢？根据我们刚才提升置信度的过程，很明显——观测点越多，我们估计出的曲线会越接近真实的$f(x)$。然而，由于计算量有限，我们每次进行观测时都要非常谨慎地选择观测点。那现在，如何选择观测点才能够最大程度地帮助我们估计出$f(x)$的最小值呢？

有非常多的方法，其中最简单的手段是使用最小值出现的频数进行判断。由于不同的人对函数的整体分布有不同的猜测，不同猜测下对应的最小值也是不同的，根据每个人猜测的函数结果，我们在$X$轴上将定义域区间均匀划分为100个小区间，如果有某个猜测的最小值落在其中一个区间中，我们就对该区间进行计数（这个过程跟对离散型变量绘制直方图的过程完全一致）。当有数万个人进行猜测之后，我们同时也绘制了基于$X$轴上不同区间的频数图，频数越高，说明猜测最小值在该区间内的人越多，反之则说明该猜测最小值在该区间内的人越少。该频数一定程度上反馈出最小值出现的概率，频数越高的区间，函数真正的最小值出现的概率越高。

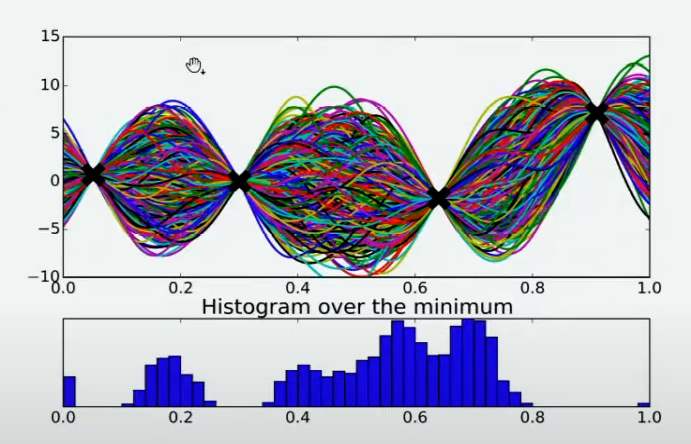
当我们将$X$轴上的区间划分得足够细后，绘制出的频数图可以变成概率密度曲线，曲线的最大值所对应的点是$f(x)$的最小值的概率最高，因此很明显，我们应该将曲线最大值所对应的点确认为下一个观测点。根据图像，我们知道最小值最有可能在的区间就在x=0.7左右的位置。当我们不取新的观测点时，现在$f(x)$上可以获得的可靠的最小值就是x=0.6时的点，但我们如果在x=0.7处取新的观测值，我们就很有可能找到比当前x=0.6的点还要小的$f_{min}$。因此，我们可以就此决定，在x=0.7处进行观测。
在观测点周围，置信度总是很高的，远离观测点的地方，置信度总是很低，所以如果我们能够在置信度很低的地方补充一个实际的观测点，我们就可以很快将众人的猜测统一起来。以下图为例，当我们在置信度很低的区间内取一个实际观测值时，围绕该区间的“猜测”会立刻变得集中，该区间内的置信度会大幅升高。

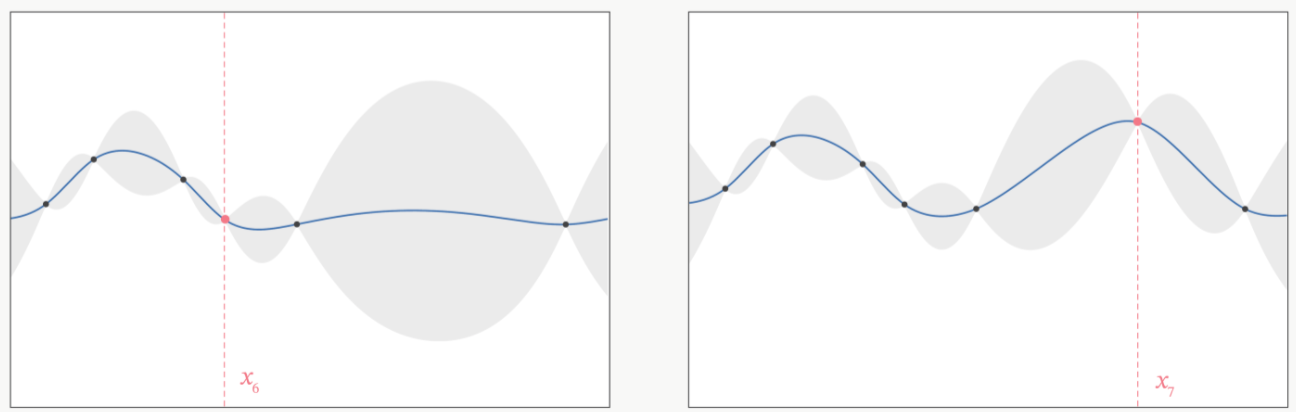
当整个函数上的置信度都非常高时，我们可以说我们得出了一条与真实的$f(x)$曲线高度相似的曲线$f^{\ast }$，次数我们就可以将$f^{\ast }$的最小值当作真实$f(x)$的最小值来看待。自然，如果估计越准确，$f^{\ast }$越接近$f(x)$，则$f^{\ast }$的最小值也会越接近于$f(x)$的真实最小值。那如何才能够让$f^{\ast }$更接近$f(x)$呢？根据我们刚才提升置信度的过程，很明显——观测点越多，我们估计出的曲线会越接近真实的$f(x)$。然而，由于计算量有限，我们每次进行观测时都要非常谨慎地选择观测点。那现在，如何选择观测点才能够最大程度地帮助我们估计出$f(x)$的最小值呢？

有非常多的方法，其中最简单的手段是使用最小值出现的频数进行判断。由于不同的人对函数的整体分布有不同的猜测，不同猜测下对应的最小值也是不同的，根据每个人猜测的函数结果，我们在$X$轴上将定义域区间均匀划分为100个小区间，如果有某个猜测的最小值落在其中一个区间中，我们就对该区间进行计数（这个过程跟对离散型变量绘制直方图的过程完全一致）。当有数万个人进行猜测之后，我们同时也绘制了基于$X$轴上不同区间的频数图，频数越高，说明猜测最小值在该区间内的人越多，反之则说明该猜测最小值在该区间内的人越少。该频数一定程度上反馈出最小值出现的概率，频数越高的区间，函数真正的最小值出现的概率越高。

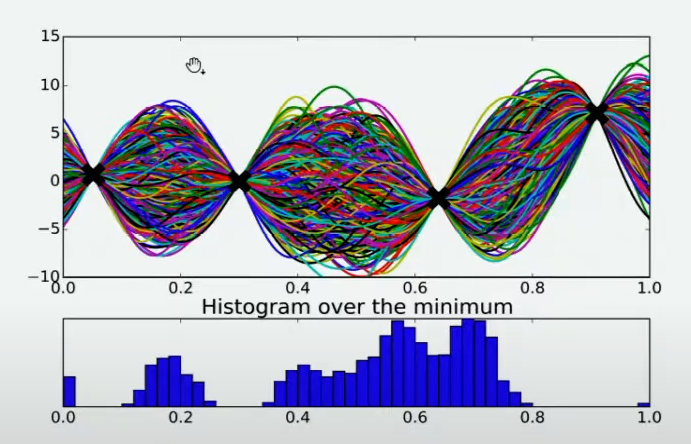
当我们将$X$轴上的区间划分得足够细后，绘制出的频数图可以变成概率密度曲线，曲线的最大值所对应的点是$f(x)$的最小值的概率最高，因此很明显，我们应该将曲线最大值所对应的点确认为下一个观测点。根据图像，我们知道最小值最有可能在的区间就在x=0.7左右的位置。当我们不取新的观测点时，现在$f(x)$上可以获得的可靠的最小值就是x=0.6时的点，但我们如果在x=0.7处取新的观测值，我们就很有可能找到比当前x=0.6的点还要小的$f_{min}$。因此，我们可以就此决定，在x=0.7处进行观测。

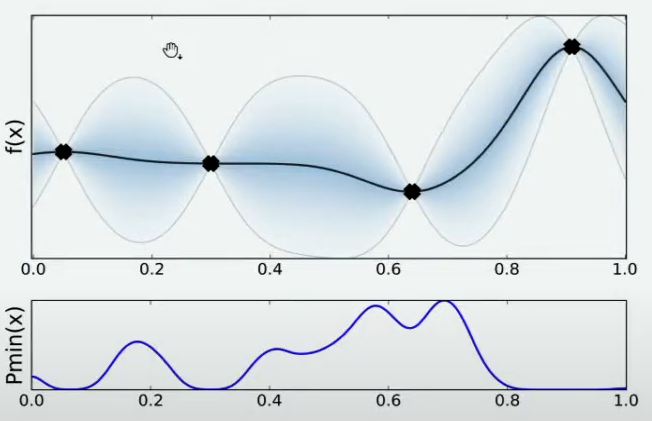
当我们在x=0.7处取出观测值之后，我们就有了5个已知的观测点。现在，我们再让数万人根据5个已知的观测点对整体函数分布进行猜测，猜测完毕之后再计算当前最小值频数最高的区间，然后再取新的观测点对$f(x)$进行计算。当允许的计算次数被用完之后（比如，500次），整个估计也就停止了。
你发现了吗？在这个过程当中，我们其实在不断地优化我们对目标函数$f(x)$的估计，虽然没有对$f(x)$进行全部定义域上的计算，也没有找到最终确定一定是$f(x)$分布的曲线，但是随着我们观测的点越来越多，我们对函数的估计是越来越准确的，因此也有越来越大的可能性可以估计出$f(x)$真正的最小值。这个优化的过程，就是贝叶斯优化。

二、贝叶斯优化用于HPO

---

在贝叶斯优化的数学过程当中，我们主要执行以下几个步骤：

• 1 定义需要估计的$f(x)$以及$x$的定义域
  

• 2 取出有限的n个$x$上的值，求解出这些$x$对应的$f(x)$（求解观测值）
  

• 3 根据有限的观测值，对函数进行估计（该假设被称为贝叶斯优化中的先验知识），得出该估计$f^{\ast }$上的目标值（最大值或最小值）
  

• 4 定义某种规则，以确定下一个需要计算的观测点

并持续在2-4步骤中进行循环，直到假设分布上的目标值达到我们的标准，或者所有计算资源被用完为止（例如，最多观测m次，或最多允许运行t分钟）。

---

以上流程又被称为序贯模型优化（SMBO），是最为经典的贝叶斯优化方法。在实际的运算过程当中，尤其是超参数优化的过程当中，有以下具体细节需要注意：

• 当贝叶斯优化不被用于HPO时，一般$f(x)$可以是完全的黑盒函数（black box function，也译作黑箱函数，即只知道$x$与$f(x)$的对应关系，却丝毫不知道函数内部规律、同时也不能写出具体表达式的一类函数），因此贝叶斯优化也被认为是可以作用于黑盒函数估计的一类经典方法。但在HPO过程当中，需要定义的$f(x)$一般是交叉验证的结果/损失函数的结果，而我们往往非常清楚损失函数的表达式，只是我们不了解损失函数内部的具体规律，因此HPO中的$f(x)$不能算是严格意义上的黑盒函数。

• 在HPO中，自变量$x$就是超参数空间。在上述二维图像表示中，$x$为一维的，但在实际进行优化时，超参数空间往往是高维且极度复杂的空间。

• 最初的观测值数量n、以及最终可以取到的最大观测数量m都是贝叶斯优化的超参数，最大观测数量m也决定了整个贝叶斯优化的迭代次数。

• 在第3步中，根据有限的观测值、对函数分布进行估计的工具被称为概率代理模型（Probability Surrogate model），毕竟在数学计算中我们并不能真的邀请数万人对我们的观测点进行连线。这些概率代理模型自带某些假设，他们可以根据廖廖数个观测点估计出目标函数的分布$f^{\ast }$（包括$f^{\ast }$上每个点的取值以及该点对应的置信度）。在实际使用时，概率代理模型往往是一些强大的算法，最常见的比如高斯过程、高斯混合模型等等。传统数学推导中往往使用高斯过程，但现在最普及的优化库中基本都默认使用基于高斯混合模型的TPE过程。

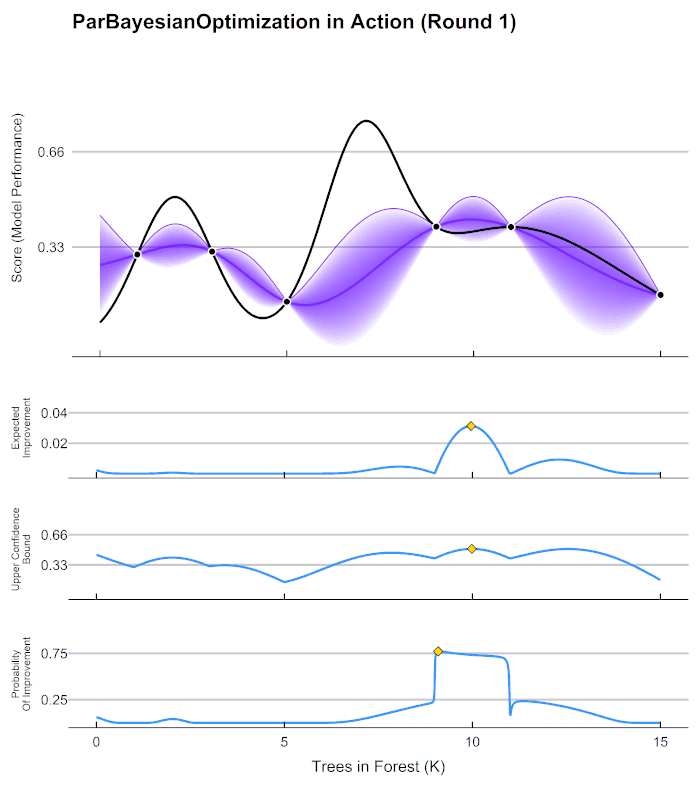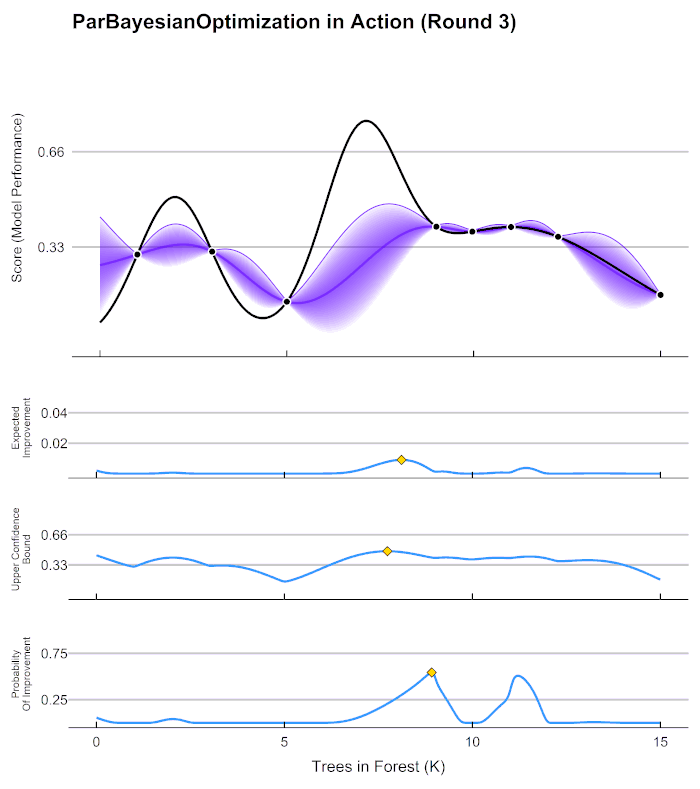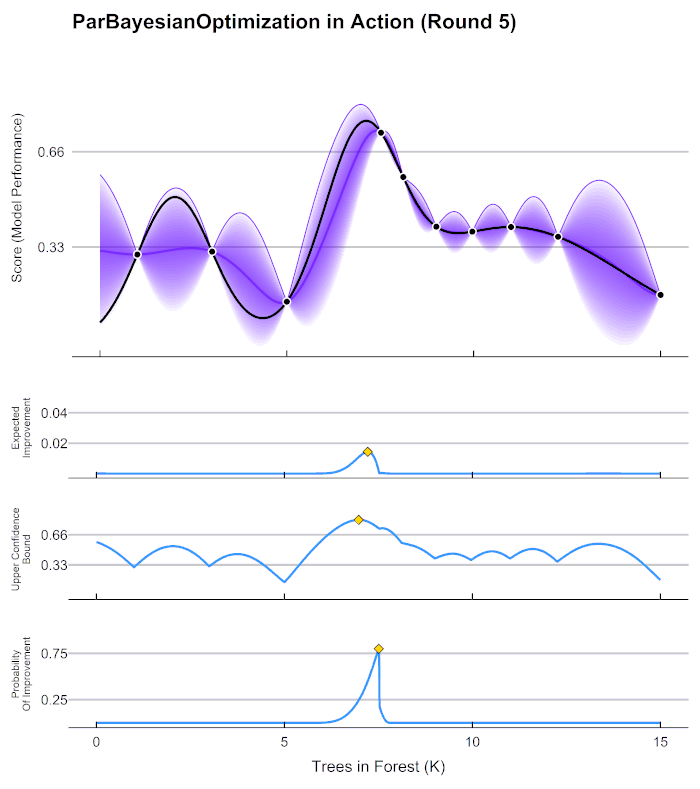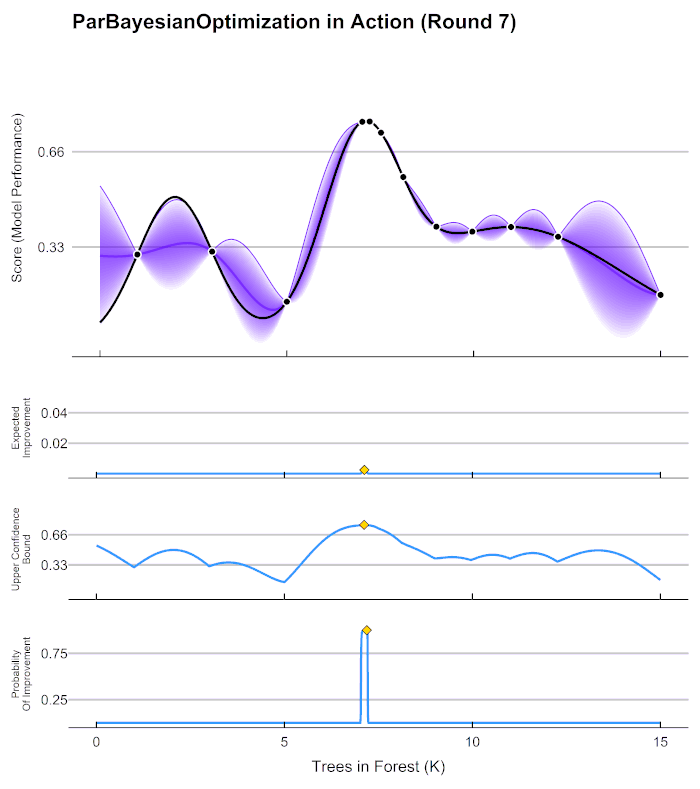
• 在第4步中用来确定下一个观测点的规则被称为采集函数（Aquisition Function），采集函数衡量观测点对拟合$f^{\ast }$所产生的影响，并选取影响最大的点执行下一步观测，因此我们往往关注采集函数值最大的点。最常见的采集函数主要是概率增量PI（Probability of improvement，比如我们计算的频数）、期望增量（Expectation Improvement）、置信度上界（Upper Confidence Bound）、信息熵（Entropy）等等。上方gif图像当中展示了PI、UCB以及EI。其中大部分优化库中默认使用期望增量。

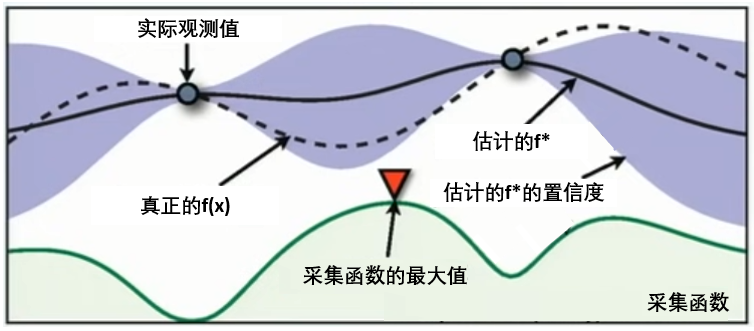
在HPO中使用贝叶斯优化时，我们常常会看见下面的图像，这张图像表现了贝叶斯优化的全部基本元素，我们的目标就是在采集函数指导下，让$f^{\ast }$尽量接近$f(x)$。

总结

以上就是对贝叶斯优化的基本流程的介绍。在下一篇中将会介绍如何应用贝叶斯优化的各类库实现不同的贝叶斯优化算法。