Smart “Predict, then Optimize”

摘要

许多现实世界的分析问题涉及两个重大挑战：预测和优化。 由于每个挑战的典型复杂性，标准范式是预测然后优化。 总的来说，机器学习工具旨在最大限度地减少预测误差，并没有考虑在下游优化问题中将如何使用预测。 相比之下，我们提出了一个新的非常通用的框架，称为智能“预测，然后优化”（SPO），它直接利用优化问题的结构，即它的目标和约束，来设计更好的预测模型。 我们框架的一个关键组成部分是 SPO 损失函数，它测量由预测引起的决策误差。
训练关于 SPO 损失的预测模型在计算上具有挑战性，因此我们使用对偶理论推导出一个凸替代损失函数，我们称之为 SPO+损失。 最重要的是，我们证明了 SPO+ 损失与温和条件下的 SPO 损失在统计上是一致的。
我们的 SPO+ 损失函数可以轻松处理任何具有线性目标的多面体、凸面甚至混合整数优化问题。 最短路径和投资组合优化问题的数值实验表明，SPO 框架可以在预测然后优化范式下带来显着的改进，特别是当正在训练的预测模型被错误指定时。 我们发现使用 SPO+ 损失训练的线性模型往往会主导随机森林算法，即使基本事实是高度非线性的。
关键词：规范分析； 数据驱动的优化； 机器学习； 线性回归

引言

在运筹学的许多实际分析应用中，机器学习和优化的组合被用来做出决策。 通常，优化模型用于生成决策，而机器学习工具用于生成预测模型，该模型预测优化模型的关键未知参数。 由于这两项任务固有的复杂性，分析实践中经常采用的广泛用途方法是预测然后优化范式。
例如，考虑一天可能要解决多次的车辆路径问题。
首先，预先训练的预测模型根据当前交通、天气、假期、时间等，对道路网络所有边缘的行程时间进行预测。
优化求解器使用预测的旅行时间作为输入提供接近最优的路线。
我们强调，现实世界分析问题的大多数解决方案系统都涉及预测和优化的某些组成部分（参见 Angalakudati 等人（2014 年）、Chan 等人。
(2012), Deo 等人。 （2015 年），加利恩等人。 (2015)，科恩等人。 (2017), Besbes 等人。 (2015), Mehrotra 等人。 (2011)，陈等人。 （2013 年），费雷拉等人。 （2015 年）Simchi-Levi（2013 年）、den Hertog 和 Postek（2016 年）、Deng 等人最近的例子和最近的论述。 (2018)、Mišić 和 Perakis (2020))。 除了一些有限的选项外，机器学习工具并没有有效地说明预测将如何用于下游优化问题。 在本文中，我们提供了一个称为智能“预测，然后优化”（SPO）的通用框架，用于训练有效利用名义优化问题结构（即其约束和目标）的预测模型。 我们的 SPO 框架从根本上设计为生成旨在最小化决策错误而非预测错误的预测模型。
我们的 SPO 方法的一个主要好处是它保持了顺序预测然后优化的决策范式。 然而，在训练我们的预测模型时，显式使用了名义优化问题的结构。 预测的质量不是基于预测误差（例如最小二乘损失或其他流行的损失函数）来衡量的。 相反，在 SPO 框架中，预测的质量由决策误差来衡量。 也就是说，假设使用历史特征数据（x1，…，xn）和相关参数数据（c1，…，cn）训练预测模型。 让 (ˆc1, . . ., cˆn) 表示训练模型下参数的预测。 例如，最小二乘 (LS) 损失用平方范数 kci − cˆik 2 2 测量误差，完全忽略由预测引起的决策。 相比之下，SPO 损失是由 c^i 引起的决策的真实成本减去真实参数 ci 下的最优成本。 在车辆路线规划的背景下，SPO 损失衡量由于在预测的而不是真实的边缘成本参数上解决路线问题而导致的额外旅行时间。
在本文中，我们专注于预测上下文随机优化问题的未知参数，其中参数在目标函数中线性出现，即任何线性、凸或整数优化问题的成本向量。 我们的 SPO 框架的核心是用于训练预测模型的新损失函数。 由于 SPO 损失函数难以使用，因此大量工作围绕着导出替代损失函数 SPO+ 展开，该函数是凸的，因此可以有效地优化。 为了证明有效性替代 SPO+ 损失，我们证明了非常理想的统计一致性属性，并表明与标准的预测然后优化方法相比，它在经验上表现良好。
本质上，我们证明了最小化与 SPO+损失相关的贝叶斯风险的函数是回归函数 E[c|x]，它也最小化了 SPO 损失的贝叶斯风险（在温和的假设下）。 有趣的是，在相同条件下，E[c|x] 还最小化了与 LS 损失相关的贝叶斯风险。 因此，SPO+ 和 LS（或两者的任何凸组合）本质上是“平等​​的”——对于损失函数，它们在理论上都是有效的（一致的）和计算上易于处理的选择。 然而，当最终目标是解决下游优化任务时，SPO+ 损失是自然的选择，因为它是为优化问题量身定制的，并且在实践中比 LS 好得多。
根据经验，我们观察到，即使由于模型指定错误而导致预测任务具有挑战性，SPO 框架仍然可以产生接近最优的决策。 我们注意到 SPO 框架的一个基本属性是要求将预测直接“插入”到下游优化问题中。 替代程序可能会以某种方式改变决策过程，例如通过增加稳健性或通过考虑整个数据集（而不仅仅是预测）。 我们的 SPO 方法的一个强大优势是，即使在朴素的预测问题具有挑战性时，它也具有良好的性能，请参见第 3.1 节中的说明性示例。 另一个优点是下游优化问题通常比更复杂的替代程序在计算上更易于处理并且对从业者更具吸引力。 另一方面，替代决策程序可以提供其他优势，例如通过引入偏差和/或鲁棒性提高泛化性能。 然而，在存在上下文数据的情况下设计此类程序更具挑战性，将它们与 SPO 方法相结合将是值得未来研究的。 总的来说，我们相信我们的 SPO 框架为设计可在现实世界优化设置中使用的操作驱动的机器学习工具提供了清晰的基础。
我们的贡献可以总结如下： 1. 我们首先正式定义了一个新的损失函数，我们称之为 SPO 损失，它测量预测具有线性、凸或整数约束的名义优化问题的成本向量时的误差。 损失对应于次优差距 - 相对于真实/历史成本向量 - 由于实施了由预测成本向量引起的可能不正确的决策。 不幸的是，SPO 损失函数可能是非凸的，并且预测不连续，这意味着在 SPO 损失下训练 ML 模型可能具有挑战性。
2. 鉴于 SPO 损失函数的难处理性，我们开发了一个替代损失函数，我们称之为 SPO+ 损失。 该替代损失函数是使用由对偶理论（命题 2）、数据缩放近似和一阶近似激发的一系列步骤推导出来的。 由此产生的 SPO+ 损失函数在预测中是凸的（命题 3），这使我们能够设计一种基于随机梯度下降的算法，以最小化 SPO+ 损失（命题 8）。 而且，在训练线性回归模型来预测线性程序的客观系数时，只需要解决一个线性优化问题即可最小化 SPO+损失（命题 7）。
3. 我们在 SPO 框架的一个非常简单和特殊的实例下证明了与经典机器学习的基本联系。 也就是说，在这种情况下，SPO 损失恰好是 0-1 分类损失（命题 1），而 SPO+ 损失恰好是铰链损失（命题 4）。 铰链损失是流行的 SVM 方法的基础，是近似最小化 0-1 损失的替代损失，因此我们的框架将这个概念推广到一个非常广泛的具有约束的优化问题系列。
4. 我们证明了 SPO+ 损失函数的关键一致性结果（定理 1、命题 5、命题 6），这进一步激发了它的使用。 也就是说，在完整的分布知识下，如果两个温和的条件成立，最小化 SPO+ 损失函数实际上等效于最小化 SPO 损失：成本向量的分布（给定特征）是连续的并且关于其均值对称。 例如，标准高斯噪声近似满足这些假设。 这种一致性属性被广泛认为是统计和机器学习文献中任何替代损失函数的基本属性。 比如著名的hinge loss和logistic loss函数就符合0-1分类损失。
5. 最后，我们通过最短路径和投资组合优化问题的数值实验来验证我们的框架。 我们根据标准的预测然后优化方法测试我们的 SPO 框架，并评估与 SPO 损失相关的样本外性能。 一般来说，我们的 SPO 框架的价值随着模型错误指定程度的增加而增加。 这正是因为 SPO 框架做出了“更好”的错误预测，本质上是“欺骗”优化问题以寻找接近最优的解决方案。 值得注意的是，使用 SPO+ 训练的线性模型甚至在最先进的随机森林算法中占主导地位，即使基本事实是高度非线性的。
1.1应用
需要从上下文（特征）数据预测优化问题的输入参数（成本向量）的设置很多。 现在让我们重点介绍 SPO 框架的一些应用领域，其中可能有很多。
车辆路线。 在许多应用中，需要在做出路由决策之前预测图每条边的成本。 边的成本通常对应于车辆穿越相应边所需的预期时间长度。 为了清楚起见，让我们关注一个重要的例子——最短路径问题。 在最短路径问题中，给定一个带权有向图，以及一个起点节点和终点节点，目标是以最小的成本找到从起点到终点的一系列边。 一个众所周知的事实是，最短路径问题可以表述为线性优化问题，但也有替代的专门算法，例如著名的 Dijkstra 算法（参见，例如，Ahuja 等人（1993））。 用于预测边缘成本的数据可能包括长度、速度限制、天气、季节、日期以及来自谷歌地图和 Waze 等移动应用程序的实时数据。 简单地最小化预测误差可能不够也不合适，因为高估或低估对整个网络的影响截然不同。 SPO 框架将确保预测的权重导致最短路径，并且自然会强调对这一决策至关重要的边估计。 有关深入示例，请参见第 2 节中的图 3
Inventory Management. 在库存计划问题中，例如经济批量大小问题（Wagner 和 Whitin（1958））或联合补货问题（Levi et al.
(2006))，需求是优化模型的关键输入。 在实际环境中，需求是高度不稳定的，可能取决于历史和上下文数据，例如天气、季节性和竞争对手的销售额。 何时订购库存的决定由线性或整数优化模型捕获，具体取决于问题的复杂性。 在一个常见的公式下（见 Levi et al. (2006), Cheung et al. (2016)），需求在目标中线性出现，这对于 SPO 框架来说很方便。 目标是设计一个预测模型，将特征数据映射到需求预测，进而产生良好的库存计划。
投资组合优化。 在金融服务应用中，潜在投资的回报需要以某种方式从数据中估计出来，并且可能取决于许多特征，通常包括历史回报、新闻、经济因素、社交媒体等。 在
typically include historical returns, news, economic factors, social media, and others. In 投资组合优化，目标是在投资组合的总风险或方差的约束下找到具有最高回报的投资组合。 虽然回报通常高度依赖于辅助特征信息，但方差通常要稳定得多，而且预测起来并不困难也不敏感。 我们的 SPO 框架将导致预测，从而导致满足所需风险水平的高性能投资。 最小二乘损失方法更加强调估计更高价值的投资，即使相应的风险可能并不理想。 相比之下，SPO 框架在训练预测模型时直接考虑了每项投资的风险。
1.2相关工作
也许最相关的工作是 Kao 等人的工作。 (2009)，他还直接寻求训练一个机器学习模型，该模型可以最大限度地减少名义优化问题的损失。 在他们的框架中，名义问题是一个无约束的二次优化问题，其中未知参数出现在目标的线性部分。 他们的工作并没有扩展到名义优化问题有约束的设置，而我们的框架会这样做。 唐蒂等人。 (2017) 提出了一种启发式方法来解决比 Kao 等人更一般的设置。 (2009)，并且还关注二次优化的情况。
这些工作还绕过了名义问题解的非唯一性问题（因为它们的问题是强凸的），必须在我们的设置中解决这些问题以避免退化的预测模型。
在 Ban 和 Rudin (2019) 中，训练 ML 模型以直接从数据预测报摊问题的最佳解决方案。 显示了该方法的可处理性和统计特性以及它在实践中的有效性。 但是，在存在限制的情况下如何使用这种方法尚不清楚，因为可能会出现可行性问题
Bertsimas 和 Kallus (2020) 中的一般方法考虑了使用机器学习模型准确估计未知优化目标的问题，特别是 ML 模型，其中预测可以描述为训练样本的加权组合，例如最近邻和决策树。 在他们的方法中，他们通过将 ML 模型生成的相同权重应用于这些样本的相应目标函数来估计实例的目标。 只有当目标函数在未知参数中为非线性时，这种方法才不同于标准的先预测后优化。 请注意，1.1 节中提到的所有应用程序的未知参数
线性地出现在物镜中。 此外，与 SPO 框架相比，ML 模型的训练不依赖于名义优化问题的结构。
Tulabandhula 和 Rudin (2013) 中的方法依赖于最小化损失函数，该函数将预测误差与模型在未标记数据集上的操作成本相结合。
但是，运营成本与预测参数有关，而不是与真实参数有关。 Gupta 和 Rusmevichientong (2017) 考虑在没有特征/上下文的设置中结合估计和优化。 我们还注意到，我们的 SPO 损失虽然在数学上不同，但在精神上与 Lim 等人中引入的相对遗憾的概念相似。 (2012) 在具有历史回报数据和没有特征的投资组合优化的特定背景下。 从数据中寻找接近最优解的其他方法包括操作统计（Liyanage 和 Shanthikumar（2005）、Chu 等（2008））、样本平均近似（Kleywegt 等（2002）、Schütz 等（2009）， Bertsimas 等人 (2018b)) 和稳健优化（Bertsimas 和 Thiele（2006 年）、Bertsimas 等人（2018a）、Wang 等人）。
(2016))。 最近在样本的子模块优化方面也取得了一些进展（Balkanski et al. (2016, 2017)）。 这些方法通常没有明确的使用特征数据的方式，也没有直接考虑如何训练机器学习模型来预测优化参数。
另一个相关的工作流是数据驱动的逆向优化，其中观察到优化问题的可行或最佳解决方案，并且必须学习目标函数（Aswani 等人（2018）、Keshavarz 等人（2011）、Chan 等人（2014 年）、Bertsimas 等人（2015 年）、Esfahani 等人（2018 年）。 在这些问题中，通常有一个未知的目标，并且没有提供目标的先前样本。 我们还注意到，最近有一些正则化方法（Ban 等人（2018 年））和模型选择（Besbes 等人（2010 年）、Den Boer 和 Sierag（2016 年）、Sen 和 Deng（2017 年））在 一个优化问题。
最后，我们注意到我们的框架与结构化预测的一般设置有关（参见，例如 Taskar 等人（2005）、Tsochantaridis 等人（2005）、Nowozin 等人（2011）、Osokin 等人（ 2017）和其中的参考资料）。 受计算机视觉和自然语言处理问题的启发，结构化预测是多类分类的一种版本，它涉及从特征数据中预测结构化对象，例如序列或图形。 SPO+ 损失在本质上与结构化 SVM (SSVM) 相似，并且确实是 SPO 损失的凸上界，类似于 SSVM。 然而，有与我们的方法和 SSVM 方法有根本区别。 在 SSVM 方法中，要预测的结构化对象是直接从特征 x 中得到的决策 w（Taskar et al. (2005)）。 在我们的设置中，我们可以访问关于 c 的历史数据，这比对决策的观察更丰富，因为成本向量自然会导致最优决策。
在我们框架的一种特殊情况下，我们证明 SPO 损失相当于 0/1 损失，而 SPO+ 损失相当于铰链损失。 因此，我们的框架可以看作是 SSVM 的一种泛化。 最后，我们注意到，我们对替代 SPO+ 损失的推导依赖于使用对偶理论的全新想法，这有助于解释强大的经验表现。

预测再优化框架

我们现在描述“预测，然后优化”框架，它是实践中许多优化应用的核心。 具体来说，我们假设存在一个具有线性目标的标称优化问题，其中决策变量 w ∈ R d 和可行区域 S ⊆ R d 是明确定义的并且是确定性的。 但是，目标的成本向量 c ∈ R d 在必须做出决定时不可用； 相反，一个相关的特征向量 x ∈ R p 是可用的。 设 Dx 是给定 x 的 c 的条件分布。
决策者的目标是解决任何以 x 为特征的新实例的上下文随机优化问题

预测然后优化框架依赖于使用对 Ec∼Dx [c|x] 的预测，我们用 cˆ 表示，并基于 cˆ 解决优化问题的确定性版本，即 minw∈S cˆ ⊤w。 我们在本文中的主要兴趣在于为预测然后优化框架定义合适的损失函数，检查它们的属性，以及开发使用这些损失函数训练预测模型的算法。
我们现在正式列出我们框架的关键成分：
1.名义（下游）优化问题，其形式为

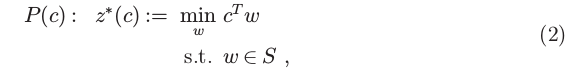
其中 w ∈ R d 是决策变量， c ∈ R d 是描述线性目标函数的问题数据， S ⊆ R d 是一个非空的、紧凑的（即，封闭和有界），并且
表示可行区域的凸集。由于我们这里关注的是线性优化问题，因此不失一般性的假设 S 是凸的和封闭的。实际上，如果 (2) 中的 S 可能是非凸的或非封闭的，那么用其封闭的凸包替换 S 不会改变最优值 z ∗© (Jaggi 中的引理 8 (2011))。因此，线性优化问题的这种基本等价性意味着我们的方法可以应用于组合和混合整数优化问题，我们将在 3.2 节中进一步阐述。由于假设 S 是固定的并且是确定的，每个问题实例都可以用相应的成本向量来描述，因此依赖于 (2) 中的 c。在求解 c 未知的特定实例时，将改为使用 c 的预测。我们假设可以访问一个实际上有效的优化预言机 w ∗ ©，它为任何输入成本向量返回 P© 的解决方案。例如，如果 (2) 对应于线性、圆锥或混合整数优化问题，那么商业优化求解器或专门的算法就足以满足 w ∗（C）。

2.形式为 (x1, c1),(x2, c2), 的训练数据。. .,(xn, cn)，其中 xi ∈ X 是表示与 ci 关联的上下文信息的特征向量。

的成本矢量预测模型
3.一种假说H级F：X → [R d，其中c ：= F（X）被解释为与特征矢量x关联的预测成本矢量。

4.一种损失函数ℓ （· ，· ）：R d × [R d → R +，由此ℓ （C，C）量化在使预测c中的误差时所实现的（真