电子电路：电流镜电路

电流镜电路可以创造一个很好的温度补偿电流源，常被用于集成电路设计中。
本电路所有的晶体管都是用同一块硅同时制作的，因此，他们拥有共同的温度特性，这是电路能够有效工作的关键条件
下图是一个电流镜电路：

由于晶体管特性相同，T1上的电压 $V_{BE1}$ 和T2上的电压 $V_{BE2}$ 是相同的，集电极的电流也是相同的
借此，我们可以得到电阻R上的电流
$$I_{ref}=\frac{V_{CC}-V_{BE}}{R}$$
根据KCL：
$$I_{ref}=I_O+2I_B=I_O+2\frac{I_O}{\beta }$$
如果$\beta$足够大，则
$$I_O=\frac{I_{ref}}{1+2/\beta }\approx I_{bef}$$

本电路中的$I_{ref}$很大程度上是由$R$决定的，这个电流可以被“镜像后”作为T2的$I_O$

注意如果此时温度改变，两个晶体管的$V_{BE}$都会出现小幅的变化，然而这对R上的电压和$I_{ref}$几乎没有影响，他们保持不变。T1会根据温度有自适应的$V_{BE}$来保证$I_{ref}$不变。因为T1, T2的$V_{BE}$相同，T2所拥有的镜像电流$I_O$也几乎不变

电流镜电路的进阶有电流中继器电路(current repeater circuit)

1. Current repeater circuit

电流中继器电路是由多个镜像晶体管组成的，示意图如下：

这里每个晶体管的电流$I_O$也都是由$I_{ref}$提供的，关系如下：

N即电路中晶体管的数量

这个电路的限制在于，每个负载所产生的电流是相同的，但是有时候我们可能会需要不同的偏置电流
此时可以通过改变晶体管的面积来改变电流，关系如下：

2. Widlar 电流镜

这个电路适用于更大的电流比的环境，它的设计者Widlar有不少有趣的小故事，似乎是一位脾气暴躁的天才，有时间可以了解一下

回归正题，我们还是先看该电路的电路图：

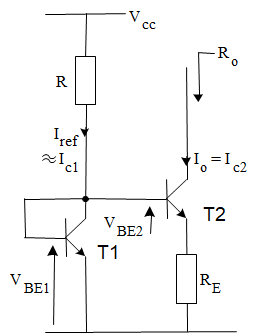
这款电流镜对集成电路内部偏置电流的排布非常有用，主要是因为以下两点：

1. 不同的偏置电流可以通过改变$R_E$来产生，而不用再像传统的电流镜那样改变晶体管的面积
2. 所需的电阻值非常小

这两个特点都可以带来更紧凑的电路设计

2.1 分析

根据晶体管的性质：

接着，我们可以得到晶体管$V_{BE}$的表达式

两者相减，就可以消去漏电流$I_S$，得到：

两者的差还等于电阻$R_E$上的电压：

因此可以得到电阻$R_E$的表达式为：

借此，我们可以通过给出的电流$I_{ref}$和我们想要的输出电流$I_O$求出我们需要的$R_E$的值

接着，我们需要找到电路的输出电阻$R_O$
为此，我们需要找到对于T2集电极的等效电阻$R_o^{\prime }$
从集电极看去的视角如下：

对应的等效电路为：

因此可以得到第一部分输出电阻为：

其中$\frac{1}{g_{m1}}$是电流源的阻抗

为了得到第一部分电流源的有效电阻$r_{e1}=\frac{1}{g_{m1}}$，我们想象给电路注入一个小电流I，如图所示：

有效电阻是电流源上的电压除以上面的电流，即：
$r_e=\frac{v}{i}$
这里的电压等于电阻上的电压：

根据KCL：

那么可以得到$i,v$的表达式为：

最后得到第一部分的输出电阻为：

将这一电阻与电路的第二部分结合，得到：

将$R_O^{\prime }$与电路第二部分的等效电阻结合，假设$r_{\pi 2}>>r_{e1}+R_E$，得到总输出电阻为：

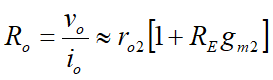
其中$r_{o2}$是第二个三极管的输出电阻
注意，每一个假设我们都需要带入数值对其进行验证
总之，我们可以看到，维德勒电流镜电路的输出电阻是普通晶体管输出电阻的$(1+g_m{R}_E)$倍

注意此时：
？？
其中$R_E{I}_O$是$R_E$上的电压，因为$V_T=0.025V$是一个很小的电压，所以$R_E$上也只需要施加一个不大的电压就可以让电路获得一个非常大的输出电阻$R_O$

实际上，电路中用的两个晶体管是完全相同的，但是由于$R_E$的存在，T2的电流$I_{c2}$将小于$I_{c1}$，这对任何一对拥有合理增益的晶体管都是成立的

3. 带有源负载的差分放大器

在之前差分放大器那一节，我们在技术总结里写明了对电路元件的要求，这里可以重温一下：

1. 为了减小共模电压增益，我们需要增大$R_E$
2. 为了增大差模电压增益，我们需要增大$R_C{I}_{CQ}$（但不能超过$V_{CC}$）
3. 为了增大共模输入阻抗，我们需要增大$R_E,\beta$
4. 为了增大差模输入阻抗，我们需要减小$I_{CQ}$，增大$\beta$

我们已经知道增大$R_E$可以使1和3达到我们想要的效果，那么我们能不能通过增大$R_C$来满足2和4呢？

这里的第一个办法是用电流镜取代$R_C$？？？，效果如下：

但是这会造成一个问题，那就是通过T2的电流与两个独立的电流源有关（T3+T4组成的电流源和$I_S$），这就意味着，如果T3,T4代表的电流$r_{ref}$不能等于$\frac{I_S}{2}$，那么我们就必须要努力改变T2的电流来使得两个电流源能够匹配。
这里的方法之一是在T4和T2之间开一个口让多余的电流离开，如图：

但是这样产生一个额外的电流总归不够体面，最好的解决办法是让T3进入T1的集电极电路，效果如下：

这样做有两个好处：
第一，T3 和 T4的电流是相等的，意味着我们没必要再去匹配两个电流源了，也就不会有额外的电流产生
第二，它可以让电流增益加倍，如果一个输入信号让$v_{i1}$增加$v_{i2}$减少，那么就会引起$I_{C1}$增大，$I_{C2}$减小，$i_{C1}$的减小意味着$I_{C3}$的减小，因为电流镜的缘故，$I_{C4}$也会减小，此时$I_{C4}$与$I_{C2}$的差就会体现在$I_{out}$中，这样输出的电流就是原来$I_{C4}$保持不变时的两倍

将含电流源的T3, T4结合的负载被称为“有源负载”，和$R_C$代表的“无源负载”相对

3.1 电压增益

这种差分放大器的电压增益为:

其中$v_{id}$是差分放大器的得到的电压之差
根据上面得到的输出电流$i_o$，我们可以推出：

为了唱作一个输出电压，输出电流必须流过一个负载，实际中这个负载可以是下一阶段电路的有效输入电阻，假设为$R_L$，那么这个电路的差分电压增益为：

在实际中，T2和T4各自都会有一个输出电阻$r_o$，所以实际中的电压增益会是：

因此为了增大电压增益，应该加大$R_L$
这也说明接入差分放大器输出端的下一阶段的输入电阻会对电压增益起到很大影响
按我个人的理解，下一阶段的输入电阻$R_L$也可以视为$R_E$的一部分，所以他们会对电压增益有类似的影响