周报第六十六周 Snn

week 66 SNN

摘要

本周阅读了题为Efficient and Effective Time-Series Forecasting with Spiking Neural Networks的论文。该文提出了一个在时间序列预测任务中利用snn的框架。通过一系列的实验，证明了提出的基于snn的方法在时间序列预测中的有效性。这些方法在不同的基准数据集上显示出与传统时间序列预测方法相当的性能，同时显著降低了能耗。此外，详细的分析实验揭示了SNN在时间序列数据中捕获时间依赖性的能力。这种见解强调了snn在建模时间序列的复杂动态方面的细微优势和有效性。总之，研究有助于snn领域的扩展，为时间序列预测任务提供了一种节能且生物学上合理的替代方案。

Abstract

This week’s weekly newspaper decodes the paper entitled Efficient and Effective Time-Series Forecasting with Spiking Neural Networks. The paper presents a framework for utilizing SNNs (Spiking Neural Networks) in time series prediction tasks. Through a series of experiments, it demonstrates the effectiveness of the proposed SNN-based approach in time series forecasting. These methods show comparable performance to traditional time series prediction techniques on various benchmark datasets while significantly reducing energy consumption. Furthermore, detailed analytical experiments reveal the capability of SNNs to capture temporal dependencies within time series data. This insight highlights the subtle advantages and effectiveness of SNNs in modeling the complex dynamics of time series. In summary, the research contributes to the expansion of the SNN field, offering an energy-efficient and biologically plausible alternative for time series prediction tasks.

1. 题目

标题：Efficient and Effective Time-Series Forecasting with Spiking Neural Networks

作者：Changze Lv 1 Yansen Wang 2 Dongqi Han 2 Xiaoqing Zheng 1 Xuanjing Huang 1 Dongsheng Li 2

发布：Proceedings of the 41 st International Conference on Machine Learning, Vienna, Austria. PMLR 235, 2024. Copyright 2024 by the author(s).

链接：https://arxiv.org/abs/2402.01533

code：https: //github.com/microsoft/SeqSNN

概述：脉冲神经网络 （SNN） 受到生物神经元脉冲行为的启发，为捕获错综复杂的时间数据提供了独特的途径。然而，由于有效时间对齐的困难、编码过程的复杂性以及缺乏标准化的模型选择指南，将 SNN 应用于时间序列预测具有挑战性

2. Abstract

受生物神经元的尖峰行为启发的尖峰神经网络（snn）为捕获复杂的时间数据提供了一种独特的途径。然而，将snn应用于时间序列预测是具有挑战性的，因为难以有效的时间对齐，编码过程的复杂性，以及缺乏标准的模型选择指南。在本文中，我们提出了一个snn在时间序列预测任务中的框架，利用尖峰神经元处理时间信息的效率。通过一系列实验，我们证明了我们提出的基于snn的方法在不同基准上取得了与传统时间序列预测方法相当或更好的结果，并且能耗更低。此外，我们进行了详细的分析实验，以评估SNN在时间序列数据中捕获时间依赖性的能力，为其在模拟时间数据复杂动态方面的细微优势和有效性提供有价值的见解。我们的研究有助于snn领域的扩展，并为时间序列预测任务提供了一个有希望的替代方案，为开发更具生物学启发和时间感知的预测模型提供了一条途径。

3. 文献解读

3.1 Introduction

在本文中，我们提出了一个snn在时间序列预测任务中的框架。首先，利用尖峰神经元处理时间序列信息的效率，我们成功地对齐了时间序列数据和snn之间的时间步长。其次，我们设计了两种类型的编码层，将连续时间序列数据转换为有意义的尖峰序列。我们在4个广泛使用的时间序列预测基准上对我们提出的SNN模型进行了综合评估，结果表明SNN在能量消耗更少的情况下取得了与经典ann相当甚至更好的结果。此外，我们进行了分析实验，以展示snn如何捕获时间序列数据中的时间依赖性，并发现snn确实可以模拟时间序列数据的内部动态。

3.2 创新点

本研究的主要贡献如下：

1. 框架。我们提出了SNN在时间序列预测任务中的统一框架，包括时间序列数据编码和SNN模型架构，该框架为时间序列预测提供了一种节能且生物可行的替代方案。
2. 表现。所提出的框架使SNN域的性能能够达到与现有经典ANN基线相当甚至更好的性能，而能耗要低得多。深刻的分析。
3. 据我们所知，本文是第一批提供全面分析的论文之一，包括模型级调查和时间分析，研究snn如何成功捕获时间序列数据中的特征。

4. 网络结构

4.1 基础

4.1.1 任务定义

我们考虑常规时间序列预测任务，其中所有时间序列都是从底层连续信号X(t)中采样的序列，离散步长∆t为$x_k=\mathcal{X}(k∆t)$。给定历史观测到的时间序列 X = { x 1 , x 2 ， … ， x T } ∈ R T × C \mathbf X = \{x_1, x_2，\dots， x_T\}\in \mathbb R^{T×C} X={x1​,x2​，…，xT​}∈RT×C对于T个时间步长，多元时间序列预测任务旨在预测后续L个时间步长的值 Y = { x T + 1 , x T + 2 , … , x T + L } ∈ R L × C \mathbf Y = \{x_{T+1}, x_{T+2}, \dots, x_{T+L}\}\in \mathbb R^{L×C} Y={xT+1​,xT+2​,…,xT+L​}∈RL×C，其中C为变量个数。

4.1.2 刺激神经元和替代梯度

snn的基本单元是漏集成点火（LIF）神经元（Maass, 1997），它在输入电流I(t)下工作，并在时间t时产生膜电位U(t)和尖峰S(t)。图1所示LIF神经元的动力学可以写成：
$$U(t)=H(t-\Delta t)+I(t),I(t)=f(\text{x};\theta )\text{\hspace{1em}(1)}$$

$$H(t)=V_{reset}S(t)+(1-S(t))\beta U(t)\text{\hspace{1em}(2)}$$

$$S(t)=\{\begin{array}{l}1,\text{if}U(t)\ge U_{thr},\\ 0,\text{if}U(t)<U_{thr}\end{array}\text{\hspace{1em}(3)}$$

其中I(t)是LIF神经元在时间步长t处的空间输入，通过应用函数f以x为输入，θ为可学习参数计算。H(t)是神经元在时间步长t的时间输出，∆t是控制LIF建模粒度的离散化常数。脉冲S(t)被定义为依赖于膜电位的Heaviside阶跃函数。当U(t)达到阈值Uthr时，神经元将放电并发出一个尖峰，然后时间输出H(t)将重置为Vreset。否则，膜电位U(t)将衰减为H(t)，衰减速率为β。

现在我们生成尖峰序列$\mathbf{S}\in {\mathbb{R}}^{T^{\prime }\times N}$，尖峰神经元层$\mathcal{S}\mathcal{N}(\cdot )$：
$$\mathbf{S}=\mathcal{S}N(\mathbf{I})\text{\hspace{1em}(4)}$$
选择使用代理梯度的直接训练作为训练snn的方法。参照Fang et al. (2020b)，选择类arcarcant代理梯度作为反向传播时的误差估计函数，将Heaviside阶跃函数（式3）视为：

$$\begin{array}{c}S(t)\approx \frac{1}{\pi }\arctan \left(\frac{\pi }{2}\alpha U(t)\right)+\frac{1}{2}\end{array}\text{\hspace{1em}(5)}$$
其中α是控制arctan函数频率的超参数。因此，方程5中S的梯度为 $\frac{\partial S(t)}{\partial U(t)}=\frac{\alpha }{2}\frac{1}{\left(1+{\left(\frac{\pi }{2}\alpha U(t)\right)}^2\right)}$，因此整个模型可以通过时间反向传播（BPTT）以端到端方式训练。

4.2 时域校准和尖峰编码器

4.1.3 即时反应模式

为了最大限度地利用SNN的固有特性，在时间序列数据和SNN之间对齐时间维度是至关重要的。我们的核心概念是在每个时间步长中合并时间序列数据中峰值的相关精细信息。具体来说，我们将时间序列的一个时间步长∆T划分为Ts段，每一段都允许膜电位超过阈值的神经元发生放电事件，即$∆T=T_s∆t$。

这个方程连接了时间序列时间步长∆T和SNN时间步长∆T。因此，时间序列 $(\mathcal{X}(t))$中的自变量t和SNN $(\mathcal{X}(t))$​中的自变量t现在具有相同的含义。为此，负责根据浮点输入产生第一个尖峰序列的尖峰编码器需要计算Ts × T × C可能的尖峰事件。最直接的非参数方法是将输入时间序列中的每个数据点视为当前值，并将其复制t次。然而，这种方法可能会破坏底层X(t)假设的连续性。因此，我们寻求使用参数尖峰编码技术。

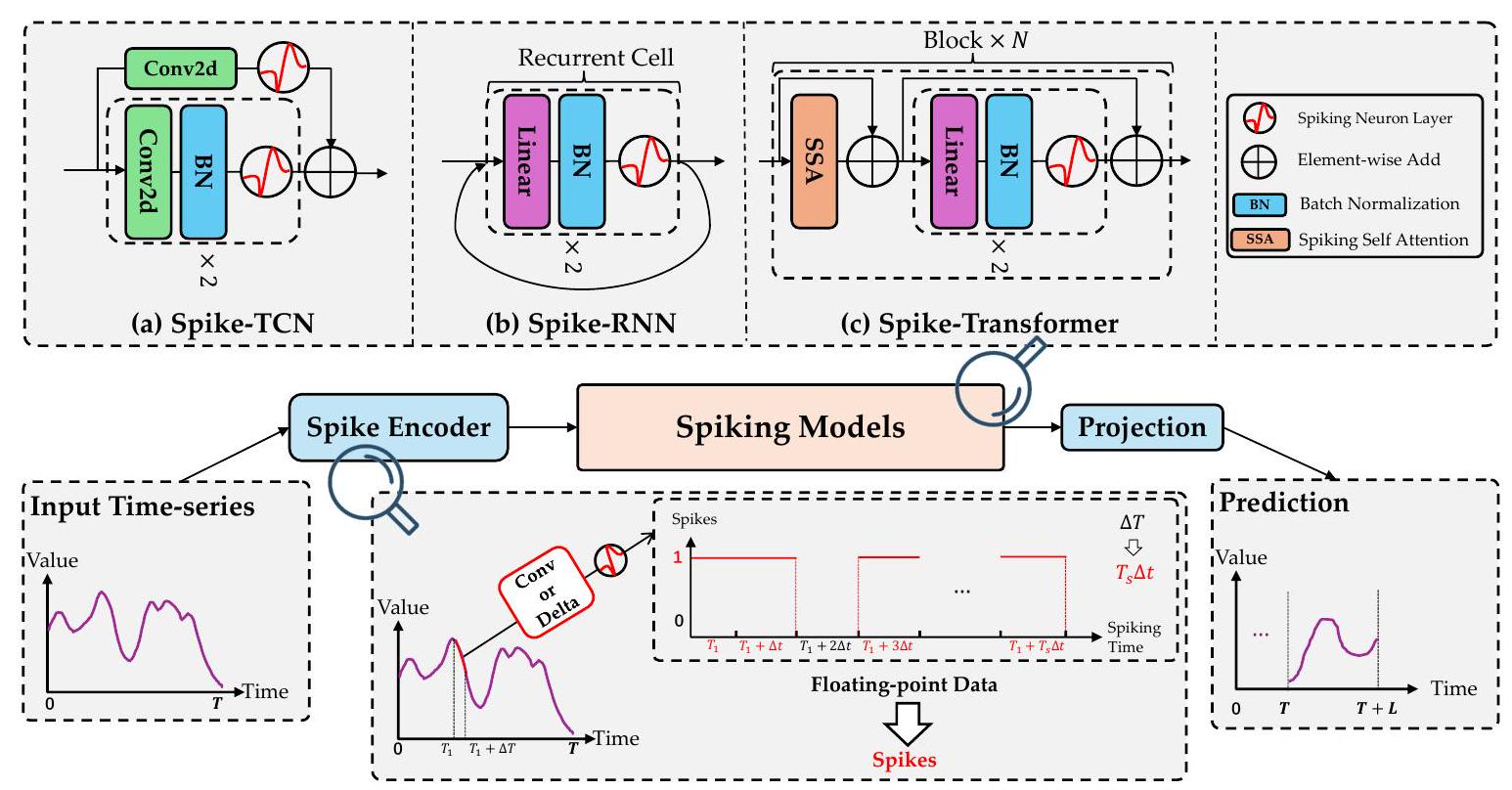
Delta Spike Encoder 源于Delta调制（Eshraghian et al., 2021），灵感来自于神经元对时间变化敏感的生物学概念。控制这个过程的数学表达式封装如下：
$$\begin{array}{c}\mathbf{S}=\mathcal{S}\mathcal{N}\left(\mathrm{BN}\left(\text{ Linear }\left({\mathbf{x}}_t-{\mathbf{x}}_{t-1}\right)\right)\right)\end{array}\text{\hspace{1em}(6)}$$
其中，对时间差施加线性层，学习不同SNN时间步长的不同灵敏度，并将尖峰序列的维数S扩展为Ts × T × c。结果经过批归一化（batch normalization， BN），通过尖峰神经元层SN转换为尖峰序列。

Convolutional Spike Encoder 在时间序列任务中，序列的形状通常被归类为可解释的特征（Ye & Keogh, 2009），用于时间序列分类和聚类。最近，Qu等人（2024）证明了这种形态信息可以通过一种特定类型的CNN核来建模。因此，我们建议使用卷积层作为合适的时间编码器，只要原始子序列的形状与核匹配，它就会发出尖峰。

给定历史观测到的时间序列$\mathbf{X}\in {\mathbb{R}}^{T\times C}$，我们将其送入卷积层，然后进行批处理归一化，并生成峰值如下：
$$\begin{array}{c}\mathbf{S}=\mathcal{S}\mathcal{N}(\mathrm{BN}(\mathrm{Conv}(\mathbf{X})))\end{array}\text{\hspace{1em}(7)}$$
与delta尖峰编码器类似，通过卷积层，尖峰序列S的维度扩展到$T_s\times T\times C$。每个SNN时间步长的峰值是通过将数据与不同的卷积核配对来产生的。

delta尖峰编码器和卷积尖峰编码器分别捕获输入数据的内部时间信息，即时间变化和形状，有助于表示信息随时间的动态性质，并满足事件驱动建模的以下尖峰层。

4.3 Spiking Model Architrcture

Spike-TCN Temporal Convolutional Network (TCN) （Bai et al., 2018）使用卷积核对时间序列进行建模。与一般的cnn不同，TCN可以将任意长度的时间序列映射到相同的长度，而不会从未来到过去的信息泄漏。受图像分类实践的启发（He et al., 2016），最近的TCN也引入残差连接来克服梯度不稳定问题。

继Hu et al.（2018）之后，我们通过对原始TCN进行以下更改来构建Spike-TCN: 1)我们将ReLU激活函数替换为spike神经元层。这种替代是snn的一个特征，在snn中，神经元的放电以一种生物学上更合理的方式模拟。2)我们去掉了对硬件不友好的dropout操作。dropout操作包括两个步骤：以p的概率随机将输入张量的一些元素归零，并将输出按 $\frac{1}{1-p}$的因子进行缩放。第二步介绍了除法操作，这不是硬件友好的。3)我们用spikeelement-wise （SEW）残差模块（Fang et al., 2021）取代了香草TCN中的残差快捷方式，该模块实现了身份映射并克服了spiking版本中的消失/爆炸梯度问题。4)降采样模块也转换为峰值版本，遵循SEW规则。

由于TCN只涉及局部卷积，不跨时间步长跟踪时间状态，因此在每个时间序列时间步长开始时，Spike-TCN中的膜电位U(t)设为0。这使得并行训练成为可能。

Spike-RNN 普通递归神经网络（RNN）使用其内部状态来处理输入序列，并可以迭代输出相同长度的序列。我们用尖峰神经元层代替激活函数，将原始RNN的循环单元重写为尖峰-RNN。与TCN不同，RNN跟踪时间状态，因此SpikeRNN中的膜电位将在时间步长中持续存在。我们还修改了门控循环单元（GRU） （Cho等人，2014），这是RNN的一种流行变体，它使用门控机制来解决长期依赖问题。

Spike-Transformer 在时间序列预测任务中使用Transformer架构吸引了大量关注(Wu et al., 2021；Liu et al., 2024)，但对于应用自注意操作的最佳框架尚未达成共识。在这项工作中，我们基于ittransformer （Liu et al., 2024）构建了我们的峰值版本Transformer，并将其命名为“iSpikformer”，考虑到两个理由：1)ittransformer是几个公共基准上最先进的时间序列预测模型，因此足够强大，可以作为我们的基础；2) iTransformer将独立的时间序列作为标记，通过自关注机制捕获多变量相关性，主要关注跨通道的空间建模。通过构建其峰值对应物，我们证明了我们的峰值设计来模拟时间动力学本质上与空间建模是正交的，并且可以通过相关的进步进一步推进。

目前，有各种为图像分类任务设计的峰值变压器(Li et al., 2022；周等，20023b；Yao et al., 2023a)。其中，基于Spikformer的Spikformer v2 （Zhou et al., 2024）在Imagenet-1k和CIFAR-10基准上实现了当前最先进的性能。因此，我们遵循Spikformer实现了spike自关注（SSA）机制，并使用它来取代ittransformer中原始的自关注层来构建我们的Spikformer模块。

具体来说，在第3.2节详细介绍的尖峰编码器获得尖峰列后，将应用一个通道级的尖峰嵌入层：
$$\begin{array}{c}{\mathbf{S}}_{emb}=\mathcal{S}\mathcal{N}(\text{ Linear }(\mathbf{S}))\end{array}\text{\hspace{1em}(8)}$$
其中${\mathbf{S}}_{emb}\in {\mathbb{R}}^{H\times C}$是尺寸为h的C通道方向嵌入，这些嵌入随后被馈送到峰值变压器块中。

请注意，我们为时间序列预测设计的snn严格遵守硬件友好要求。具体来说，该模型的推理过程避免了涉及浮点运算，如乘法累加（MAC）运算。这种设计选择使这些模型能够有效地部署在神经形态芯片上，符合此类平台的硬件限制和特点。

4.4 . Spike Decoding

经过最后的峰值神经元层后，我们得到了用${\mathbf{S}}_{\text{hidden }}$表示的峰值隐藏状态。在图像分类任务中，通常使用线性层作为分类头来进行预测。类似地，在时间序列预测的上下文中，这本质上是一个回归任务，我们通过应用一个全连接层（表示为$\mathbf{Y}=\mathrm{Linear}\left({\mathbf{S}}_{\text{hidden }}\right)$）将峰值数据转换为预测序列。由于在此步骤之后没有对$\mathbf{Y}$​应用额外的浮点操作，因此可以将其容纳在我们的设计框架中。

5. 实验过程

数据集

为了评估比较方法的预测能力，使用了以下列出的数据集：meter -la (Li et al., 2017b)：在洛杉矶县高速公路上测量的平均交通速度；Pems-bay (Li et al., 2017b)：湾区平均交通速度；电力（Lai et al., 2018）：以千瓦时为单位的小时用电量；太阳能（Lai et al., 2018）：太阳能发电记录。

基线

在这些预测数据集上，我们将我们的方法与两种统计方法ARIMA （Box等人，2015）和GP （Roberts等人，2013）进行比较；一个基于cnn的模型TCN (Bai et al., 2018)；一个基于rnn的模型GRU (Cho et al., 2014)；两个基于Transformer的模型Autoformer （Wu et al., 2021）和itransformer （Liu et al., 2024）。

为了评估时间序列预测任务，我们采用了根相对平方误差（RSE）和决定系数（R2）。数据集的详细统计、模型的超参数和评价指标的制定可参考附录A。

实验结果

我们在表1中报告了所有方法在4个不同预测长度L的时间序列预测任务上的结果。ARIMA、GP、GRU和Autoformer的结果来自Fang等人（2023）的研究。

从表1中可以得出结论，所有snn都成功地对时间序列进行了建模，并取得了合理的性能，我们的iSpikformer与最先进的ANN模型相比取得了相当甚至更好的性能

(1)当时间动态得到适当的保存和处理时，snn会成功。虽然Spike-TCN表现不如TCN，但Spike-GRU和Spike-RNN在GRU基线上取得了明显更好的性能。我们将这种现象归因于模型处理顺序动力学的不同能力。与TCN类似，Spike-TCN只对序列的局部特征进行建模，而不跟踪时序状态。因此，膜电位很难在时间步长上重置为0，这违背了snn的性质。另一方面，Spike-RNN和SpikeGRU坚持这种时间信息，并迎合我们整体的事件驱动范式。值得强调的是，Spike-RNN可以在长期和短期历史观察的基准测试中获得最先进的性能。此外，通过检查图3中描述的关键差异图，我们可以将我们使用的所有方法大致分为三个层次，并且令人惊喜的是，我们的iSpikformer排在顶层。

(2)基于时间建模的snn可以通过先进的空间建模技术进一步改进。我们的研究中最突出的发现之一是iSpikformer的卓越性能，其结果与最先进的人工神经网络模型ittransformer几乎没有区别。从表1中可以看出，与所有其他方法相比，iSpikformer的平均RSE最低，其R2性能与iTransformer基本匹配，仅边际下降0.001。此外，值得注意的是，iSpikformer的RSE在所有基准数据集中一直是最低或第二低的。这些发现证实，我们的时间建模技术完美地补充了最先进的空间建模技术，并且脉冲神经网络可以非常有效地解决一般的时间序列预测任务。